基于粗糙集的网络化防空节点重要度评估*

（海军航空大学 烟台 264001）

1 引言

网络化防空系统的建设是防空系统在未来一体化防空作战建设中的重点和方向，由于防空系统是由众多作战节点组成的复杂作战系统，且各作战节点在防空系统中的重要程度是不相同的，因此合理排列出节点的重要度，对提高防空系统生存能力和可靠性具有重要作用［1］。

现阶段公认的重要度或价值分析方法主要从节点自身价值和整体价值两个方面入手，通过某一特定算法加以结合，得出比较正确的结论。这种算法虽然结构清晰、浅显易懂，但相比较于基于粗糙集的综合评价方法还是显得过于复杂。基于粗糙集的综合评价方法是根据观测数据删除冗余信息，比较不完整知识的程度（粗糙度）、属性间的依赖性与重要性，从而导出问题决策和分类规则［2］。因此，本文采用将网络节点自身价值属性和整体价值属性结合为同一的节点属性的方式，通过基于粗糙集的综合评价方法对网络化防空节点重要度进行排序。

2 网络化防空节点重要度分析

网络化防空作战是网络中心战在防空作战领域的具体应用，是由各防空节点通过网络实现共享，大幅提高作战效能的一种作战样式。防空节点通常包括预警探测节点、指挥引导节点、火力打击节点以及电子对抗节点等［3］，因此，一个网络化防空系统描述可如图1所示。连线表示各节点间的物理、逻辑联系。

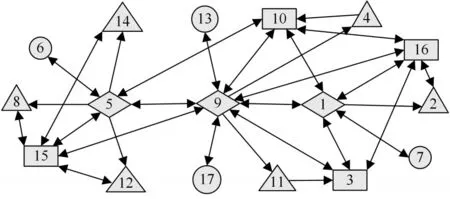
图1 网络化防空系统结构图

防空节点重要度是指该节点会对实现我方作战目标的贡献程度和对敌方的威胁程度［4］。不同的节点有不同的重要度，主要包含以下几个因素，如图2所示。

图2 属性重要度评估体系

1）对敌威胁程度。指该防空节点对防御目标袭击成功的概率及成功时所造成毁伤的大小，是敌对我防空节点重要度排序的重要依据。通常来说，对敌威胁程度越大，遭受攻击的可能性就越大，反之则越小。

2）对我作战影响。防空节点的种类包括预警、指挥、打击、电子对抗、后勤等，由于各自功能的不同，对我作战的影响也有很大的不同，可以通过节点在整个作战系统中的作用来判断影响大小。

3）与作战意图一致度。防空节点功能与作战意图一致度越高，该节点在作战中发挥的作用就越大，重要度就越高。

4）抗毁能力。防空节点的抗毁能力直接影响它的重要度。通常来说，防空节点的抗毁能力越强，所需要的防护就越弱，重要度就越低，反之则越大。

5）修复难度。修复能力是保证防空系统持续作战能力大小的关键因素，防空节点被毁伤或失效时，其修复难度的大小直接决定着该防空节点的重要度。这里把修复难度划分为强、中、弱、无4个等级。

6）节点连通数。节点连通数是衡量节点与其他节点相联系的数量。节点连通数以节点与其他节点连通的数据流通方向为依据，连通数量越大，节点在网络中越活跃。

7）节点关键度。节点关键度是衡量节点在防空体系网络结构中地位的测度。如防空体系网络结构中的“非中心节点”和“中心节点”的关键程度是不一样的［5］。节点关键度以节点到其他节点的最短路径长度为指标，最短路径长度越小，节点关键度越大，节点在网络结构中的地位越重要。假定t(ui，uj)表示以节点ui为起点，节点uj为终点的最短路径长度，则节点ui的关键度为

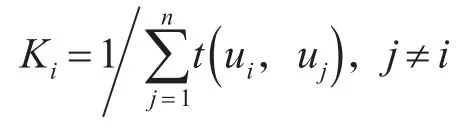
3 基于粗糙集的节点重要度评估模型与步骤

粗糙集理论是一种处理模糊性和不确定性的数学方法，它直接从给定问题的描述集合出发，通过不可分辨关系和不可分辨类确定给定问题的近似域，从而找出该问题的内在规律［6］。

在粗糙集理论中［2，6～7］，知识被认为能够对研究对象进行分类。设一个知识表达系统，S=(U，R，V，f)，U表示研究对象组成的非空有限集合，称为论域；R=C∪D表示能对U进行等价划分的属性非空有限集合，称为知识，C和D分别表示条件属性集和决策属性集；V表示属性值集合，Vr表示属性r∈R的值域；f表示U中每个对象的属性值，是一个信息函数。

假设网络化防空系统有n个节点，有k条链路，每个节点有m个属性，用U={u1，u2，…，un}表示节点集合，C={c1，c2，…，cm} 表示节点属性集合。

3.1 建立关系数据模型

将每个属性评价指标视为条件属性，则条件属性集合为C={c1，c2，…，cm} ，每个节点在各项属性评价指标上的取值视为该节点的一条信息，ui={vi1，vi2，…，vim} ，论域U={u1，u2，…，un} 为所有节点的集合。这时节点ut的属性值vj(ut)=vtj，其中j=1，2，…，m；t=1，2，…，n，则由ut构成的二维信息表S=(U，R，V，f)就是所要建立的关系数据模型，见表1。

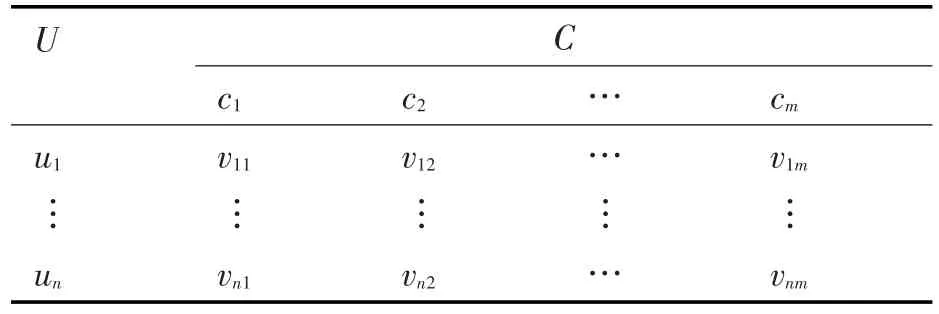
表1 节点重要度评估信息表

3.2 属性指标量化及体系缩减

属性指标有定性指标和定量指标［8］。定性指标量化的方法有专家评分法［9］和两级比例标度法［10］等；定量指标量化的方法有区间数表示法［11］、区间量化法［12］和模糊数表示法［13］等。运用粗糙集理论进行评价时，信息表中的数值必须用离散数据表达，如果某值域为连续值，则必须进行离散化处理。属性离散化算法有等距离划分算法、等频率划分算法等［2］。

在量化信息表后，如果存在属性i、j对应的评价对象的属性值相同，则认为i、j在现行规则下无区别、是重复的，删除重复列，缩减指标体系。

3.3 确定指标权重

确定指标权重的基本思路是从信息表中去掉某一属性来考查各属性的分类变化，从而得出指标权重。其步骤为

步骤1：计算决策属性指标D对属性指标集合C的依赖程度。

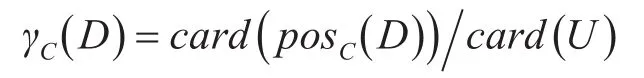
其中，card(U)表示集合U中元素的数量，posC(D)表示D相对于C的正域。

步骤2：对每个属性指标cj，计算决策指标D对属性指标集合C-{cj}的依赖程度，j=1，2，…，m。

步骤3：计算第j种属性指标的重要性。

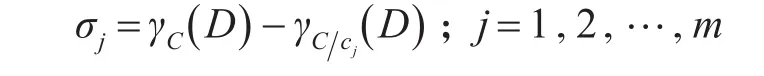
步骤4：归一化处理，计算出第j种属性指标的权重。

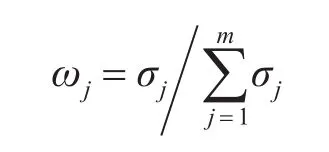
3.4 综合评价计算

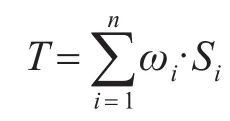
4 实例应用

运用粗糙集理论对网络化防空节点重要度评估是一种可行的方法，为了验证这种方法是否可靠、有效，在数据选取方面，既要符合网络化防空作战实际，又要不失一般性。

1）建立关系数据模型。以图1所示的网络化防空系统为例，分析其节点重要度，假定防空系统中各节点的重要度属性值如表2所示。设定条件属性C={c1对敌威胁程度；c2对我作战影响；c3与作战意图一致度；c4抗毁能力；c5修复难度；c6节点连通数；c7节点关键度}。

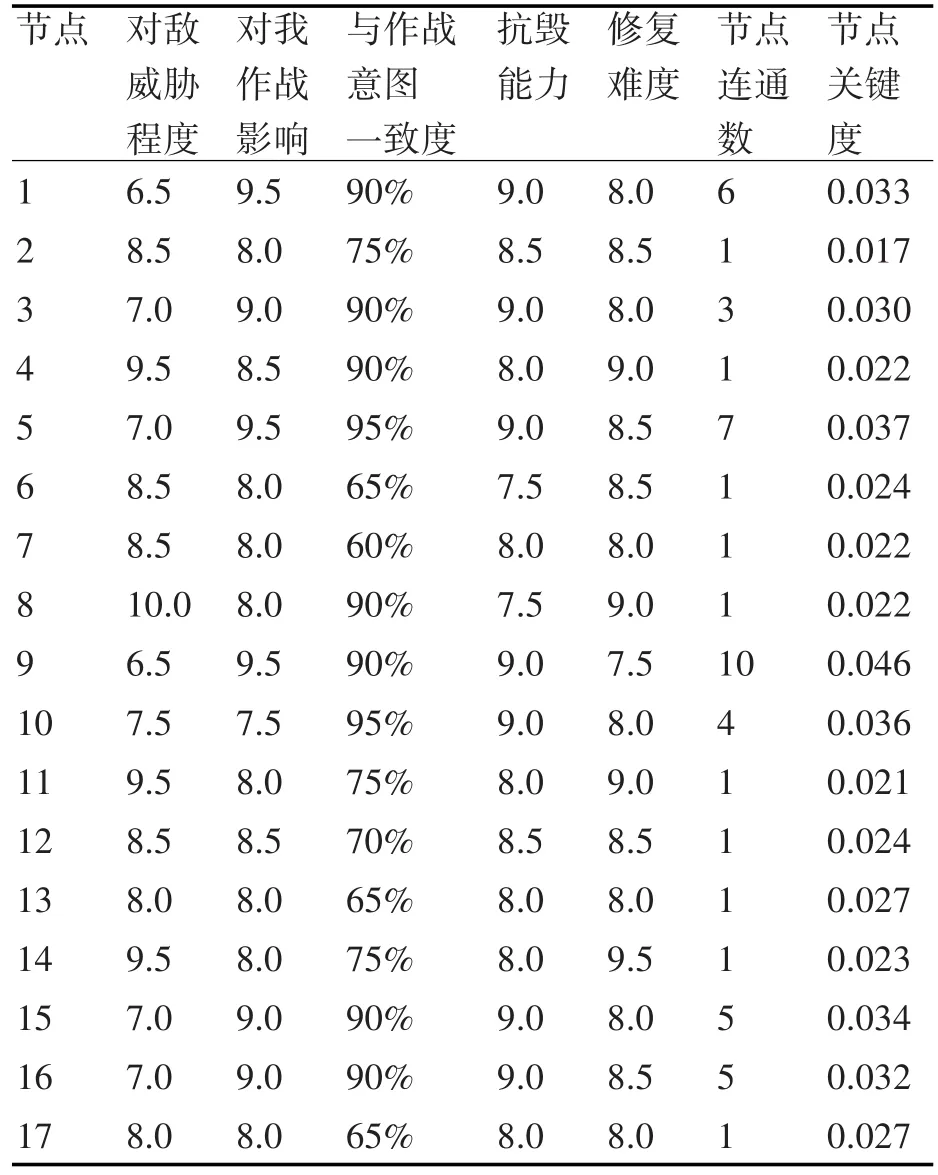
表2 网络化防空节点的属性值

2）属性指标量化及体系缩减。对表2中各指标属性进行离散化处理。

根据上述分段，对防空节点的属性值进行离散化处理，得表3知识表达系统。

表3 网络化防空节点各属性量化值

由表3可得出：第13和17节点属性量化值完全相同，属于重复行，则可对表3进行缩减，得知识表达系统简化表，如表4所示。

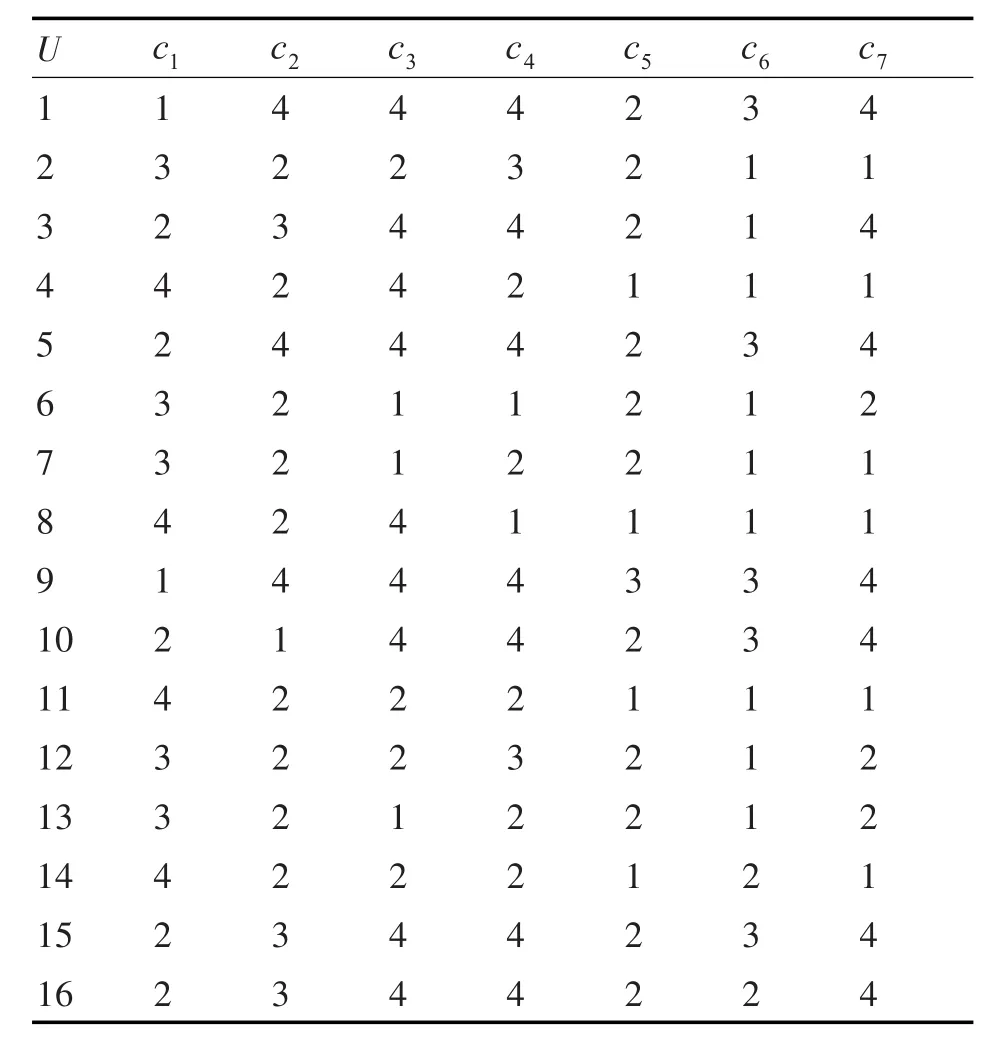
表4 网络化防空节点各属性量化值简化表

3）确定指标权重。由表4可以得到：

U/ind(C)={(1)，(2)，(3)，(4)，(5)，(6)，(7)，(8)，(9)，(10)，(11)，(12)，(13)，(14)，(15)，(16)}

U/ind(C-c1)={(1， 5)，(2)，(3)，(4)，(6)，(7)，(8)，(9)，(10)，(11)，(12)，(13)，(14)，(15)，(16)}

U/ind(C-c2)={(1)，(2)，(3)，(4)，(5， 10， 15)，(6)，(7)，(8)，(9)，(11)，(12)，(13)，(14)，(15)，(16)}

U/ind(C-c3)={(1)，(2)，(3)，(4， 11)，(5)，(6)，(7)，(8)，(9)，(10)，(12)，(13)，(14)，(15)，(16)}

U/ind(C-c4)={(1)，(2)，(3)，(4， 8)，(5)，(6， 13)，(7)，(9)，(10)，(11)，(12)，(14)，(15)，(16)}

U/ind(C-c5)={(1，9)，(2)，(3)，(4)，(5)，(6， 13)，(7)，(8)，(10)，(11)，(12)，(13)，(14)，(15)，(16)}

U/ind(C-c6)={(1)，(2)，(3， 15，16)，(4)，(5)，(6)，(7)，(8)，(9)，(10)，(11， 14)，(12)，(13)}

U/ind(C-c7)={(1)，(2，12)，(3)，(4)，(5)，(6)，(7，13)，(8)，(9)，(10)，(11)，(14)，(15)，(16)}

从而可以得到：

posC(f)={1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}=16;

pos(C-c1)(f)={2，3，4，5，6，7，8，9，10，11，12，13，14，15，16}=14;

pos(C-c2)(f)={1，2，3，4，5，6，7，8，9，11，12，13，14，15，16}=13;

pos(C-c3)(f)={1，2，3，5，6，7，8，9，10，12，13，14，15，16}=14;

pos(C-c4)(f)={1，2，3，5，7，9，10，11，12，13，14，15，16}=12;

pos(C-c5)(f)={2，3，4，5，6，7，8，10，11，12，13，14，15，16}=14;

pos(C-c6)(f)={1，2，4，5，6，7，8，9，10，12，13}=11;

pos(C-c7)(f)={1，3，4，5，6，8，9，10，11，14，15，16}=12。

进而可以求得：

γC(D)=16/16=1;

γ(C-c1)(f)=14/16=0.875，qc1=1-0.875=0.125;

γ(C-c2)(f)=13/16=0.8125，qc1=1-0.8125=0.1875;

γ(C-c3)(f)=14/16=0.875，qc1=1-0.875=0.125;

γ(C-c4)(f)=12/16=0.75，qc1=1-0.75=0.25;

γ(C-c5)(f)=14/16=0.875，qc1=1-0.875=0.125;

γ(C-c6)(f)=11/16=0.6875，qc1=1-0.6875=0.3125;

γ(C-c7)(f)=12/16=0.75，qc1=1-0.75=0.25。

经过归一化处理，可分别得到各指标的权重为ωi=(0.091，0.136，0.091，0.182，0.091，0.227，0.182)

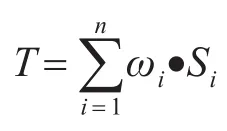
5 结语

网络化防空节点重要度评估排序问题是未来防空作战中兵力部署的一个核心问题。本文提出了基于粗糙集的节点重要度评估方法，简化了传统的“自身—整体—再结合”的评估方法，提高了评估的时效性，更符合未来战场实际情况，可为指挥员更快速进行指挥决策提供参考。