三维随机粗糙海面与舰船的复合电磁特性的高频方法分析研究
何 姿 陈如山
(南京理工大学电光学院 南京 210094)
1 引言
实现粗糙面上方目标的电磁散射特性的快速分析在低空飞行器识别与监测、微波遥感以及雷达制导等领域有重要的研究意义。为了简化模型的计算,通常将背景(例如海洋、草地及沙漠等)和散射目标(例如飞机、舰船及导弹等)分为两个独立的部分进行计算,因此散射目标和背景之间的影响不能够被考虑在内。
对于2维随机粗糙面模型的建立,除了可以使用入射波波长来衡量随机粗糙面的粗糙程度,还可以使用其它统计量来描述,例如均方根高度、相关函数和表面相关长度、功率谱密度、均方根斜率等等。由于2维随机粗糙面的电尺寸大,很难使用全波分析方法进行仿真与计算,因此,很多学者都是在一定的假定条件下得出近似解。基尔霍夫近似方法(KA)[1,2]是计算粗糙表面电磁散射问题的最为常见的一种近似方法,它认为粗糙面上任意一点的场强都可以由这一点上的切平面反射波来确定,因此,粗糙表面上任意一点的总场可近似为入射场与这点处相切的无穷大平面的反射场之和。微扰法(SPM)[3,4]中可将散射场近似等效为由远离边界而传播的不同振幅的平面波相加而成,这种方法只适用于小尺度的表面高度波动情况比入射波波长小和均方根斜率远远小于1的情形。小斜率近似方法(SSA)[5,6]相对于上面两种方法,使用范围更加广泛,并且对于大角度入射的时候,计算精度也相对比较高。除此之外,常见的近似方法还有双尺度法(Two Scale Model, TSM)[7]、消光定理(Extinction Theorem, ET)[8]、全波法(Full Wave Algorithm,FWA)[9]以及相位微扰法(Phase Perturbation Technique, PPT)[10]等。以上几种方法虽然计算速度快,占用内存小,但是没有考虑目标各个单元之间的互耦以及目标的边缘绕射和电磁波的多径传播。因此,开发有效的数值仿真方法分析这类问题是非常必要和急迫的。全波数值仿真方法主要有积分方程方法[11]和微分方程方法[12,13],它们可以精确地求解麦克斯韦方程,并求得空间的电磁场分布,但是,随着目标的电尺寸的增加,全波数值仿真方法所需要的计算资源也会剧烈地增长,因此不能够有效地分析大型的随机粗糙面。今年,很多学者开发出了一些快速算法来加速随机粗糙海平面与其上方物体电磁散射的快速建模分析[14–20],例如广义前后向迭代法(GFBM)[14],广义前后向算法与谱加速方法(GFBM/SAA)[15],二次弹射法[16],基于KA分析的快速多级子方法(KA-MLFMA)[17]等方法,进一步降低了计算资源的消耗。
同期,国内的许多学者分别采用多种数值方法,系统地开展了海面等粗糙面与目标复合的电磁散射特性研究。金亚秋等人采用双向解析射线追踪(BART)算法、FBM和共轭梯度法(CG)相结合的快速互耦迭代混合算法(FBM-CG)、FBM和扩展传播内层展开(EPILE)混合算法、KA和MoM相结合的混合算法(KA-MoM)等技术计算了舰船目标与粗糙海面的复合散射[21]。郭立新等人研究了物理光学近似,以及时频域数值混合算法分析了目标与粗糙面复合散射问题[22]。康士峰等人应用矩量法研究了粗糙面与其上方目标的散射回波特征[23]。朱国强等人基于物理光学法的双次弹射法、多层UV分解法以及利用谱域积分和高频近似混合算法分析了粗糙面上目标的电磁波复合散射[24]。童创明等人提出一种快速精确求解复杂陆地粗糙面及其上方坦克目标复合散射的混合方法[25]。盛新庆等人提出基尔霍夫近似结合多层快速多极子技术研究1维介质粗糙面与上方目标的后向散射[26]。许小剑等人采用混合高频方法研究了海面与目标形成的角反射器结构,建立了时变海面舰船目标动态雷达特征信号的数值仿真模型[27]。张民等人运用时域表面积分方程方法研究了锥形波入射下粗糙海面和3维介质目标的瞬时散射特征,并基于结合小面元模型的多路径复合散射理论、IPO-MEC等算法广泛开展了海上目标电磁环境建模及SAR成像仿真工作[28]。陈如山等人基于矩量法,采用特征基函数(CBF)结合矩阵分解算法(MDA),以及谱预条件技术实现粗糙面目标电磁散射特性快速分析[29,30]。市场上主流的电磁仿真商用软件有FEKO, HFSS, CST以及FDTD Solutions等,但是这些软件的核心代码被国外垄断,价格偏高,可拓展性差,因此,仍需要开发更为有效的数值计算方法用于分析海上目标电磁散射问题。
本文从高频近似方法出发,分别介绍了物理光学方法(PO)、迭代物理光学方法(IPO)以及PO-IPO混合方法,实现了3维随机粗糙海平面及其上方物体一体化建模与电磁散射特性的分析。可以看出,PO方法的计算速度最快,IPO方法相对于PO方法,当分析结构较为复杂的物体时,计算精度得到显著的提高,但是计算效率会有所降低。因此,本文采用PO-IPO的混合方法,使用IPO分析粗糙海面上方的物体,考虑到粗糙面上方物体的互耦作用,使用PO分析海面以及海面与物体间的作用,从而能够有效地对3维随机粗糙海面与舰船的复合目标的电磁散射特性进行分析。
2 原理介绍
2.1 物理光学方法(PO)原理
当物体接受到电磁波的照射时,物体表面就会感应出电磁流,从而可以获得远区的散射场。物理光学方法不考虑单元之间的互耦,因此不需要求解矩阵方程,因此计算效率高,在工程中有很强的实用性。由Stratton-Chu公式,可得到散射场公式如下

2.2 迭代物理光学方法(IPO)原理
物理光学方法不考虑各个面元之间的耦合作用,可以将各个面元视为单独的辐射单元。因此,物理光学方法可以较为有效地分析电大简单的模型,但是,对于含有强耦合结构的散射体,物理光学方法就不能够满足计算精度的要求。1995年,Feamndo Obelleiro-Basteiro, Jose Luis Rodriguez和Robert J.Burkholder等人首次提出了利用迭代物理光学法分析含腔物体的电磁散射特性,迭代物理光学法通过不断更新表面电磁流,从而更好地模拟了各个面元间的互耦作用,相对于物理光学方法获得了较高的计算精度。
对于理想导体目标,可得某一个面元上的表面电流如下

当式(6)中的电流达到稳定后,再由式(2)计算可得远区散射场。总之,迭代物理光学方法(IPO)可以将各个面元间的相互作用考虑在内,而弹跳射线方法(SBR)仅可以将射线路径上的面元的相互作用考虑在内,因此,对于结构相对较为复杂的目标,迭代物理光学方法的计算精度会优于弹跳射线方法,但是,所需的计算资源以及计算时间也会有一定程度的增加。因此,本文考虑使用迭代物理光学方法分析海面上的复杂目标,并结合物理光学方法来分析目标与海面的相互作用。
2.3 PO-IPO混合方法原理
对于粗糙面与目标的复合模型,当物体模型相对复杂的时候,则需要考虑粗糙面与目标之间的相互作用。如图1所示,表示入射波的方向,表示粗糙面上由入射波的照射而引发的1阶电流和磁流,表示目标物体上入射波的照射而引发的1阶电流。下标1为电流的阶数,上标s表示粗糙面,t表示目标。图1(a)表示了入射波直接作用于粗糙面和目标所产生的感应电磁流,不考虑粗糙面与目标之间的耦合作用。对于金属目标,1阶感应电流可由计算得到。图1(b)代表粗糙面与目标之间的耦合作用,首先,入射波照射到目标表面产生1阶电流目标表面的1阶电流作为新的源产生了1阶散射电场从而作为新的入射场作用到粗糙面上,在粗糙面上引发了2阶感应电磁流,通过式(3)和式(4)可以计算出粗糙面的2阶感应电磁流。同理,入射波照射到粗糙面上产生1阶电磁流然后产生1阶散射磁场从而可以在物体表面生成2阶感应电流最终,粗糙面上的2阶感应电磁流和物体表面上的2阶感应电流将会在空间产生2阶散射电磁场依次类推,可以得到粗糙面与目标上的各阶感应电磁流,最终可累加得到总感应电磁流
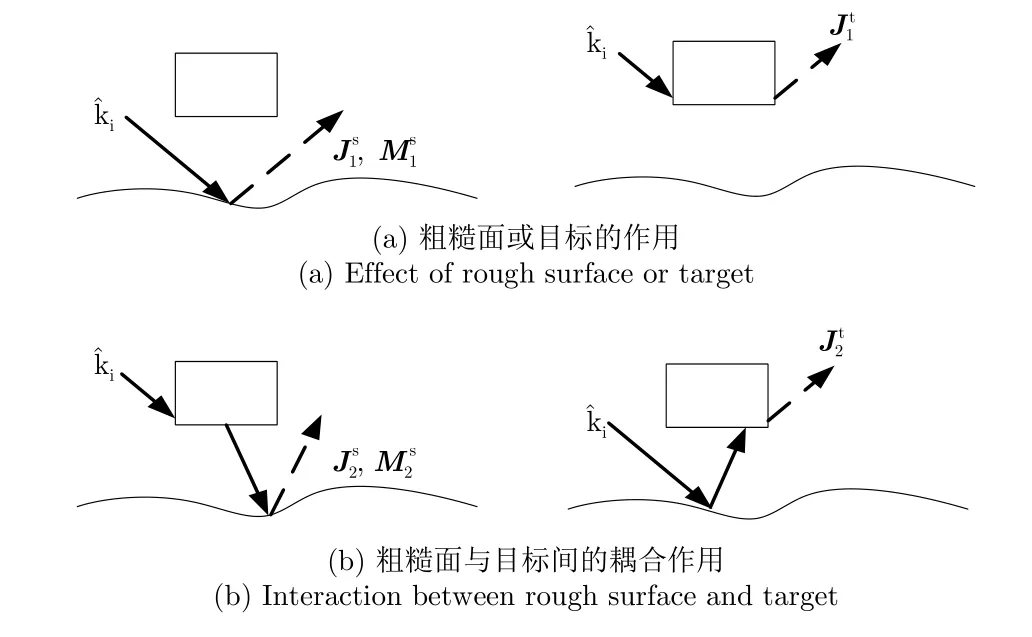
图1 多路径模型基本原理Fig.1 Theory of multipath model
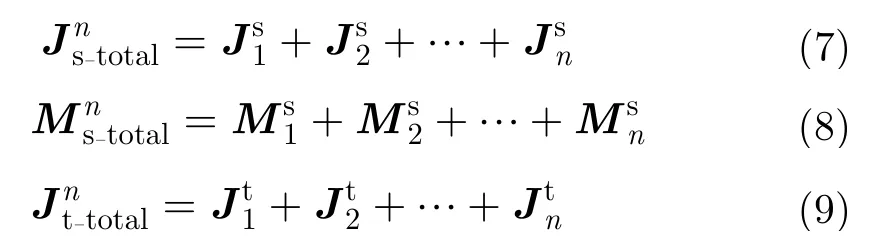
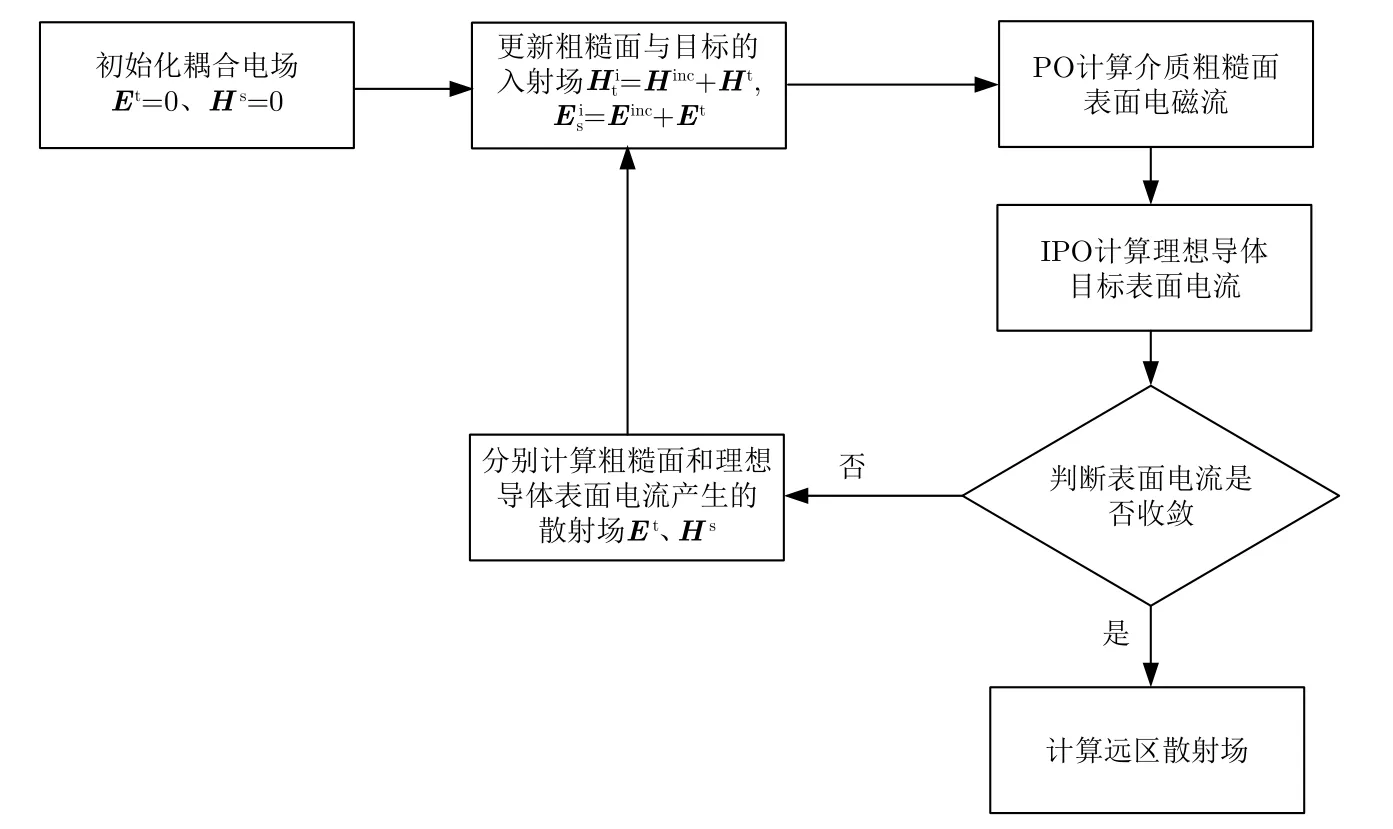
图2 PO-IPO算法流程图Fig.2 Flow chart for PO-IPO
对于分析复杂目标与粗糙面复合模型时,由于物体结构复杂,物体各个面元间的相互耦合作用不可忽略,PO不考虑面元间的相互作用,SBR仅可以将射线路径上面元的相互作用考虑在内,因此使用PO, SBR等方法分析结构较为复杂的目标时会有较大的误差。对于PO-IPO混合方法,粗糙海面上的各个阶的电磁流由PO算法计算得到,假设复杂目标为电大金属目标,则其各个阶的电流由IPO算法得到,粗糙海面与复杂目标之间的耦合作用则使用图1中的处理方式。虽然PO-IPO混合方法的精度相比于PO, SBR的精度要高,但是由于IPO方法需要考虑目标各个面元间的耦合作用,因此POIPO混合方法需要的计算资源相对于PO, SBR要多。如图2给出了PO-IPO算法的流程框图。
3 数值仿真分析
3.1 粗糙海平面的电磁散射计算
假设一个高斯谱生成的3维粗糙面,大小为Lx=Ly=0.6 m ,相对介电常数为=(5.4,j0.04),粗糙面轮廓如图3所示。粗糙面的相关长度为lx=ly=0.06 m ,均方根高度为h=0.1 m。锥形波入射,频率为3 GHz。入射角度分别为θi=30°,60°,= 0°,散射角为- 90°≤ θs≤ 90°,= 0°。分别使用了物理光学方法(PO)、弹跳射线方法(SBR)以及全波数值仿真方法(JMCFIE)对粗糙海面进行了数值仿真,图4是PO, SBR和JMCFIE的入射角度为=30°, VV极化双站RCS的结果对比,图5是PO, SBR和JMCFIE的入射角度为=60°, VV极化双站RCS的结果对比,表1是两种方法消耗资源对比。可以看出,PO能够在保证一定精度的同时,大大节省了计算资源,当浪情较低时,SBR和PO的计算精度基本吻合。因此,PO可作为一种有效的方法来分析粗糙海平面的电磁散射问题。
3.2 舰船的电磁散射计算

图3 PM谱粗糙面模型Fig.3 Model of PM rough surface
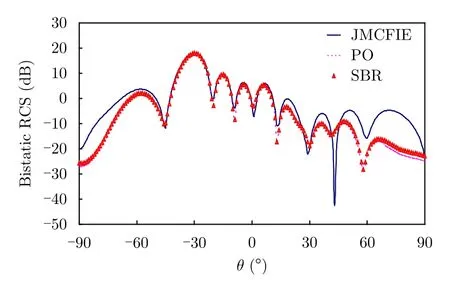
图4 入射角度为=30°粗糙海面模型的双站RCS结果对比
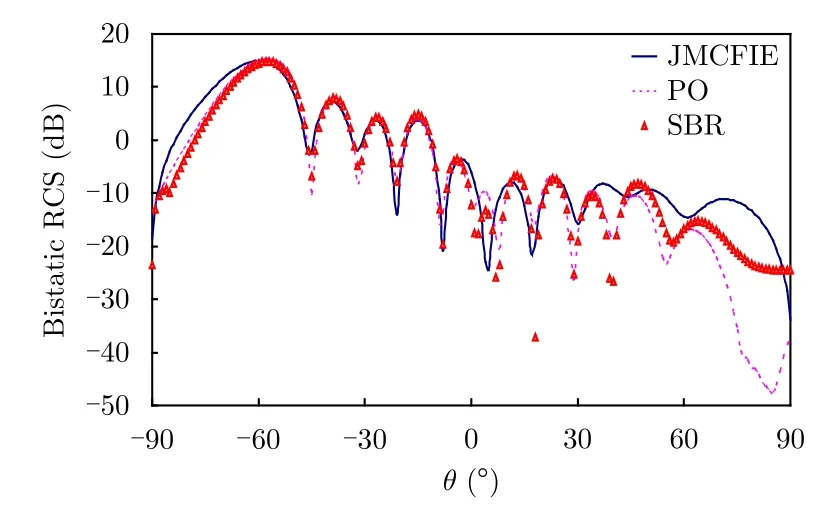
图5 入射角度为 θi=60°粗糙海面模型的双站RCS结果对比

表1 PO与JMCFIE计算资源对比Tab.1 Comparison of computational resources between PO and JMCFIE
考虑一个全尺寸舰船模型的电磁散射特性,如图6所示,舰船长为80 m,宽为12 m,高为14 m。入射波为均匀平面波,频率为500 MHz,入射角为θi=30°,= 180°,极化方式为垂直极化,观察角度为 - 90°≤ θs≤ 90°,= 0°。分别使用了弹跳射线法(SBR)、迭代物理光学方法(IPO)以及全波数值仿真方法(MoM-MLFMA)对舰船进行了数值仿真,如图7所示,给出了3种方法的双站RCS的对比图,表2对3种方法进行了计算资源的对比,可以看出对于这种较为复杂的模型,IPO算法的计算精度比SBR方法要高,但是所需的计算资源要比SBR方法多。因此,分析复杂目标的电磁散射特性时,IPO方法是一个很好的选择。

图6 舰船模型示意图Fig.6 Model of ship
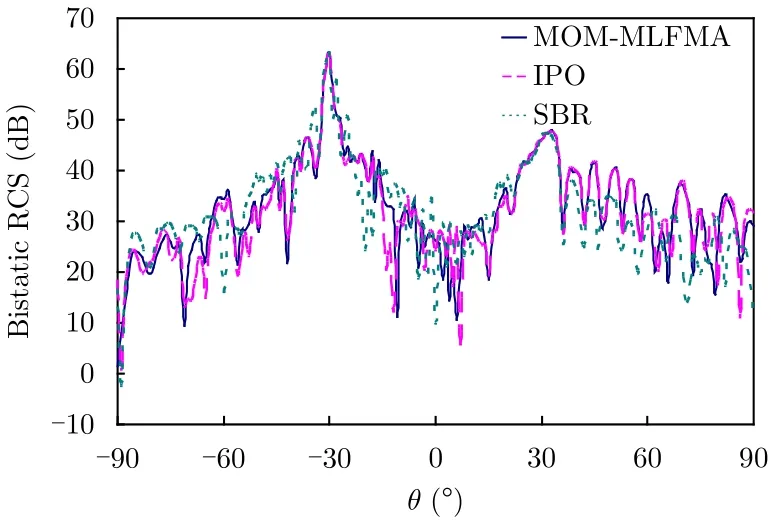
图7 舰船模型的双站RCS结果对比Fig.7 Bistatic RCS results for the ship model
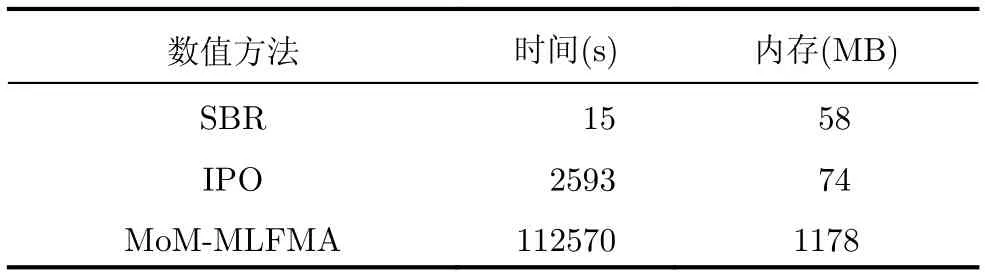
表2 SBR, IPO与MoM-MLFMA计算资源对比Tab.2 Comparison of computational resources among SBR, IPO and MoM-MLFMA
3.3 舰船与粗糙海面的电磁散射计算
首先,仿真了一个舰船与粗糙海面的缩比模型,分别使用了PO-IPO混合方法以及全波数值仿真方法(JMCFIE)对舰船进行了数值仿真,假设一个高斯谱生成的大小为5 1 m×9 m的海面,均方根高度为 0.6 m ,相关长度为 1.2 m,相对介电常数为εr=(5.4,j0.04),上方目标为一长26 m,宽4 m,高4.6 m的理想导体舰船,组合模型示意图如图8所示,入射角为 θi=30°, φi= 180°,入射波频率为0.5 GHz,散射角为- 90°≤ θs≤ 90°, φs= 0°,极化方式为VV极化。如图9所示,给出了两种方法的双站RCS的对比图,表3对两种方法进行了计算资源的对比,可以看出对于这种较为复杂的组合模型,PO-IPO算法的计算精度仍然比较高。
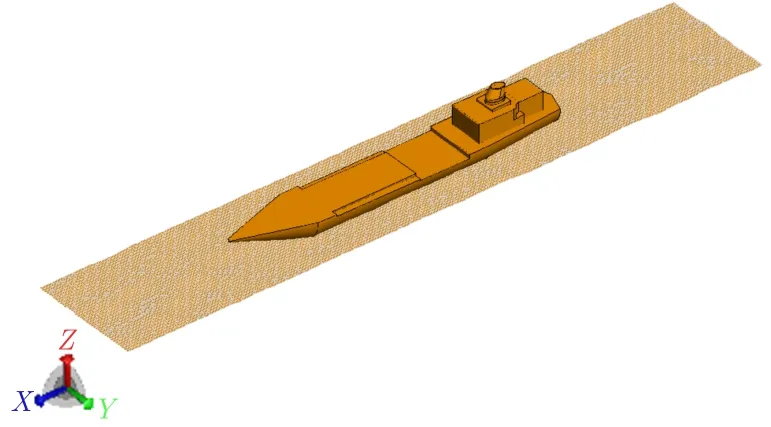
图8 粗糙海面与缩比舰船组合模型示意图Fig.8 Model of ship over rough sea surface
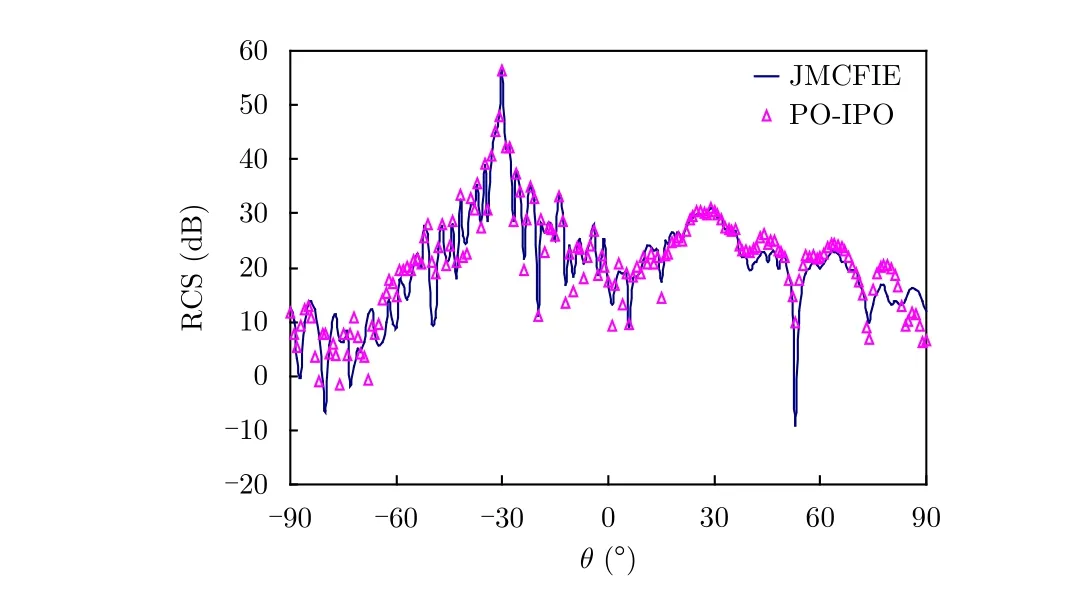
图9 粗糙海面与缩比舰船组合模型的双站RCS结果对比Fig.9 Bistatic RCS results for the ship model over rough sea surface
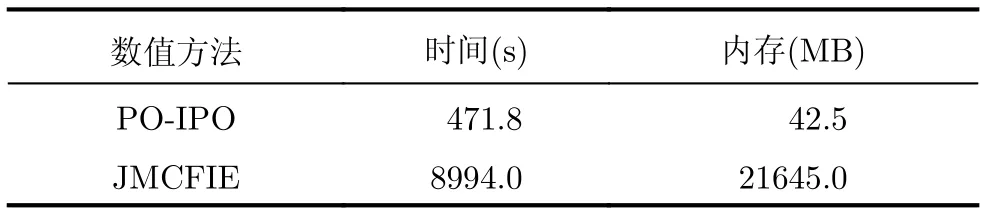
表3 PO-IPO与JMCFIE计算资源对比Tab.3 Comparison of computational resources between PO-IPO and JMCFIE
最后,分析一个全尺寸的带有精细结构的舰船与海面的复合模型,精确的数值仿真方法已经不能够有效地分析这类问题。假设粗糙海面的大小为250 m×40 m,海况设为3级,相对介电常数为εr=(32.3,j30.2),上方有一舰船,舰船长165 m,宽21 m,高59 m,模型如图10所示。入射波为锥形波,频率为30 GHz,入射角为 - 75°≤ θi≤ 75°,φi=0°,垂直极化。由3.1小节和3.2小节的仿真数值结果分析可得,对于舰船模型可使用IPO方法对其进行仿真计算,对于粗糙海面模型可以使用PO对其进行建模计算。如图11所示,使用了PO-IPO混合方法对舰船与粗糙海平面模型进行了单站雷达散射截面积的数值仿真,模型的总未知量个数为320亿,总共使用了100个核进行并行计算,需要内存约为11 GB,每个角度上的计算时间为77 s。
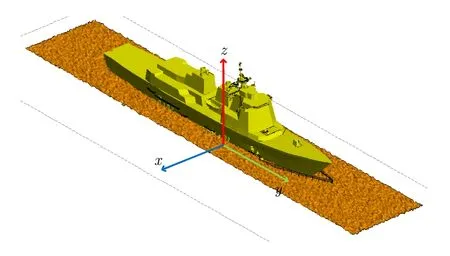
图10 粗糙海面与舰船组合模型示意图Fig.10 Model of full-size ship over rough sea surface
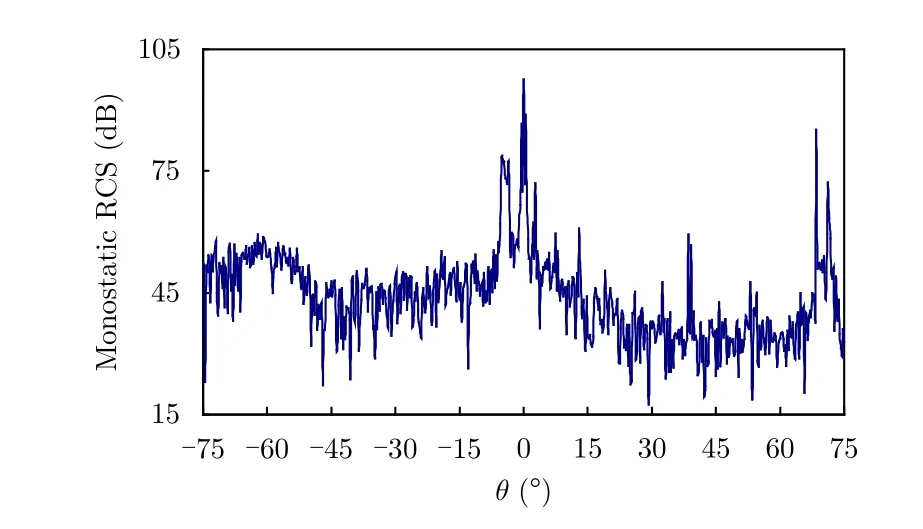
图11 粗糙海面与舰船组合模型的双站RCS结果对比Fig.11 Bistatic RCS results for the full-size ship model over rough sea surface
4 结束语
对于粗糙海面与简单目标的复合模型的电磁散射问题,可以使用PO, SBR等高频方法对其实现高效分析,但是随着目标结构变得复杂,传统高频方法的精度就会受到限制,因此,引入迭代物理光学方法对复杂目标进行计算,从而提出了PO-IPO混合算法。使用PO方法计算粗糙海面的表面电磁流,使用IPO方法计算复杂目标的表面电流,并通过惠更斯原理不断迭代更新两者的表面电磁流,直至达到稳定状态,便可得到远区的散射场。PO-IPO混合方法既考虑了复杂物体本身面元间的互作用,同时考虑了粗糙海面与物体间的耦合,因此可以保证计算效率的同时获得较高的计算精度。

