基于纵向和生存时间结局的联合模型方法及应用*
李淞淋,魏 戌,易丹辉
(1.农业部信息中心 北京 100125;2.中国人民大学应用统计科学研究中心 北京 100872;3.中国中医科学院望京医院 北京 100102)
事物经常是多维度动态发展,这就要求研究者采用全面的、动态的观点来看待问题,即在兼顾多指标协同关系的情况下,进行动态综合评估[1,2]。而当评价指标中既有时间资料,又有纵向指标,就需要构建联合模型进行分析。例如在AIDS研究既关注每立方毫米血浆中CD4细胞的数量,也记录分析患病时间[3,4]。联合模型通过构建纵向评价指标和时间资料的联合分布函数,在考虑指标间关系的基础上,采用极大似然估计方法进行估计,既可以实现对两类评价指标的联合分析,也可以对指标之间相互关系的强度和方向进行衡量[2,5,6]。
值得注意的是,传统的联合模型虽然可以综合分析时间资料和纵向结局指标,但在研究事件发生时间时采用了一个重要却较为苛刻的前提假设——所有的研究单位都必须“死亡”或发生某一被感兴趣的特定事件。也就是说,如果观测时间可以无限延长,则结局事件必然发生,即。但此假设在某些实际研究中并不适用。首先,大多数研究都有一定的时间限制,t→∞的假设并不现实;其次,某些特定事件不是必然的。例如金融危机爆发时,一些企业不会破产或倒闭[7,8]。已有研究发现,当某件事情的发生率低于10%或5%时,)=1这一前提假设将不再合适;同时,从技术层面看,当发生率低于10%或5%时,继续使用传统生存分析方法也无法得到稳健的参数估计结果。
为此,本文在比较分析传统联合模型的适用性与优缺点基础上,探索突破传统联合模型的局限性,尝试对估计方法和统计计算方法进行改进,并应用于缺血性中风早期干预治疗的实际案例。
1 传统联合模型讨论
1.1 适用条件
传统联合分析模型意在考虑指标间潜在关系的基础上,对纵向指标和事件发生时间进行联合分析,尤其适用于如下3种情况:①关注结局事件的发生风险,但希望将纵向评价指标作为协变量引入生存分析模型来解释纵向评价指标对结局事件的影响效果;②关注纵向指标走势,但由于结局事件的发生导致受试患者无法继续被调查,从而致使结局事件发生以后无法继续观测纵向评价指标;③关注纵向评价指标和事件结局发生时间是否有相关关系,则首先假定两个指标相关,搭建两者之间的相关关系,构建联合模型,然后再在对相关关系进行检验,最终确定这两类结局指标之间的关系有无与大小。
1.2 传统联合模型形式
传统联合模型(Joint Model)由两部分构成:纵向数据部分和时间资料。假设对m个个体在时间段[0,τ)上进行观测。第i个个体提供了一系列(可能有部分缺失)的纵向测量指标{yij,j=1…ni},对应的观测时间为{sij,j=1,…,ni},此外还有某一特定结局事件发生前的“生存时间”ti(或许会存在删失的情况)。定义Ti为观测到的第i(i=1,…,m)个个体的失效时间(Failure Time),等于真实事件的发生时间(True Event Time)T*i和删失时间(Censoring Time)Ci中偏小的那一个,即Ti=min(T*i,Ci)。另外,定义事件发生的标识为 δi=I(Ti*≤ Ci),其中 I(⋅)是指示函数,当 Ti*≤ Ci时函数取值为1,否则取值为0。于是可将观测到的事件时间的数据写成集合{(Ti,δi),i=1,…,m}的形式。传统联合模型(Joint Models)的一般形式为:
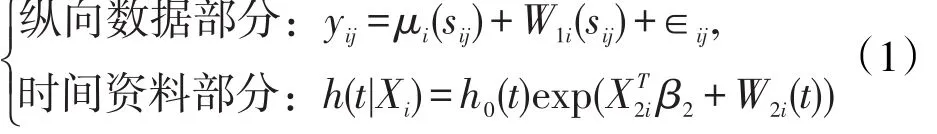
其中,X2i为解释变量,β2为与其对应的回归系数;W2i(t)的形式类似于纵向数据模型中的W1i(sij),包括个体随机效应部分和脆弱项(Frailty)。于是联合分析主要体现在:一是具有一些相同的解释变量;二是W1i(sij)和W2i(t)是度量同一受试个体的随机效应。
1.3 传统联合模型的优势和不足
传统联合模型利用随机效应和脆弱项来衡量个体差异并解释两个评价指标之间的相关关系,基于Wulfsohn和Tsiatis在1997年提出的经典假设——“给定随机效应的情况下,纵向指标与时间资料条件独立”,构建两个结局指标的联合分布函数,然后计算似然函数并求解参数估计值。但是,传统联合模型要求随机效应必须服从正态分布,且事件发生率随着时间延长而趋向于1。这些假设条件极大地限制了模型的适用环境。
2 带混合Cure的扩展联合模型
2.1 模型扩展的依据和思路
带混合Cure的扩展联合模型是在传统联合模型基础上,放宽假设条件,允许随机效应服从指数族分布即可,且不要求结局事件必须发生,从而使模型在小概率事件的环境中也可以得到科学的结果。模型扩展的依据,一是传统联合模型,二是混合Cure模型。
混合Cure模型最早起源于医学研究领域。Ziegel等[9]研究指出,随着技术手段的提高和医疗条件的改善,长期存活个体(Long-Term Survivor)即被治愈的病人数量偏多,死亡等结局事件发生率较小,成为小概率事件。为了分析这些小概率发生的事件,多位学者[10-15]提出了混合Cure模型。
混合Cure模型假设总人群(Whole Population)可以分为g个亚组,i=1,2,…,g,Zi,Xi是第i个个体的两个协变量向量,Zi中除了有元素1外,还享有Xi中的部分元素。每个亚组在全人群中所占比重为πi(Zi),每个亚组内人群的“死亡”模式相同,即密度函数为fi(t |Xi),累积函数为Fi(t |Xi)。
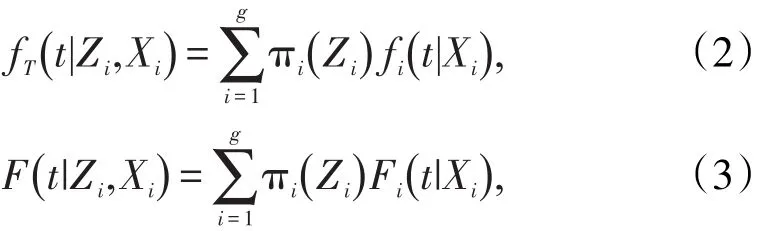
在混合治愈模型中,最常见的情况是总人群可以分为两个亚组:一组是根本不可能发生结局事件的免疫(或治愈)人群组;另一组则是将研究时间无限延长的话,必将发生结局事件的人群。值得注意的是,由于研究时间有限,不可能无限期延长,因此后一组人群虽然具有发生结局事件的可能性,但在有限的研究时期内,我们只能观察到其中部分人群实际发生了结局事件。假定,在流行病调查研究中,由于个体抵抗力不同,有一些人是不会感染某种疾病的,即“非易感人群”或“治愈人群”,π1(Zi)=1-p(Zi);另一类则是“易感人群”或“未治愈人群”,π2(Zi)=p(Zi)。于是,全体人群的分布函数FT(t |Zi,Xi)和生存函数ST(t |Zi,Xi)可分别写成公式(3-3)和公式(3-4)。
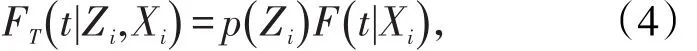
和
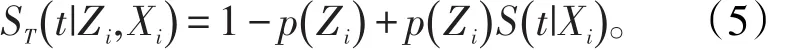
其中,F(t|Xi)和S(t|Xi)分别是“未治愈人群”的分布函数和生存函数,
2.2 扩展联合模型的形式和前提假设
2.2.1 扩展联合模型的一般形式
假设总人群(Whole Population)中有N个个体,i=1,2,…,N,分为g个亚组,j=1,2,…,g,但这g个亚组不是预先被分好的,而是在诊疗或干预的过程中自然形成的。引入标识变量rij,若研究结束后第i个个体进入了第 j组,则有rij=1,否则rij=0。记第 j个亚组包含了Nj个个体,则
研究过程中,对这N个个体在时间段[0 ,τ)上进行观测,个体i被观测两套协变量向量Xi={Xi和 Zi分别包含了q1和q2个协变量。对第i个个体在观测时间序列上进行ni次观测得到一组(可能有部分缺失)纵向测量指标得分,构成纵向结局指标的取值向量Yik={yi1,yi2,…,yik;k=1,2,…,ni};此外,研究还记录了个体i发生某一感兴趣结局事件的时间Ti(或许会存在删失的情况)。研究假定,个体i发生此结局事件后就将离开此研究,不再进行后续的测量。
定义Ti为观测到的第i个个体的特定事件的发生时间,它等于事件的真实发生时间(True Event Time)和删失时间(Censoring Time)C中偏小的那个,即iTi=min()。另外,定义事件发生的标识为 δi=I(Ti*≤ Ci),其中 I(∙)表示指示函数,当Ti*≤Ci时,δi=1,表示即研究期间内观察到个体i发生了结局事件,否则δi=0。于是结局事件的发生情况可写成集合{(Ti,δi);i=1,…,N},而所有结局指标的取值效率可以表示成集合{(Yi,Ti,δi,rij);i=1,…,N;j=1,…,g}。
考虑到经过良好的、有效的措施的干预,研究总体的治愈率或免疫力会提高,因此,不良结局事件的发生率很低,limt→∞F(t)=1的假设将不再适用,需要为每个个体落入第 j个亚组的概率 pj=E(Nj/N)进行估计,
于是,“带混合Cure的扩展联合模型”由纵向数据子模型、人群分类子模型和时间资料子模型等三部分构成,一般形式如公式(2)。
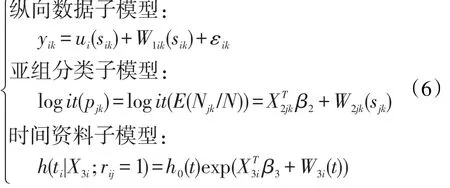
纵向数据子模型是对研究期间内的纵向评价指标走势进行拟合分析,其中ui(sik)为固定效应部分,W1ik(sik)为随机效应部分,εik为测量误差。若纵向数据子模型为线性混合效应模型,有,即此子模型为。纵向数据子模型暂时假定给定其他结局评价指标,纵向评价指标的条件分布为正态分布,将来还可以扩展到指数分布族。
亚组分类子模型和时间资料子模型类似于混合Cure模型,但都被进行了一定程度扩展。亚组分类子模型为多分类的广义线性混合效应模型,引入了随机效应,从而允许各亚组比例在整个研究过程中发生变化,实现对事件发生率或疾病治愈率的动态分析。
时间资料子模型是对第i个个体在研究时期内每个时间点上的结局事件发生风险进行分析,第i个个体属于第 j组的概率为 pjk。该子模型引进了脆弱项W3i(t)=f2(b),允许个体差异的存在,同时脆弱项的存在将纵向结局指标yi和事件发生风险h(ti|X3i;rij=1)联系起来。例如表示:对于第 j组内的每个个体而言,个体效应b0每增加一个单位,其发生该研究事件的风险提高约倍。
需要指出的是,X1ik、X2jk和X3i是解释变量X的子集,它们可以不相等,可以有相同的部分;Z1ik是解释变量向量Z的子集;β1、β2、β3、b分别为 X1ik、X2jk、X3i和 Z1ik的待估系数,参数向量 γ1=(γ10,γ11,…,γ1m)和 γ2=(γ20,γ21,...,γ2m)则分别是脆弱效应 W2jk(sjk)和W3i(t)中b的待估系数向量。这是与此前关于联合分析纵向-生存-治愈模型的研究[16]不同的地方,因此需要使用修正的半参数极大似然估计方法进行估计,使用广义半参数似然比检验进行评估。
2.2.2 联系纵向评价指标与结局事件发生概率和发生时间的方法
扩展模型搭建纵向评价指标、结局事件发生率和发生时间的联系如下:①三个子模型有相同的协变量和参数,构建固定效应部分的关系;②纵向数据子模型的随机效应系数b是亚组分类子模型和时间资料子模型中脆弱项的协变量,将个体效应与结局事件发生率和发生时间联系起来;③参数向量 γ1=(γ10,γ11,…,γ1m)和 γ2=(γ20,γ21,…,γ2m)的大小可以衡量纵向评价指标与结局事件发生率和发生时间的关系强度的大小和方向。
2.2.3 联合模型的前提假设
扩展模型需要满足一定的前提条件:①纵向评价指标和结局事件发生率及发生时间是对同一群体在同一个研究中进行的测量;②三个结局指标(纵向结局指标、结局事件发生率、事件发生时间)之间可能存在一定的关系;③在给定随机效应或个体差异的情况下,纵向结局指标和结局事件发生率及发生时间是条件独立的。
3 应用分析
3.1 问题说明
本研究依托于一项“863”课题,目的是综合评价中医综合治疗方案和西医治疗方案针对缺血性中风早期干预治疗效果。该课题得到的多家医疗单位的支持,采用中央随机的方法对来自多家医疗中心的1 052例缺血性中风早期病患进行随机对照试验,随机进入中医组和西医组的比例是2∶1。
根据有关医学知识,确定了评价治疗中风的药物一年内的疗效指标有NIHSS量表得分和死亡风险及发生时间。美国国立卫生研究院卒中量表(National Institute of Health Stoke Scale,NIHSS)是Thmos等为了急性脑卒中的治疗研究于1989年设计的一个包含了15个项目的神经功能检查量表。截至目前,该量表包含了每个脑动脉病变可能出现的神经系统检查项目、精神状态检查项目、感觉机能、瞳孔反应和足底反射项目等。量表得分越高说明疾病状态越严重。此量表使用简便、重测信度高、内容一致性好,现已被广泛用于脑卒中研究的定期测量记录。此外,脑卒中研究还特别关注死亡这一客观的结局指标,如果死亡率或死亡风险高,则意味着治疗方案的效果非常差。然而,值得特别注意的是:截至目前,已经有很多关于脑卒中治疗的研究发现,NIHSS量表得分与死亡风险并不是孤立存在的,两个结局评价指标之间可能存在一定联系。有关研究[1,17,18]发现:伴随着NIHSS评分值的增高,死亡风险性明显增加。
由上所述可知,目前尚无确凿证据证明“NIHSS评分”与“因脑卒中致死”存在必然的因果关系,但是二者之间确实存在明显的、不可被忽视的关系。同时,由于本研究只收集到1年的数据,患者的病死率较低(低于10%),为了得到更加准确的估计结果,决定采用带混合Cure的联合分析扩展模型进行研究。
3.2 数据说明
3.2.1 变量介绍
该研究分为住院治疗期和出院预后观察期两部分。第一部分时长为21天,分别在0天(入院的当前或前一天)、7天、14天和21天时使用NIHSS量表进行测量,即NIHSS得分为本研究中的纵向评价指标。此外,对1 052个患者1年内的生存状况进行跟踪调查,及时、准确的记录每个患者的生存状况、死亡情况及死亡事件。下面将本研究所关注的一些变量名称及其符号进行说明:“r_group”表示随机分组(r_group=0表示西医组,r_group=1表示中医组);“obstime”表示NIHSS量表的测量时间;“r_group*obstime”表示治疗组与治疗时间的交互效应,也就是考察每一个随机分组的NIHSS量表得分随观测时间的变化趋势。评价指标中,“Y”为 NIHSS量表得分,“t_death”为生存时间,“death”表示在研究过程中受试者是否死亡(death=1表示死亡,death=0表示删失,即在1年内尚未观测到患者死亡)。因为在建模前先对个别指标的极少量缺失值进行处理。于是,在后续研究中,所用数据中不存在数据缺失的情况。
3.2.2 基期比较
除了研究关注的结局指标外,此随机对照试验对入组人群的基本情况和可能影响疗效评价结果的混杂因素,例如年龄、性别、病程、主要合并病和主要并发症等都进行了随机。经过对这些指标的统计学检验(表1-5),发现这些指标在两组中的分布没有显著差异,即试验的随机效果很好。
表1 两组间年龄比较(

表1 两组间年龄比较(
n P值组别中西医结合组西医组年龄(岁)62.88±10.13 63.18±10.48 T值701 351 0.44 0.66

表2 两组间性别比较
表3 两组间病程比较

表3 两组间病程比较
n T值P值组别中西医结合组西医组701 351病程(小时)49.48±54.62 52.77±59.65 0.892 0.373

表4 两组间主要合并病比较

表5 两组间主要并发病比较
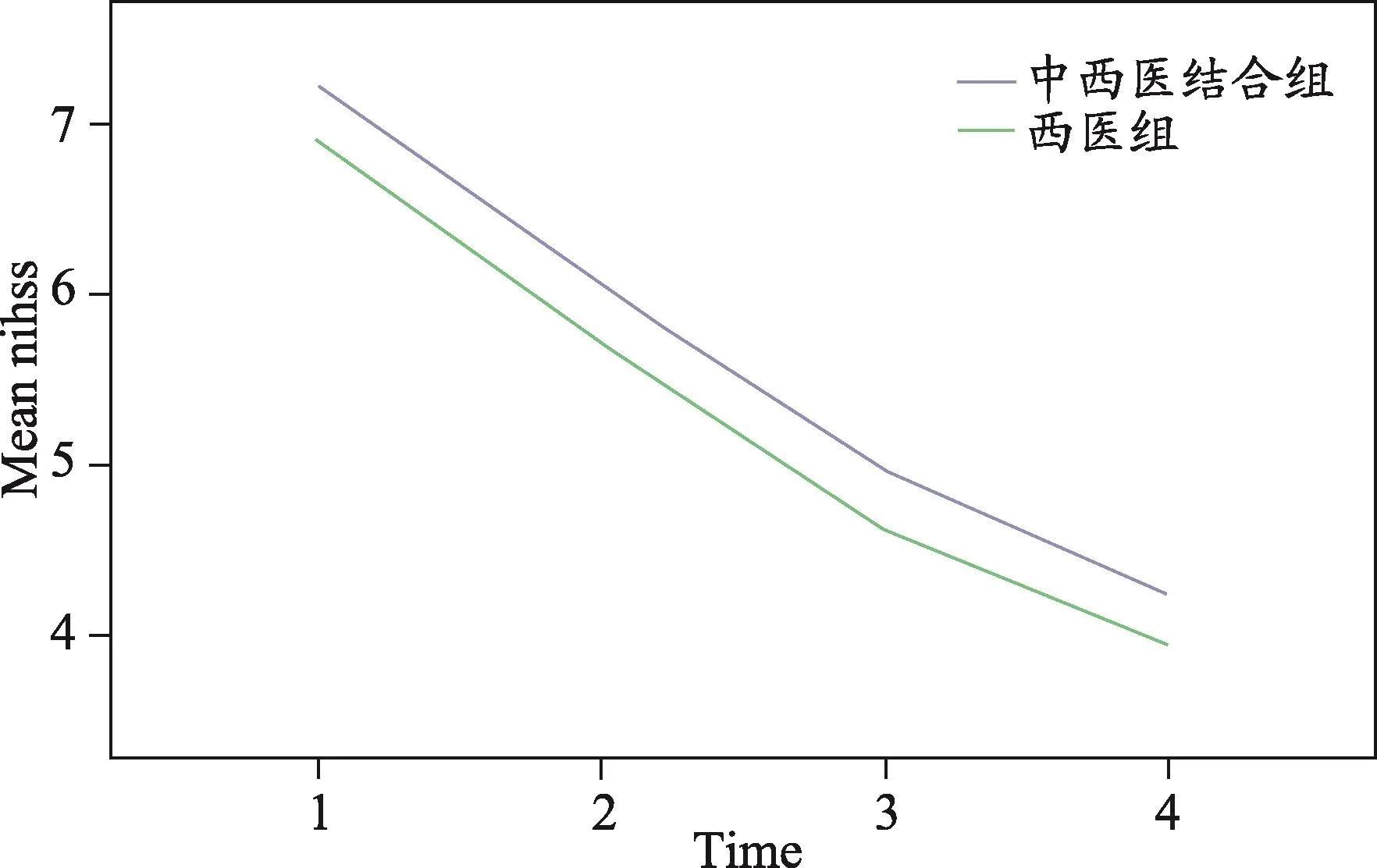
图1 两组的NIHSS量表得分在4个时间点上变化趋势图
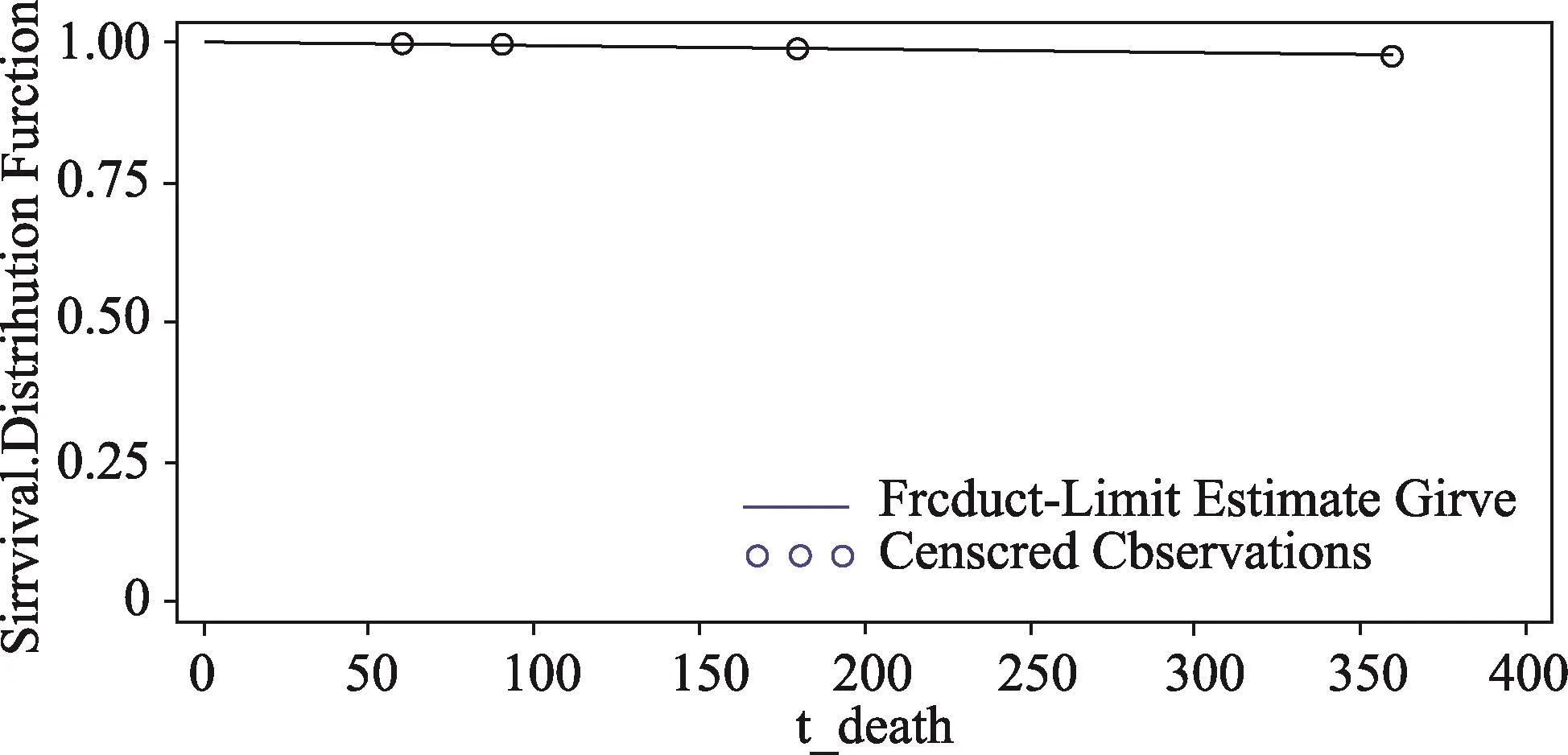
图2 研究人群1年内的生存函数图
绘制并分析两组的NIHSS量表得分在0、7、14、21天这4个时间点上的发展曲线(图1)以及研究人群在1年中的生存函数曲线(图2)。由图1可见,两组的NIHSS量表得分存在差异;由图2可以看出,1年内因脑卒中致死的人数不足总人群的10%。因此,需要采用本研究提出的带混合Cure的联合分析扩展模型进行分析。
3.2.3 模型构建
第一步,讨论评价指标的分布特征,确定扩展联合模型中每个子模型的形式。因为没有充分的证据可以拒绝“给定随机效应的情况下,纵向评价指标条件地服从正态分布”这一原假设,为此纵向数据子模型继续采用线性混合效应模型;从死亡率不高于10%来看,这些患者经过治疗,应该是出现了“治愈”和“延长生存时间”两种结局事件,这也与已有研究的结论[1,17,18]一致。但为了进一步确定事件发生时间子模型的形式,使用图示法数值法拟合和拟合优度评价的方法进行分析,最终确定生存时间服从Weibull分布。
第二步,变量选择。本文使用后退法进行变量选择,标准为参数的t检验、半参数似然比检验和模型整体拟合效果的半参数似然函数值.
第三步,构建模型。根据以上分析,确定模型形式为公式(7)。
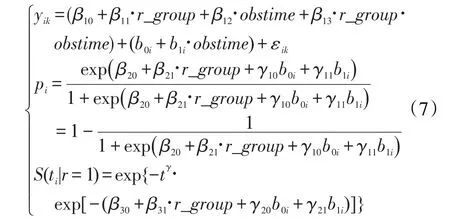
其中,每个变量和参数的含义见公式(6)的相关介绍。对于个体i而言,治愈率为1-pi,未治愈的话则具有生存函数S(ti|r=1)。
死亡概率为
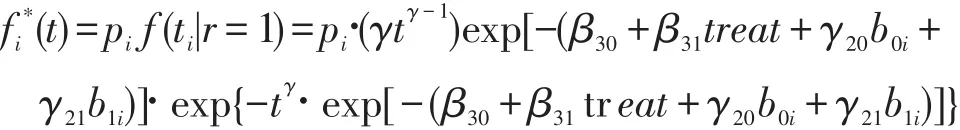
个体i对似然函数的贡献为{Yi,Ti,δi,bi}的对数联合似然函数为 Li(θ)。
Li(θ)=LLi(θ)+LSi(θ)+LMi(θ)。其中,
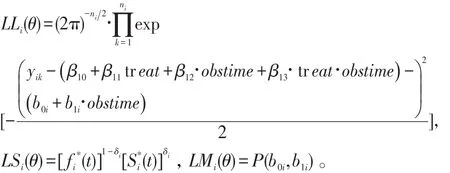
3.2.4 模型估计和检验
基于SAS9.2的NLMIXED模块,使用半参数极大似然估计方法进行模型估计(表6)。
构 建 半 参 数 似 然 比 统 计 量 为 lrtn(β13,β21,β31)=17 422-9 933.67=7 488.33,根据自由度为3的卡方分布 χ2(3),计算P值为<0.000 1。显著拒绝原假设 β13=0,β21=0,β31=0,即中医组疗效显著优于西医组。
3.2.5 模型结果分析
从表6所得每个待估参数的半参数估计结果,可知:
(1)在纵向分析子模型中,β10=7.229 2说明入组时(0天)西医组的NIHSS平均值是7.229 2,显著非0;β11=-0.382 2说明中医组中患者在入组时的NIHSS得分均值为7.229 2-0.382 2=6.847 0,但检验得两组人群入组时的NIHSS得分无显著差异;β11=-0.143 2说明在21天的治疗过程中,西医组NIHSS日均下降约0.143 2,显著非0;β13=-0.000 3说明在21天的治疗过程中,中医组NIHSS日均下降0.143 2+0.000 3=0.143 5,但检验结果显示与西医组无显著的统计学差异。
(2)基于亚组分类子模型,计算未被完全治愈的患者所占比例为
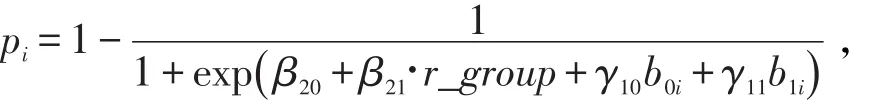
治愈率为
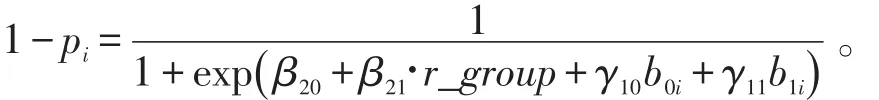
β20=8.058 1说明西医组的平均治愈率为说明中医组的平均治愈率为,经检验显著优于西医组,约为其exp(3.168 6)≈23.77倍;γ10=1.492 0>0且显著非零,说明入组时NIHSS得分越高、病情越重的患者,被治愈的可能性越小,0天时NIHSS得分每提高1分,治愈率降低0.775 1;γ10=2.503 4>0且显著非零,说明治疗过程中NIHSS分数下降越明显,即对治疗方案有明显反应的患者,被治愈的可能性越高,治疗过程中NIHSS日均降幅每增加1,治愈率提高exp(2.503 4)≈11.224 0倍,若NIHSS日均降幅每增加0.1,治愈率提高约exp(0.250 3)≈ 28.45%。
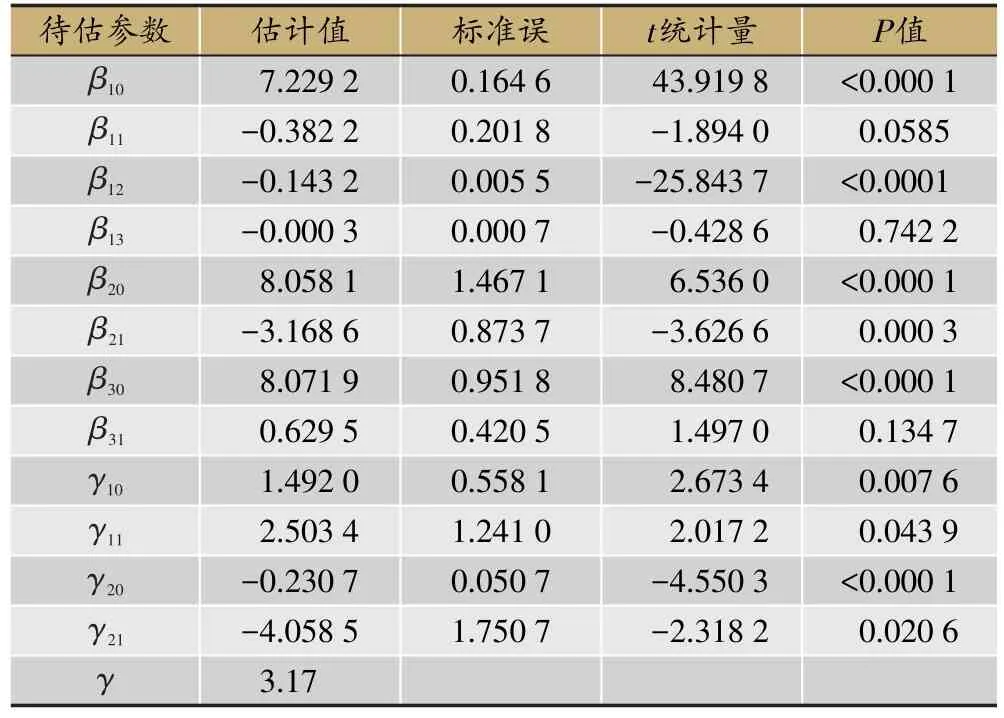
表6 扩展后联合模型的半参数极大似然估计结果汇总表
(3)时间资料子模型中,β30=8.021 9意味着西医组平均生存函数为exp{-tγ·exp(-8.021 9)};β31=0.629 5不显著非零,即中医组平均生存函数exp{-tγ·exp(-8.651 4)},与西医组无显著差异;γ20=-0.230 7<0说明患者基线的NIHSS得分越高,即入组时脑卒中病情越重,患者的生存函数越小;同理可以发现,治疗过程中患者NIHSS降低速度越慢,生存函数越小。
(4)从半参数似然比检验结果看,统计量lrtn(β13,β21,β31)≈7 488.3,结合(2)、(3)可知中医组疗效显著优于西医组,主要体现在前者对高病人治愈率和延长生存时间方面显著优于西医组。
4 讨论与结论
4.1 扩展后的联合模型更适用于临床治疗的综合评价
从理论角度,传统联合模型联合分析纵向和生存时间结局,并研究两类结局指标之间的关系;扩展的联合模型吸收传统联合分析方法和混合Cure模型的优点,不再继续假设随机效应和脆弱项服从正态分布,仅要求随机效应的期望为零,并使用半参数估计方法和合适的算法,有效扩大适用范围。从推广应用角度看,扩展后联合模型更适用于临床治疗方案的综合评价,具体体现在:①放宽了临床疗效评价的数据类型:目前一些多靶点的临床试验具有多维度、多数据类型的评价指标,扩展后联合模型不假定数据分布,非常适用于此类型试验的分析;②提供了医学伦理要求下,科学评价急、重症治疗方案的模型技术:传统医学统计模型需要依托大样本数据,受医学伦理要求,无法应用于癌症、中风等急、重症疾病临床治疗的效果评价中,而创新后模型打破了样本数据量的限制,提高了分析精度,增强了临床推广应用性;③可综合分析临床疗效和安全性,获得准确的试验预期:当前不少临床试验以AD事件发生率作为安全性指标,扩展后的联合模型可分析提高疗效所需承担的风险,还可探索治疗方案的副作用。
4.2 入组NIHSS得分与治愈率、治愈时间有显著关系。
用扩展的联合模型分析缺血性中风早期干预的疗效,有效地实现了死亡率极低地情况下,对NIHSS量表得分与结局事件发生率和发生时间的联合分析,研究发现:①入组时NIHSS得分越高、病情越重的患者,被治愈的可能性越低;治疗过程中NIHSS分数降速越快,即对治疗方案有明显反应的患者,被治愈的可能性越高;中西医结合治疗方案的治愈率约为是西医组的exp(3.168 6)≈23.77倍;②患者入组时NIHSS得分越高,即入组时脑卒中病情越重,患者的生存函数越小,即治愈率越低,治愈所需时间越长;治疗过程中患者的NIHSS降低地越慢,生存函数越小。

