椭圆曲线y2=x3+23x+54的正整数点

杜先存, 过 静

(1. 红河学院 教师教育学院, 云南 蒙自 661199;2. 江西科技师范大学 数学与计算机科学学院, 江西 南昌 330013)

三次丢番图方程是一类基本的丢番图方程,目前研究比较多,例如文献[1].椭圆曲线是一类特殊的丢番图方程,其整数点是数论中基本而又重要的问题,关于椭圆曲线y2=nx(x2+a2)的整数点,目前已有一些结论,如文献[2].关于椭圆曲线

y2=x3+(q-4)x-2q

(1)

的整数点问题,目前主要集中在q=31上,此时椭圆曲线(1)成为椭圆曲线

y2=x3+27x-62.

(2)

1987年,D.Zagier[3]提出了椭圆曲线(2)的整数点的问题,该问题对于讨论椭圆曲线的算术性质有重要的意义;2009年,Zhu等[4]运用代数数论和p-adic分析方法找出了椭圆曲线(2)的全部整数点;2010年,吴华明[5]运用初等数论方法给出了椭圆曲线(2)的全部整数点;同年,贺艳峰[6]同样运用初等数论方法给出了椭圆曲线(2)的全部整数点.在此基础上,2014年,管训贵[7]给出了椭圆曲线(2)的更一般的推广.而关于椭圆曲线

y2=x3+(q-4)x+2q

(3)

的整数点问题,目前主要集中在q=31上,此时椭圆曲线(3)成为

y2=x3+27x+62.

(4)

2016年,过静[8]运用初等数论方法给出了椭圆曲线(2)的全部整数点;在此基础上,2017年,杜先存[9]给出了椭圆曲线(4)的更一般的推广.本文仅研究的是q=27时椭圆曲线(3)的正整数点的情况,即给出了以下定理:

定理椭圆曲线

y2=x3+23x+54

(5)

无正整数点.

1 相关引理

引理1[10]若D是一个非平方的正整数,则方程x2-Dy4=1至多有两组正整数解(x,y),而且方程恰有2组正整数解的充要条件是D=1 785或D=28 560或2x0和y0都是平方数,这里(x0,y0)是方程x2-Dy2=1的基本解.

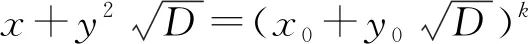
2 定理证明

证明 设(x,y),x,y∈Z+是椭圆曲线(5)的正整数点,由(5)可得:

y2=(x+2)(x2-2x+27).

(6)

因为gcd(x+2,x2-2x+27)=gcd(x+2,35)=1或5或7或35,所以分别讨论这4种情形下椭圆曲线(6)的正整数点的情况.

情形Ⅰx+2=u2,x2-2x+27=v2,y=uv,gcd(u,v)=1,u,v∈Z+

因为u2≡0,1(mod 4),所以x=u2-2≡2,3(mod 4),则x2-2x+27≡2,3(mod 4),而v2≡0,1(mod 4),故有2,3(mod 4)≡x2-2x+27=v2≡0,1(mod 4),显然矛盾,故该情形下椭圆曲线(5)无正整数点.

情形Ⅱx+2=5u2,x2-2x+27=5v2,y=5uv,gcd(u,v)=1,u,v∈Z+

因为u2≡0,1,4(mod 8),所以x=5u2-2≡2,3,6(mod 8),故x2-2x+27≡3,6(mod 8),而v2≡0,1,4(mod 8),则5v2≡0,4,5(mod 8),故有3,6(mod 8)≡x2-2x+27=5v2≡0,4,5(mod 8),显然矛盾,故该情形下椭圆曲线(5)无正整数点.

情形Ⅲx+2=7u2,x2-2x+27=7v2,y=7uv,gcd(u,v)=1,u,v∈Z+

因为u2≡0,1,4(mod 8),所以x=7u2-2≡2,5,6(mod 8),则x2-2x+27≡2,3(mod 8),而v2≡0,1,4(mod 8),则7v2≡0,4,7(mod 8),故有2,3(mod 8)≡x2-2x+27=7v2≡0,4,7(mod 8),矛盾,故该情形下椭圆曲线(5)无正整数点.

情形Ⅳx+2=35u2,x2-2x+27=35v2,y=35uv,gcd(u,v)=1,u,v∈Z+

(12e2-1)2+416e4=v2.

(7)

即

(v+12e2-1)(v-12e2+1)=416e4.

(8)

因为2|u,故由x+2=35u2知2|x,则由x2-2x+27=35v2得2v,故2|(v-12e2+1),所以gcd(v+12e2-1,v-12e2+1)=gcd(24e2-2,v-12e2+1)=gcd(2(12e2-1),v-12e2+1)=2gcd(12e2-1,v-12e2+1)=2gcd(12e2-1,v).

由式(7)得gcd(12e2-1,v)=gcd(12e2-1,416e4)=gcd(12e2-1,416)=1或13,故gcd(v+12e2-1,v-12e2+1)=2或26,因此式(8)可分解为

(9)

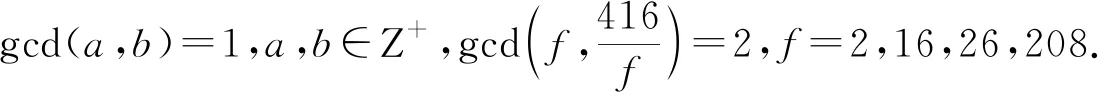
由式(9)得:

(10)

情形ⅰ 若gcd(v+12e2-1,v-12e2+1)=2.对式(10)两边取模4,得:

(11)

当f=2,26时,式(11)为

(12)

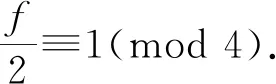
当f=16时,式(10)为12a2b2-1=8a4-13b4,则有24a2b2-2=16a4-26b4,配方得35b4-(4a2-3b2)2=2,两边取模5得:

(4a2-3b2)2≡-2(mod 5).

(13)

当f=208时,式(10)为12a2b2-1=104a4-b4,配方得:

(b2+6a2)2-140a4=1.

(14)

令p=b2+6a2,p∈Z+,则式(14)为

p2-140a4=1.

(15)

令w=2a2,w∈Z+,则式(15)为

p2-35w2=1.

(16)

因为Pell方程(16)的基本解为(p1,w1)=(6,1),则方程(16)的全部正整数解可表为

由此可知方程(15)的正整数解满足:

(17)

即

(18)

因为Pell方程p2-140a2=1的基本解为(p1,a1)=(71,6),则2p1=142,故2p1,a1均不为平方数,又D=140≠1 785且D≠28 560,故由引理1知方程(15)至多有一组正整数解.

由引理2知方程(15)若有一组正整数解,则n=2或2n,因此n=2.

若n=2,由式(17)知2a2=12,即a2=6,显然无解,故n=2时,式(17)不成立,因此f=208时情形ⅰ不成立.

综上,情形ⅰ不成立.

情形ⅱ 若gcd(v+12e2-1,v-12e2+1)=26.对式(10)两边取模13,得:

(19)

情形(ⅰ) 当f=2,16时,因为gcd(v+12e2-1,v-12e2+1)=26,则由v+12e2-1=fa4知13|a,则式(19)成为-1≡0(mod 13),显然矛盾,故情形(ⅰ)不成立.

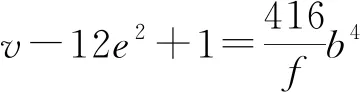
综上,情形ⅱ不成立.

综上所述定理得证.