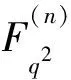酉空间上一类析取矩阵的构造及紧界分析
张丽华, 牛美芳
(沈阳师范大学 数学与系统科学学院, 沈阳 110034)
0 引 言

1 酉空间中的计数定理回顾
设q是一个素数的方幂,Fq2是一个含有q2个元素的有限域,Fq2有一个2阶自同构
∀a∈Fa2


而

是Fq2上的n维向量空间。
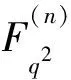


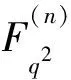
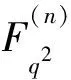
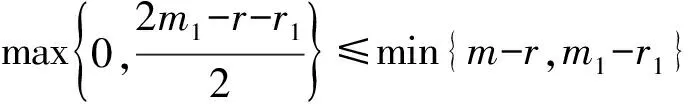
2 dz析取矩阵的构造
2.1 dz析取矩阵的定义

下面讨论d和z的取值范围,并给出z的紧界。
2.2 z的紧界分析
与文献[10]类似,令Hi=Di∩D0(i=1,2,…,d),那么

比较式(2)和式(3)可得
N(r,s-1;m-1,s-1;n)>N(r,s-1;m-1,s;n)
所以下面只需考虑Hi为(m-1,s-1)型子空间的情形。
假设Hi是包含在(m,s)型子空间D0中的某个(m-1,s-1)型子空间,由式(1)知Hi的个数为
≜b

(4)

由式(1)知
N(r,s-1;m,s;n)=bN(r,s-1;m-1,s-1;n)
于是当2≤d z=N(r,s-1;m,s;n)-dN(r,s-1;m-1,s-1;n)=(b-d)N(r,s-1;m-1,s-1;n)>0 因此当2≤d 当d≥b时 所以当d≥b时Mq2(r,s-1;m,s;n)不是dz析取矩阵。3 结 语