近似熵与样本熵在静息态fMRI数据中的对比研究

陈 慧， 孟攀婷， 朱登辉， 赵 晨， 张亮亮

(1.郑州轻工业大学 工程训练中心， 河南 郑州 450000; 2.郑州轻工业大学 计算机与通信工程学院， 河南 郑州 450000)

0 引言

随着功能磁共振成像(functional magnetic resonance imaging,fMRI)的迅速发展，越来越多的人开始进行fMRI的研究.大脑是一个非常复杂的非线性系统，近几年来越来越多的非线性方法被广泛应用于fMRI中以探索大脑功能的非线性特征信息，其中用之较多的是通过熵[1-4]从时间序列的复杂性角度来探索大脑的功能活动.

Sokunbi等[5-7]的研究表明将近似熵(approximate entropy,ApEn)方法应用于fMRI中是可行的、有效的.Sokunbi等随后的一系列研究尝试将样本熵(sample entropy,SampEn)方法应用于fMRI中，结果发现SampEn方法在区分正常人与疾病(注意力不集中症、精神分裂症)患者、年轻人与老年人方面均具有较好的效果.以上研究表明ApEn方法与SampEn方法在fMRI研究中均具有较好的应用前景，然而究竟采用哪种算法分析fMRI数据更有效，需要进一步的讨论与研究.

基于此，本文针对肠易激综合症(irritable bowel syndrome,IBS)与健康对照(healthy control,HC)两组人的静息态fMRI数据，采用ApEn方法与SampEn方法进行分析，计算不同参数r下的ApEn与SampEn的均值差距率并进行对比，探讨哪种算法更适用于fMRI数据的分析.

1 近似熵与样本熵方法

1.1 影像学fMRI数据参数

影像学数据是在被试处于静息闭眼状态(未受到任何刺激，也不执行任何任务)下，通过德国西门子公司的3T磁共振扫描仪采用梯度平面回波成像序列得到的，其参数如下，层厚度5 mm、矩阵大小64×64、回波时间30 ms、重复时间2 s、翻转角度90 °、层内分辨率3.75×3.75 mm2.每个被试的扫描过程需要6 min，共采集180个时间点.在扫描过程中，被试被要求保持清醒并放松的状态，同时使用乌龙头线圈和泡沫垫子固定被试头部避免头动.在本研究中，影像学数据包含16例IBS患者与年龄、性别相匹配的16例HC，其统计学信息如表1所示.

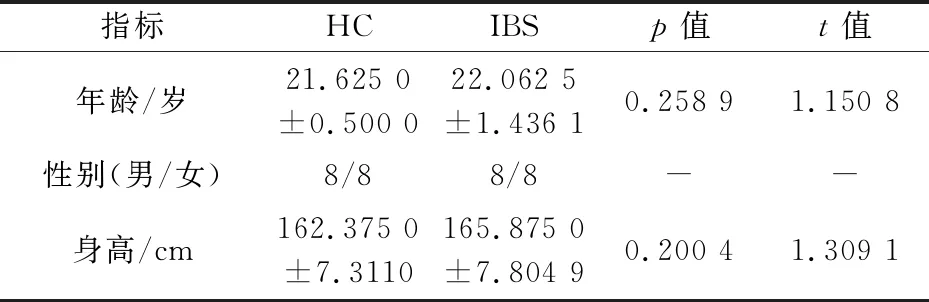
表1 两组被试的人口统计学信息

1.2 影像学的数据预处理

本文对影像学数据的预处理是基于中科院心理研究所开发的DPABI[8]进行的，主要步骤包括：①将fMRI的原始DICOM数据转换为NIFTI数据；②去除体素的时间序列的前10个时间点，保留后170个时间点，避免刚开始扫描仪的不稳定及被试的不适应性等因素对结果的影响；③进行时间层校正，消除层与层的扫描时间的差异；④进行头动校正，去除头动移动大于1.5 mm或者旋转角度大于1.5 °的被试数据，避免在扫描期间头动对结果的影响；⑤进行空间标准化,消除不同个体大脑形态的差异；⑥进行去线性漂移及带通滤波，去除扫描仪及生理活动产生的噪声，提高信噪比，其中带通滤波频率为0.01～0.08 Hz.

1.3 近似熵方法在fMRI中的实现过程

本研究中近似熵的计算是基于MATLAB平台和SPM工具包实现的，经过预处理后的个体脑图像均包含70 831个3.75×3.75 mm3大小的体素，每一个体素对应着一个时间序列，对体素逐个进行ApEn求解，具体步骤如下：

①设预处理后fMRI个体数据的脑图像有n个(即时间序列的长度为n)，全脑有l个体素；

②提取全脑体素的时间序列，矩阵形式如下：

其中，每一列表示一个体素的时间序列.

③针对第t个体素的时间序列X(t)=X(:,t)，将其重构成m=2维向量，向量形式如下：

Xi(t)=(xi(t),xi+1(t),…,xi+m-1(t))T,

i=1,2,…,n-m+1

④计算向量Xi(t),i=1,2,…,n-m+1与所有向量Xj(t),j=1,2,…,n-m+1之间的距离，此时的距离为两向量对应元素差值绝对值的最大值，其计算公式如下：

dij=max|xi+k(t)-xj+k(t)|,

k=0,1,…,m-1

(1)

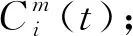
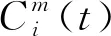
(2)

⑦维数m增加1，重复步骤③～⑥，求得Φm+1(t)；

⑧将求得的Φm(t)和Φm+1(t)作差，其结果即为ApEn(t)，其计算公式如下：

ApEn(t)=Φm(t)-Φm+1(t)

(3)

1.4 样本熵方法在fMRI中的实现过程

本研究中样本熵的计算是基于MATLAB平台和SPM工具包实现的.针对预处理后的个体脑图像，对体素逐个进行SampEn求解，具体步骤如下：

①设预处理后fMRI个体数据的脑图像有n个(即时间序列的长度为n)，全脑有l个体素；

②提取全脑体素的时间序列，矩阵形式如下：

其中，每一列表示一个体素的时间序列.

Xi(t)=(xi(t),xi+1(t),…,xi+m-1(t))T,

i=1,2,…,n-m+1

④计算向量Xi(t),i=1,2,…,n-m与其他向量Xj(t),j=1,2,…,n-m之间的距离，此时的距离为两向量对应元素差值绝对值的最大值，其计算公式如下：

dij=max|xi+k(t)-xj+k(t)|,

k=0,1,…,m-1,i≠j

(4)

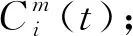
⑥计算所有向量中小于阈值的数目的平均值，记为Φm(t)，其计算公式如下：

水土流失、植被破坏是我国泥石流多发的原因之一。在泥石流等地质灾害高发区，应加大环境保护力度，实行治水、治土和工程防护的综合治理策略，是为治本之策。我国环境综合治理取得了较为显著的效果，应进一步推进。目前主要的几种综合治理模式如表1所示。

(5)

⑦维数m增加1，重复步骤③～⑥，求得Φm+1(t)；

⑧将求得的Φm(t)和Φm+1(t)取对数并作差，其结果即为SampEn(t)，其计算公式如下：

SampEn(t)=lnΦm(t)-lnΦm+1(t)

(6)

1.5 均值差距率

熵用于衡量时间序列的信息发生率，其值的大小反映了系统的复杂性程度.已有研究表明，年龄和疾病特征体现在复杂生理系统的动态复杂度缺失，即熵的降低.因此，IBS患者组与HC组两组人的熵必然会存在差异.本文通过均值差距率v来量化IBS患者组与HC组两组人熵的差异，其值的大小可反映了HC组与IBS组两组人熵的差异程度，其值越大，HC组与IBS组两组人熵的差异越明显，其计算公式如下：

(7)

式(7)中：mHC表示HC组ApEn或SampEn的平均值，mIBS表示IBS组ApEn或SampEn的平均值.

1.6 fMRI数据处理及统计分析

采用步骤1.3的ApEn方法与步骤1.4的SampEn方法计算不同参数r下的两组被试所有体素的ApEn与SampEn，并计算所有被试ApEn与SampEn的全脑平均，每个被试对应一个ApEn与SampEn的全脑平均.采用双样本t检验对HC组与IBS组两组被试的全脑平均ApEn与SampEn进行统计分析(本文认为当p<0.05，两组被试的全脑平均ApEn值与全脑SampEn值存在显著性差异).采用式(7)计算HC组与IBS组的ApEn与SampEn的均值差距率.

为了使HC组与IBS组的均值差距率更加明显，本文同时进行了如下步骤：①对不同参数r下的两组被试所有体素的ApEn与SampEn进行双样本t检验(p<0.05)，筛选出具有显著性差异的体素；②计算具有显著性差异的体素的平均ApEn与平均SampEn；③采用式(7)计算HC组与IBS组的ApEn与SampEn的均值差距率.

根据上述计算结果，可以得到ApEn方法与SampEn方法最优的参数r.计算将该最优参数r下的所有体素的ApEn与SampEn，生成相应的ApEn图与SampEn图并进行平滑处理.采用双样本t检验(GRF校正(p<0.05,差异簇大小>20))进行统计分析，确定两组被试的差异性区域，以验证ApEn方法与SampEn方法的合理性.

2 结果与讨论

2.1 近似熵与样本熵的均值差距率分析

本文采用ApEn方法与SampEn方法计算不同参数r下的所有被试ApEn与SampEn的全脑平均，其值随r的变化曲线如图1所示.采用双样本t检验对不同参数r下的全脑平均ApEn与SampEn进行统计分析，其结果如表2所示.从表2可以看出，ApEn是在r=0.2～0.4下呈现显著性组差异，SampEn是在r=0.15～0.55下呈现出显著性组差异(需要指出，在r=0.1，由于选取r值过小，使得该参数r下存在体素的SampEn值为Inf的情况，显然这是不符合实际的).

图1 ApEn与SampEn的全脑平均随r的变化曲线

表2 两组被试的全脑平均ApEn与SampEn在不同参数r下的统计学差异

采用均值差距率计算公式分别计算不同参数r下的ApEn与SampEn的均值差距率(未经过t检验筛选差异体素)，其值随r的变化曲线如图2所示.为了使HC组与IBS组的均值差距率更加明显，更好地评估ApEn和SampEn的优缺点，经过t检验筛选后的不同参数r下的ApEn与SampEn的均值差距率同样被计算，其值随r的变化曲线如图3所示.从图2、图3可以看出，r=0.1～0.55，SampEn的均值差距率均高于ApEn的均值差距率，其中经过t检验筛选后的效果更加明显，这说明了SampEn方法能更好地区分HC组与IBS组两组被试.

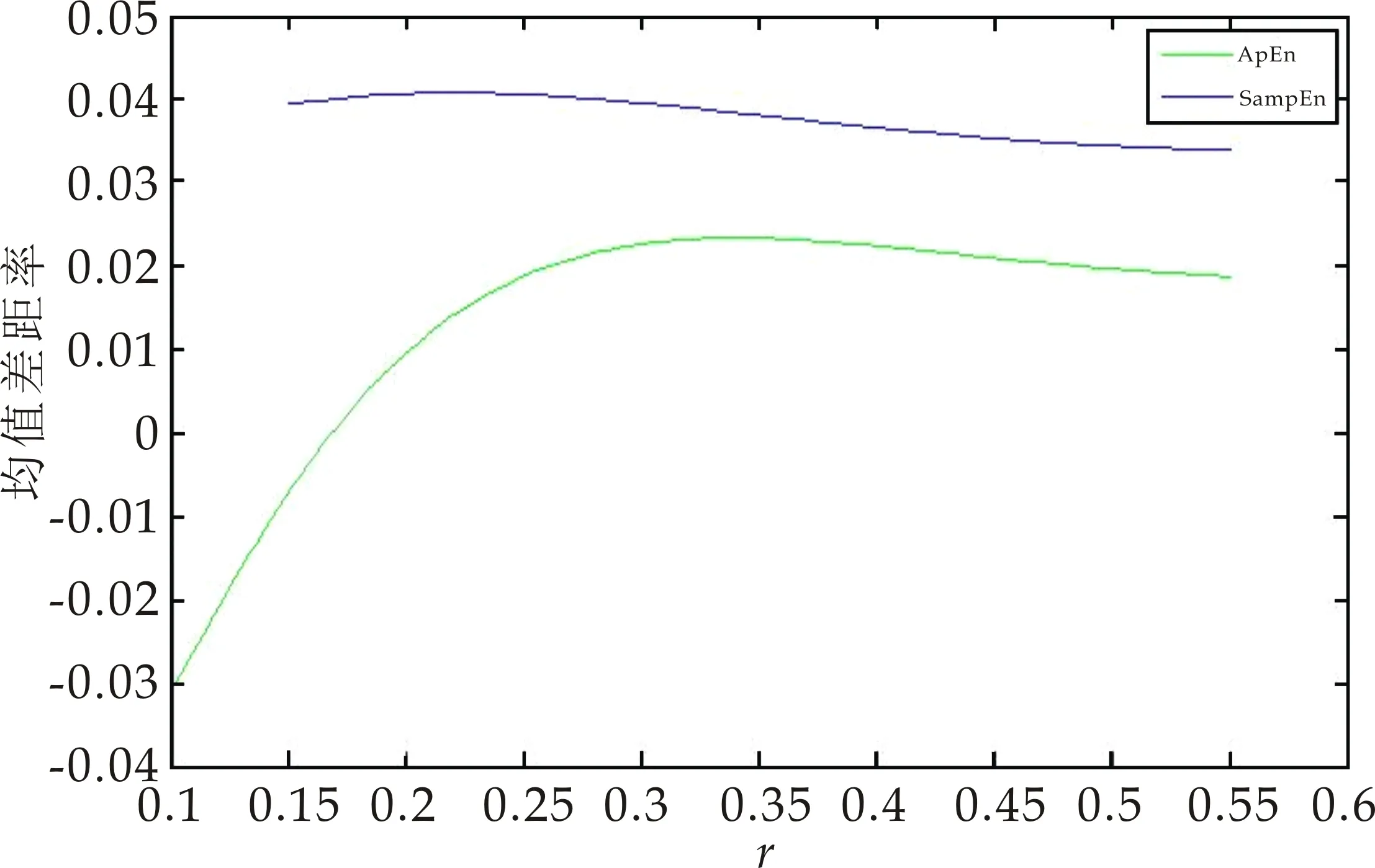
图2 ApEn与SampEn的均值差距率(未经过t检验筛选)随r的变化曲线

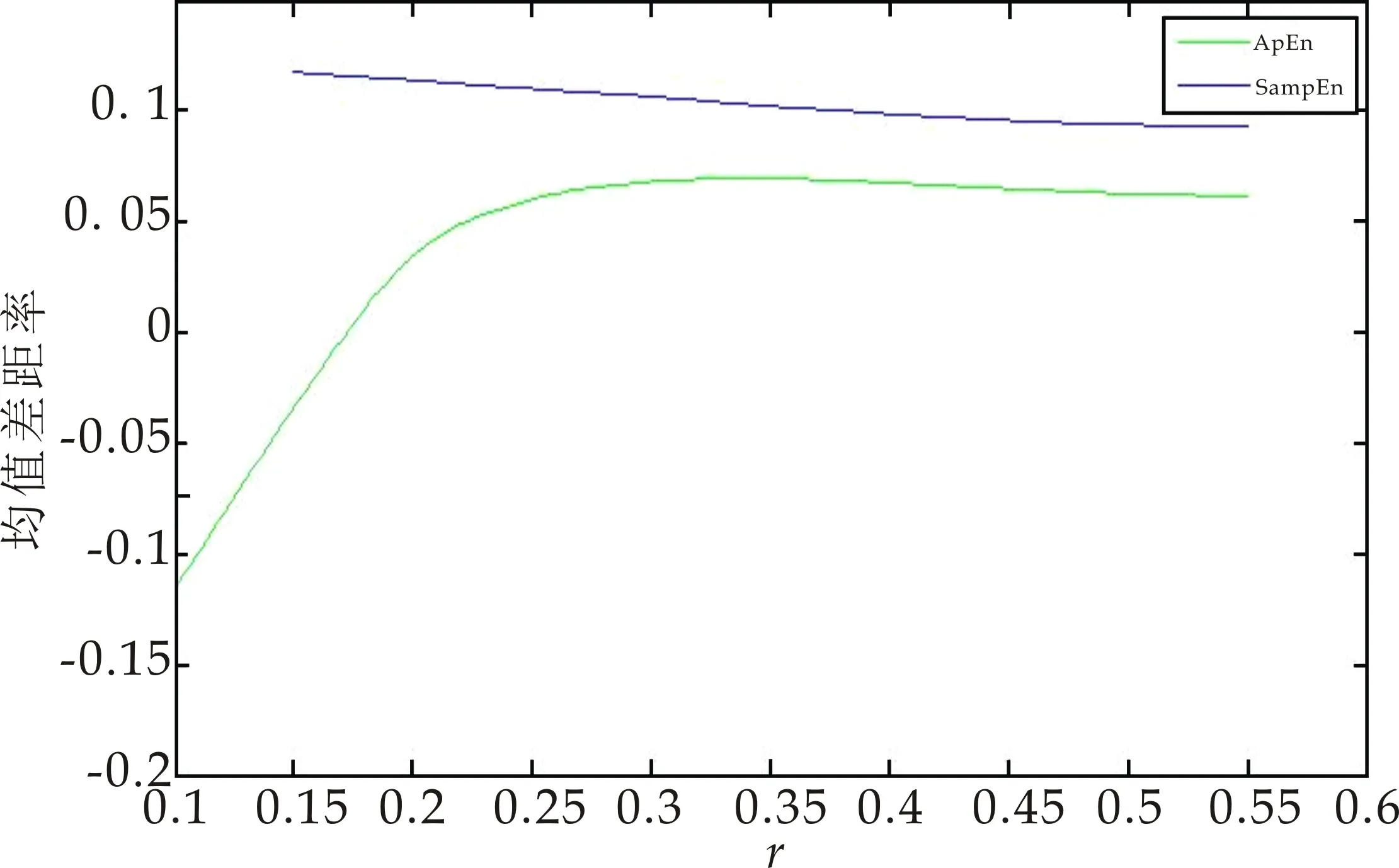
图3 ApEn与SampEn的均值差距率(经过t检验筛选)随r的变化曲线

2.2 近似熵与样本熵算法的运行时间分析

本文对被试所有体素的ApEn与SampEn的运行时间进行了统计，每个被试所需的计算时间如表3所示.从表3可以看出，相比于ApEn，每一个被试所有体素的SampEn的计算时间平均节省28秒，这说明SampEn方法的运行效率更高，这一点在大批量fMRI数据的分析处理中是很有意义的.

表3 一个被试所有体素的ApEn与SampEn的计算时间

2.3 近似熵与样本熵方法确定的差异区域分析

根据上述计算结果，可以得到ApEn方法与SampEn方法的最优参数r.根据Sokunbi等[5]研究中ApEn最优参数r的选取方法，应当选取较为稳定的r值为最优参数，即r的微小变化不会导致全脑ApEn发生突变，因此，本文ApEn最优参数r取为0.25.为保证ApEn与SampEn方法中参数r的一致性，SampEn方法的参数r同样取为0.25.采用双样本t检验对平滑后的HC与IBS两组的ApEn图及SampEn图进行统计分析，结果发现，ApEn差异区域分布如表4所示，而SampEn差异区域分布如表5所示.

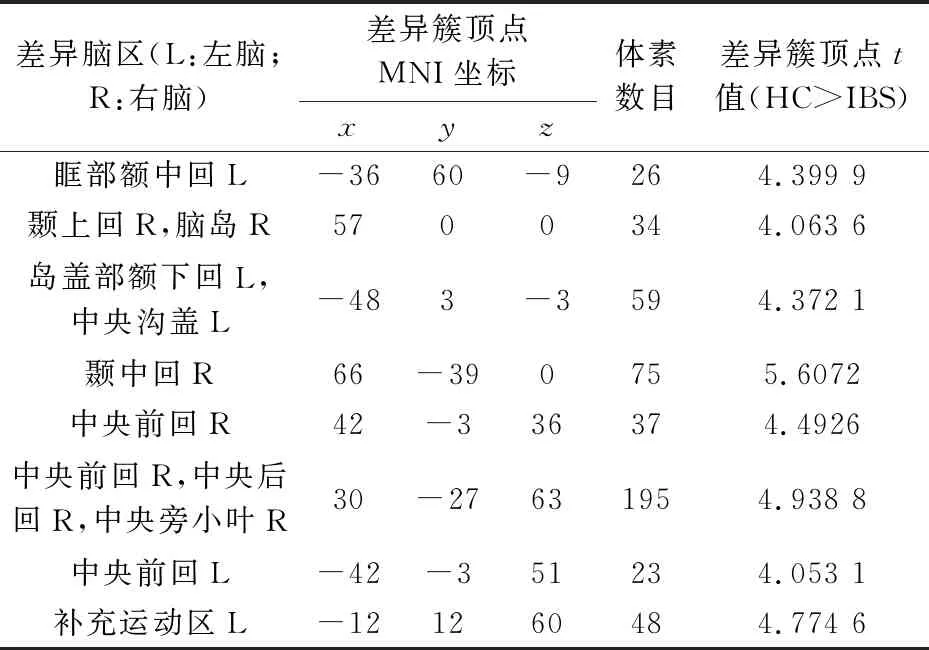
表4 HC与IBS的ApEn差异区域分布

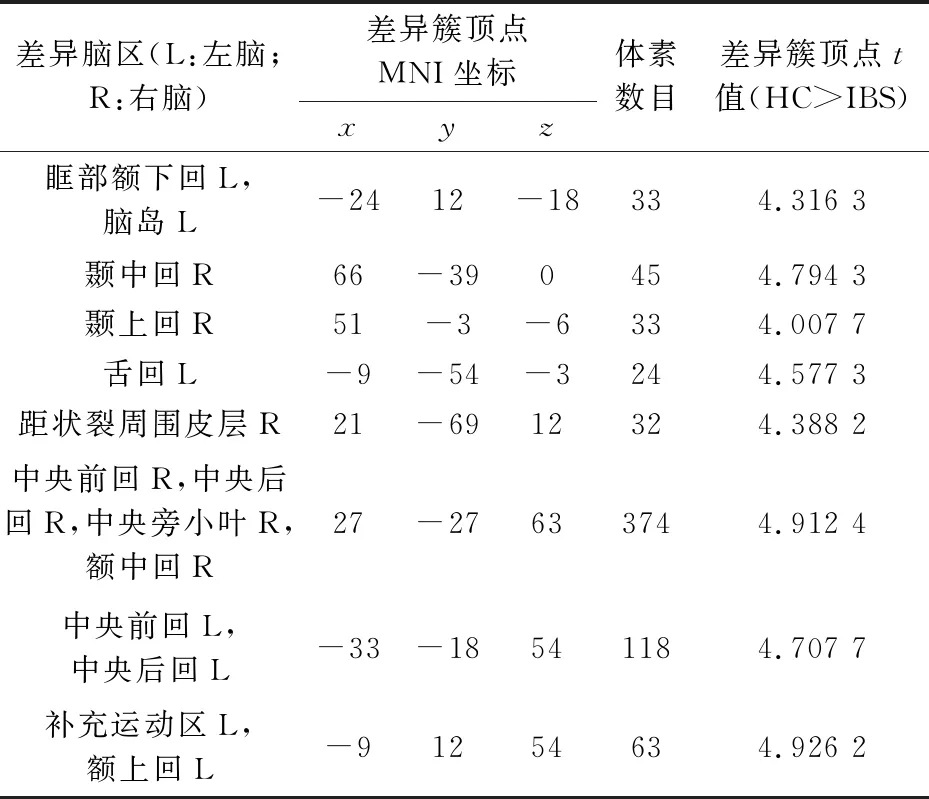
表5 HC与IBS的SampEn差异区域分布

ApEn与SampEn揭示的是大脑功能活动的复杂度大小，其值越大，表示大脑功能活动越复杂[9,10].从表4与表5可以看出，IBS患者与HC的ApEn与SampEn均存在显著性差异，这种差异可能暗示了IBS患者大脑功能活动的异常.本文采用ApEn方法与SampEn方法发现的IBS患者在补充运动区、颞区以及中央旁小叶的异常在以前的IBS或内脏疼痛研究[11,12]中均已被证实.

本文采用SampEn方法发现IBS患者在左侧额上回、右侧额中回及双侧中央后回的SampEn显著小于HC，而采用ApEn方法仅发现IBS患者在右侧中央后回的ApEn显著小于HC.在以前的研究中，Ma等[13]采用低频振幅分析方法发现IBS患者左侧额上回、右侧额中回及双侧中央后回的功能活动存在异常，与SampEn结果一致.这暗示了SampEn能够检测ApEn无法检测的脑体素异常.另外，从表4与表5还可以看出，SampEn方法确定的差异簇大小明显大于ApEn方法.在一定程度上，这说明SampEn方法比ApEn方法更灵敏.

2.4 近似熵与样本熵算法的理论分析

对比ApEn与SampEn方法在fMRI的实现过程可以发现，ApEn方法在计算向量之间的距离时包含了自身，而SampEn方法并不包含自身.一方面，由于包含自身与新信息观点是不相容的，这将导致ApEn方法得到的结果会存在偏差，因此SampEn方法可以得到更加准确的结果，这与本研究中SampEn方法更易区分HC组与IBS组两组被试是一致的；另一方面，由于SampEn方法未进行自身匹配这一步骤，这解释了本研究中SampEn方法的运行时间低于ApEn方法的运行时间.综上所述，SampEn方法可能比ApEn方法更适用于静息态fMRI数据的分析.

3 结论

本文针对HC与IBS两组人的静息态fMRI数据，采用ApEn方法与SampEn方法进行分析，计算不同参数r下的ApEn与SampEn的均值差距率并进行对比.结果发现，随着参数r的增加，SampEn的均值差距率均比ApEn大.同时，SampEn执行单个样本可节约28 s的运行时间，这对fMRI大批数据的分析处理具有重要的意义.因此，相比于ApEn方法，SampEn方法可能更适用于静息态fMRI数据的分析.

需要指出本研究存在的不足之处：①本研究采用均值差距率来区分HC组与IBS组两组被试的差异性，该指标的合理性及有效性仍需更多的fMRI研究来进一步验证；②当前已存在多种熵技术被应用于脑研究[14-20]，但本文仅比较了两种熵在fMRI应用中的均值差距离，在将来的研究中，还需要对更多的熵技术进行深入探讨.