轴向脉冲电流对全塑性铜射流的扭曲不稳定性作用分析

齐文达，向红军，孔庆奕,3，容 烨

(1.河北交通职业技术学院 轨道交通系， 石家庄 050035； 2.陆军工程大学 弹药工程系， 石家庄 050003；3.陆军工程大学 电磁环境效应国家级重点实验室， 石家庄 050003)

被动电磁装甲是一种防御聚能射流的新型装甲类型，它是利用脉冲电流对聚能射流产生诸如箍缩变形、扭曲变形以及电爆炸等破坏作用[1-2]，直接导致聚能射流侵彻能力的降低，从而起到了很好的防御作用[3-5]。被动电磁装甲防护金属射流具有复杂的作用机理，虽然国内外对被动电磁装甲进行了一系列的实验研究，但理论研究还不够充分，难于应用于实际工程。因此，本文针对轴向脉冲电流对射流的扭曲不稳定性，利用磁流体动力学理论、线性扰动理论和叠加原理，建立了全塑性金属射流在轴向脉冲电流作用下的扭曲扰动方程，对轴向脉冲电流对全塑性铜射流的扭曲不稳定性作用机理进行了研究。

1 全塑性铜射流运动变形规律

(1)

式(1)中，Vtip和Vtail分别为金属射流速度头部和尾部速度，当到达t时刻时，由于自由拉伸的作用金属射流的长度由L0变成了L，即

(2)

得到t时刻金属射流初始轴向应变率为

(3)

同时，由于破甲弹药型罩产生的射流不可能是完全对称的，即存在非对称扭曲变形，当有脉冲电流通过具有非对称变形的射流时，可进一步促进射流的扭曲，破坏射流在轴向的连续性，从而降低甚至消除射流对装甲的侵彻能力。

2 射流扭曲不稳定增长率研究方法

由于破甲弹炸高小，而且铜射流在被动电磁装甲中飞行距离非常短，在无轴向脉冲电流作用下，在很短时间内铜射流微小变形几乎没有变化，为此把铜射流产生的扭曲变形看作小扰动，根据叠加原理，可假定铜射流形状为无限长圆柱体与微小扭曲扰动变形的叠加，圆柱铜射流上的脉冲电流不会引起铜射流变形，仅增加了铜射流的体压力，处于平衡状态，为此铜射流的最终变形可看作由圆柱铜射流自由拉伸运动和受扰后电磁力引起的扭曲变形构成。小扰动就可以用本征函数表示，对于平衡态和在边界条件确定的情况下，本征函数具有唯一性，它与初始扰动的给定无关[6-7]。本文认为铜射流处于平衡态时为轴对称圆柱铜体，扰动方程可以用指数形式表示为

ξ(r,θ,z)={ξr(r),ξθ(r),ξz(r)}ei(mθ+kz)+st

(5)

式(5)中，m和k分别为角向波数和轴向波数，m=1时为扭曲扰动；s=Γ+iω，Γ表示不稳定增长率，Γ大于0和小于0分别表示失稳和致稳；ω为扰动的频率；ξr、ξθ和ξz表示扰动振幅分量。利用扰动方程把三维运动控制方程化简为一维，大大简化方程的求解。

3 全塑性铜射流扭曲不稳定增长率

为了便于分析，假设铜射流不可压缩、电阻率常数。全塑性铜射流在轴向脉冲电流作用下的运动控制控制方程为

▽·V=0

(6)

(7)

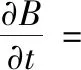
(8)

式(7)中J为偏应力张量。式(6)～(8)分别为不可压缩方程、运动方程和磁扩散方程。

假定铜射流某一时刻平衡态时的体压强、速度、电流密度和磁感应强度分别为P0、V0、J0和B0，所对应的扰动量用P1、V1、J1和B1表示，可得

P1、V1、B1、J1、1∝exp(st+imθ+ikz)

(9)

式(9)中，

V=V0+V1，P=P0+P1，B=B0+B1，

J=J0+J1，=0+1

(10)

令扰动造成的位移矢量为

ξ=r-r0

(11)

它为一阶小量，其中r和r0分别为铜射流变形后和平衡时的铜射流微元位置，这样有

(12)

将式(9)、(10)代入理想铜射流运动控制方程式(6)～(8) 中，可得全塑性铜射流一阶线性扰动运动控制方程为

(13)

(14)

(15)

在柱坐标系下

(16)

偏应力张量与应变率成正比，在柱坐标条件下

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

由于脉冲电流含有各种高频成分，因此脉冲电流会在铜射流表面产生趋肤效应，那么圆柱铜射流上的电流密度J0为[10-11]

(25)

式(25)中，J0z为电流密度在坐标z向分量；J0为一阶贝塞尔函数。由此可得圆柱铜射流上磁感应强度B0为

(26)

式(25)中，B0θ为磁感应强度在坐标θ向分量；eθ为坐标θ方向上的单位矢量。由式(23)～(26)可以得

(27)

数值计算时，取系统电感L=1 μH、系统电阻R=15 mΩ、C=2 mF和U0=20 kV，在脉冲电流的上升沿阶段，利用数值计算求解方程式(27)可得到全塑性铜射流扭曲不稳定增长率Γ随时间t、轴向波数k和屈服极限Y的变化规律，如图1所示。

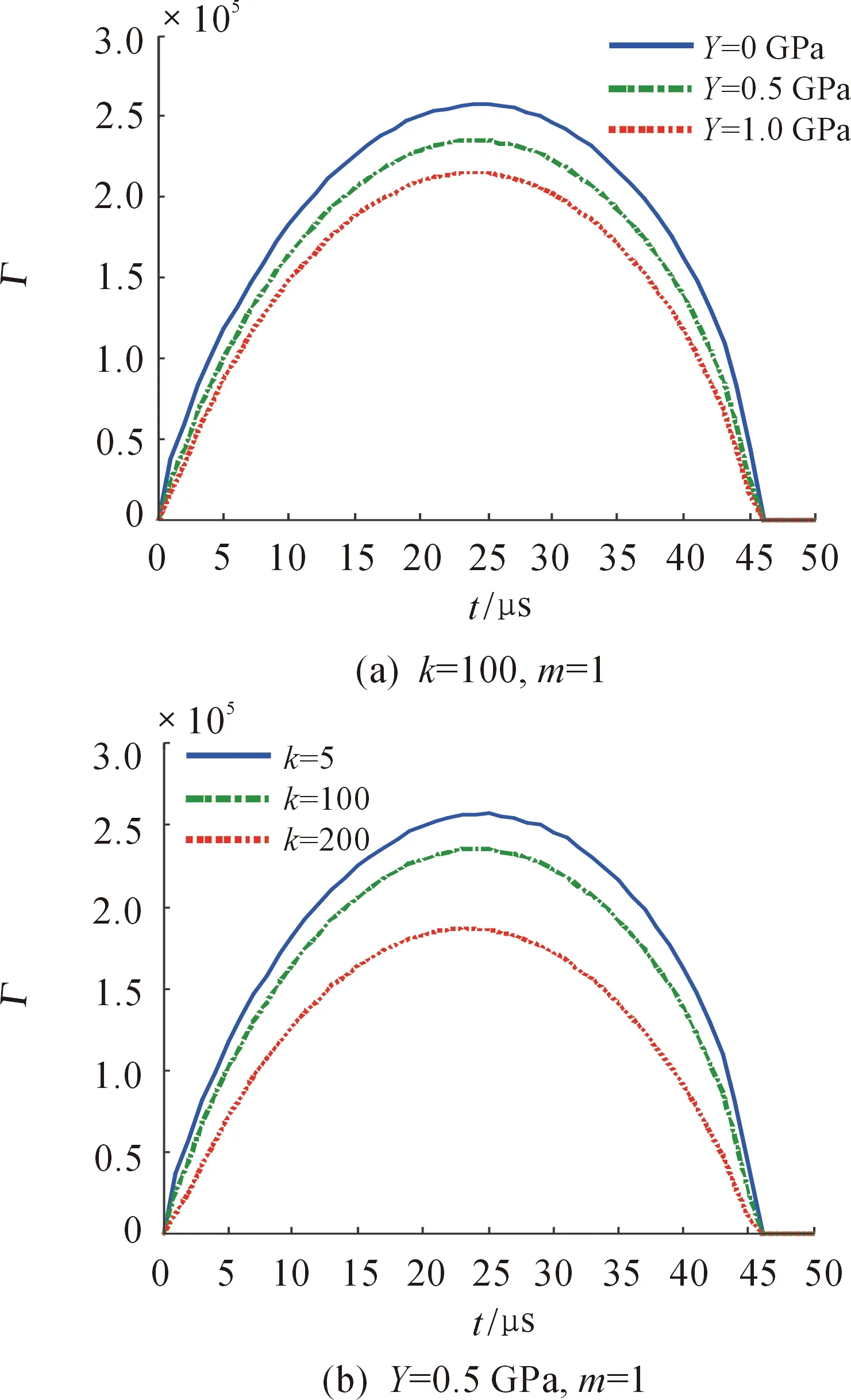
图1 扭曲不稳定增长率

由图1可知，全塑性铜射流扭曲不稳定增长率随着屈服极限Y和轴向波数k的增加而减少。在脉冲电流上升沿阶段，全塑性铜射流扭曲不稳定增长率随时间的增加呈现出先增大后减小的现象，这是由于在脉冲电流放电开始阶段，脉冲电流更多的集中在金属射流扭曲变形的内表面，而当脉冲电流达到峰值附近时，脉冲电流波形逐步变平，频率降低，脉冲电流在铜射流截面上趋向于均匀分布，并最终造成了扭曲不稳定增长率趋于0，所以脉冲电流在铜射流截面上的均匀分布不会引起全塑性铜射流的扭曲不稳定性。

4 扭曲不稳定性作用试验

由于高速铜射流的扭曲形态难于控制、试验过程极其复杂、成本高，而且难于实现定量试验，为了验证破甲弹产生的聚能铜射流在轴向脉冲电流作用下的扭曲不稳定性，设计了一种静态模拟试验装置，利用扭曲铜丝进行了静态模拟定性试验。

本试验采用中国科学院电工所生产的高压脉冲充放电装置。开关采用三电极火花间隙开关，用于测量电流的装置罗夫斯基线圈的标定参数为：11 025.69 A/V。

扭曲试验装置两侧板采用环氧树脂板作为固定板，两固定板外侧固定了接线柱，用于把铜丝与正负极电源线相连，板间距为200 mm。

静态扭曲实验如图2所示。图2(a)中当充电电压为5 140 V时，通过铜丝的峰值电流为50 kA，铜丝直径为1.75 mm，图2(b)中①的铜丝为初始状态，图2(b)中②的铜丝为脉冲电流放电后的状态，对比图2中上下铜丝的形状可知，脉冲电流对铜丝产生了扭曲作用力致使铜丝进一步变形。由线性不稳定理论求得的铜射流扭曲不稳定增长率随时间的变化曲线可知，轴向脉冲电流一定会引起扭曲铜射流产生进一步的扭曲变形，与试验结果相一致。

图4 静态扭曲实验

5 结论

1) 脉冲放电电流能够对具有初始扭曲扰动的金属射流产生进一步扭曲变形，而且只要电流足够大，被动电磁装甲就能够降低金属射流甚至消除金属射流对装甲的侵彻能力。

2) 脉冲电流在射流上均匀分布不会引起扭曲不稳定性。由于脉冲电流在金属射流上分布趋于均匀分布，造成了在脉冲电流上升沿金属射流扭曲不稳定增长率先增加后减少并最终趋向于0的现象。

3) 全塑性金属射流的不稳定增长率随轴向波数和屈服极限的增加而减小。随着温度的升高，全塑性金属射流屈服极限会随之下降，这时金属射流的不稳定性规律会逐渐接近准流体的不稳定性规律。

4) 静态模拟定性实验的结果证实了轴向脉冲电流能够引起扭曲变形射流的进一步扭曲变形。由于射流两端为自由端且屈服极限更低，实际金属射流扭曲变形要比实验中铜丝扭曲变形更加显著。