课堂练习的“三注重”
吴熙

【摘 要】小学数学课堂练习,要做到“三个注重”:注重针对性,注重扩展性,注重趣味性。让课堂练习真正成为学生理解知识、运用知识、发展智慧、形成能力的手段。
【关键词】小学数学;课堂练习;三注重
新课标中明确数学教学要实现“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”。其中练习就是培养和发展学生数学能力的一个重要手段。而课堂练习又有别于其他练习,课堂练习即是检测学生掌握新知最直接的手段,也是帮助老师及时调整教学内容的方向标,更是学生回去完成其他练习的范式和参考。在现实教学中,很多教师却不把课堂练习设计当一回事,只是简单的完成课后的配套练习或者现成课件中的补充练习,无设计而言。于是课堂练习的呆板、杂乱、量大便成了常态,学生做起来索然无味,大大降低了教学质量。如何在有限的课堂时间内,既让低差生“吃的下”,又让优等生“吃的饱”,最大限度的发展学生的智慧,形成能力呢?这是需要教师精心设计练习,努力做到三个“注重”。
一、注重练习目标的针对性
课堂练习首先是教师针对教学的重点难点设计的教学活动,是检查学生知识、技能、方法掌握的重要手段。因此,教师在准备课堂练习时,应该明确练习的目的,针对不同层次的学生设计练习的内容和练习的序,让不同层次的学生都能有所收获,并且有能力向上跳一跳,挑战更高层次的练习,思维得到相应的发展。
1.不用跳够得着
课堂练习作为教学目标达成的一种有效手段,巩固基础是起点。因此,练习的设计必须把握准教学的目标,从而确定练习的起点,在巩固知识基础中,促进学生的思维发展。
例如,在教学“三角形的面积”时设计的第一层次练习:
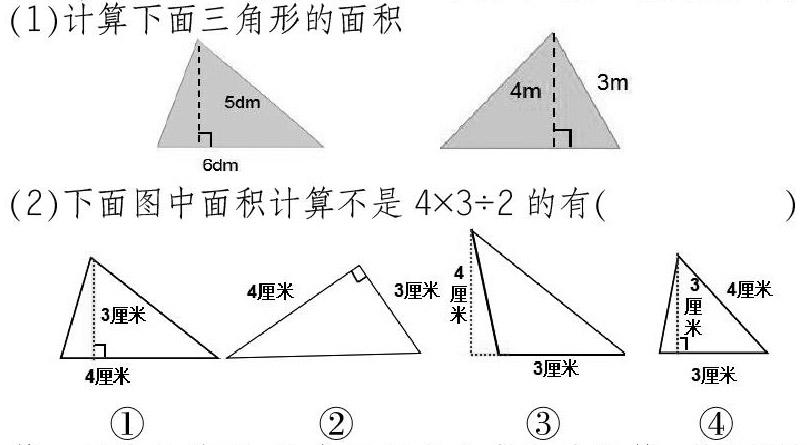
(1)计算下面三角形的面积
(2)下面图中面积计算不是4×3÷2的有( )
第一层次的练习,重在于利用公式正确计算,巩固面积公式的计算方法,寻找三角形中相对应的底和高。除了必要的计算练习,有限的课堂时间中,课堂练习也可一改往常相对单一的解题方式,以选择题的方式,把不同形状三角形的底和高作为选项让学生去思考、辨析,淡化了繁琐、重复的计算,更突出考察“把握三角形中底、高相对的关系”这一核心目标。这样的练习,兼顾到不同学生的发展需求,帮助学生从“会”过渡到“熟”。
2.跳一跳够得着
学生理解、运用知识必须经历一个由浅入深、由易到难的过程,在学生已经掌握基础知识的基础上,设计有一定思维含量的练习,提高学生的思辨能力。
例如,在教学“三角形的面积”时设计的第二层次练习:
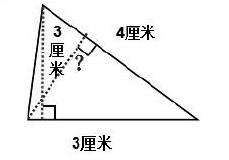
(1)已知一组的底是3厘米,高是3厘米,另一个底是4厘米,求另一个高是多少?
(2)已知平行四边形的底是6分米,高4分米,求涂色部分的面积。
(3)已知平行四边形的底是6分米,高4分米,求涂色部分的面积。(课件依次出示:5个不同形状的等底等高的三角形)
第二个层次的练习:重在计算发现等底等高的三角形和平行四边形之间的关系,以及等底等高三角形面积的不变性。已知三角形的一组底和高,要求另一组的高或者是底,是教学的难点,也是学生的易错点。这样的递进练习,大部分学生跳一跳是能够解决的,不仅能感受到图形变化规律的奇妙,在老师的适当鼓励下,学生也能感受到学习数学的成就感。
3.跳几跳够得着
练习设计的好坏,直接体现在练习的层次性中。在循序渐进的练习中,变式的练习更能促进学生创造性思维的发展,促使学生进一步从“熟”到“活”,使知识结构更好的往结构化发展,优化所学知识。
例如,在教学“三角形的面积”时设计的第三层次练习:
(1)图形变变变
已知平行四边形的底是6分米,高4分米,求涂色部分的面积。(课件依次出现下图)
(2)比较下列涂色部分图形的面积
第三个层次的练习:重在启发学生利用“等底等高的三角形面积相等”解决问题。在变与不变中,引导学生用同底等高的三角形面积相同来解决问题。在第二层次的练习的基础上,继续改变三角形的形状,乃至个数,在变中寻找不变,突出“等底等三角形面积的不变形”。这样的练习,需要学生具备清晰的逻辑思维能力,是一种较高难度的练习,但对于学生的思维能力的训练有着重要的作用。
三个层次的设计,由易到难,拾阶而上,为学生提供思考的阶梯,不同层次的学生都有不同的发展,即能让学困生夯实基础,又启发中等和优生的思考,一节课做到下保底,上不封顶。
二、注重练习内容的扩展性
在教学实践中,教师往往存在简单处理“练”的问题,比如,练得习题不够精选,随意性大,甚至在习题课上只是简单的就题讲题,让学生依葫芦画瓢的订正。练习设计中,教师应该精选练习素材,打通知识点的隧道,增加知识的深度,扩宽知识的宽度,实现知识的融会贯通。
1.易混、易错的改进策略
学生在学习过程中,难免会出现对知识理解的偏差。教师在设计练习时要抓住学生对知识的薄弱点下功夫,避免思维定势形成错误。除了教师提前预测学生的错误,提前暴露“错处”,让学生防范于未然的避免。还有一种方式:教师可以将这些易错点和学生的前知识练习起来,将易错的概念置于更大的知识体系中,站在高观点理解,实现知识的结构化。
例如,在教学“倒数的认识”时,倒数的意义和找倒数的方法是学生易混淆点。当问倒数的意义是什么时,学生给出的回答往往是“分子和分母相互颠倒”,而不是“乘积是1的两个互为倒数”。在课堂中,为了让学生真正了解倒数的意义,我就设计了两道扩展性的练习,将倒数的知识与数轴、直角坐标系联系起来,挖深知识的深度扩展知识的广度。
练习一:找倒数,并指出倒数在1的什么位置。
将倒数的知识和数轴知识联系起来,课件中依次出现,,3,4这四个数,借助想象,学生思考这些数的倒数和1的位置关系,再逐一出示答案。借助一维的数轴模型,学生能直观的感受到一个数和它倒数(除了1)均分布在1的两侧,但乘积始终为1。接着借用数轴模型,学生还可以进一步理解真分数的倒数都小于1,假分数的倒数大于等于1。
练习二:借助圖形,将一组组倒数描在直角坐标系中。
最后,沟通倒数和数对间的联系,通过在方格图中描点连线的方式,得到反比例函数的一支曲线。尽管学生还未研究过反比例函数,但借助直观体验,这种此消彼长的关系岂不更能深深的印入学生的思维中。再借助这些面积是1的长方形,学生总结出只要长方形的面积是1,无论长有多长,宽有多短,但终究存在,永远也不会是0。
2.一题多练的策略
数学练习,不是静止地、孤立地的解决一个问题,而是应该加以研究,通过一题多变,克服思维定势的影响,拓展学生的解题思路,培养学生思维的灵活性和深刻性。
例如,在人教版五年级下册《探索图形》的配套练习中,有这样一个问题:
下面是用8个小正方体拼成的,如果拿走其中的1个,
它的表面积会发生变化吗?
借助情境和原有的知识经验的基础上,学生会总结出拿走上面一层中的任何1个正方体,拿走的小正方体露在外面的3个面消失,但又会出现3个新的面来弥补(也有的学生能用平移的观点来解释),它的表面积是不变的。到此,题目中呈现的问题似乎解决了,但是如果教师深入挖掘,更能激发出本题的本质,启发学生的思考。
进一步引导学生思考“如果拿走2个,表面积是否发生变化?如果拿走3个,表面积是否发生变化?为什么拿走1个、2个、3个表面积的变化不一样呢?”在学生原有问题的基础上,挖掘的新的问题,实现一题多变,一题多练,学习走向深入,真正实现减负提质。
总之,在小学数学中,课堂练习是教学的核心内容之一,也是培养和发挥学生智慧和能力的关键。因此,教师要充分发挥自己的教学机智,有效整合和挖掘知识内容,从而实现有效高效的教学。

