可逆式机组导叶和进水球阀协联关闭规律研究

(1.湖北省水利水电规划勘测设计院，湖北 武汉 430000；2.调峰调频发电公司，广东 广州 510630)

1 引 言

抽水蓄能电站广泛采用一洞多机的布置格局，如惠州抽水蓄能电站采用一洞四机的布置格局，浙江桐柏抽水蓄能电站采用两洞四机的布置格局，白莲河抽水蓄能电站采用一洞两机的布置格局，江苏沙河抽水蓄能电站采用一洞两机的布置格局等。由于抽水蓄能电站的水头一般较高，管线较长，通常采用埋藏式管道，采用一条引水主管道通过岔管连接多台机组的一洞多机供水，一定程度上可节约电站建设的成本，较为经济。但是使用一洞多机布置格局，可能出现位于同一水力单元的机组间的互相影响，并且甩负荷的情况将更加复杂[1]。相对于其他工程措施而言,优化导叶关闭规律是处理水力过渡过程问题的最优方法[2]。因此，为使抽水蓄能电站能够经济可靠地运行，通过优化导叶关闭规律和进水球阀关闭规律，来解决抽水蓄能电站并行可逆机组在水力过渡过程中出现的问题，具有重要意义。

近些年来相关单位和学者对抽水蓄能电站导叶关闭规律作了深入的研究。杨建东[3]认为水轮机工况下对导叶关闭规律优化的重要影响因素包括水轮机机型、调保参数控制值以及调压室类型和布置方法等，从而提出了两段折线关闭规律，主要是依据实际工程经验和水锤传播规律来判定折线关闭规律的折点位置。Wylie,E.B.等[4]以简单管道的研究为例，阐述了一种确定最优关闭规律的新方法——反演法，并将这种新方法推广使用到复杂输水系统。但是，难以实现最优关闭规律的计算。张健等[5]提出了三段式折线关闭规律，三段折线关闭规律与两段折线关闭规律的区别在于导叶关闭中间段引入延时段，通过引入延时段避免了因导叶关闭和机组转速上升共同作用引起的抽水蓄能电站可逆式机组流量变化，尾水管水锤压力能得到有效的控制，江苏沙河抽水蓄能电站已经运用了这种关闭规律。于桂亮等[6]对一洞两机抽水蓄能电站的导叶关闭规律进行了研究，分别分析对比三种典型关闭规律：直线关闭规律、两段式折线关闭规律和延时直线关闭规律，对比结果表明前两种关闭规律的缺陷能够通过延时折线关闭规律得以显著的改善，蜗壳进口最大压力能得到明显控制。刘立志等[7]研究了延时直线关闭规律，对比分析使用延时直线关闭规律和两段折线关闭规律分别进行水力过渡过程计算的结果，发现前者能有效地降低机组转速最大上升率。

优化关闭规律和关闭时间是水力过渡过程计算的主要控制因素。但上述研究没有结合导叶关闭状态研究对调保参数的影响。本文对清远抽水蓄能电站在最大水头下，4台机组同时甩全负荷，其中1号机组导叶拒动，球阀关闭的工况进行分析，探讨了不同导叶关闭规律、进水球阀关闭规律和导叶关闭状态对抽水蓄能电站水力过渡过程的影响，以保证抽水蓄能电站机组在最不利工况下的安全运行。

2 水力过渡过程分析模型

清远抽水蓄能电站输水系统采用了首部式开发、一洞四机、一级竖井加一级斜井的布置格局。进行水力过渡过程计算时的管网系统物理模型见图1，图1中J25、J24、J23、J22分别代表1号机组、2号机组、3号机组、4号机组；J30代表尾水调压室。

2.1 控制方程

任意圆管中水流的运动控制方程组包括连续方程和运动方程，见式(1)、式(2)。

连续方程：

(1)

运动方程：

(2)

式中H——以某一水平面为基准的测压管水头，m；

Q——断面的平均流量，m3/s；

A——圆管截面面积，m2；

D——圆管直径，m；

a——水击波传播速度，m/s；

t——时间，s；

g——重力加速度，m/s2；

x——沿管道轴线的位移，m；

图1 管道参数计算简图

θ——管道轴线与水平面夹角，(°)；

f——Darcy-Weisbach沿程摩阻系数。

2.2 特征线法

特征线法是目前用于计算输水系统水力瞬变的所有数值计算方法中最为常见的一种。特征线法可用于处理各类复杂的水力边界的问题，分析各种输水系统的水力瞬变，而且相比其他差分法，具有较好的精度[8-9]。

式(1)和式(2)是一组拟线性双曲型偏微分方程，抽水蓄能电站输水系统过渡过程计算分析，主要是计算求解上述方程中的流量Q和水头H。

2.3 节点边界条件

为了求解边界节点的瞬变参数，需补充边界条件如下。

2.3.1 机组节点边界条件

水轮发电机组两侧节点相距较短，因此在瞬变工况连续方程仍然成立，故可知：水轮发电机组两侧节点的断面平均流量与水轮机发电机组中间任意节点的断面平均流量相等。

不考虑发电机组的局部水头损失和流速水头的变化，由根据能量方程可知：水轮发电机组两侧节点的测压管水头与水轮机发电机组中间任意节点的测压管水头相等。

2.3.2 尾水调压室节点边界条件

任何结构型式的调压室均不能对压力管道或尾水管道中的水击波产生完全反射，因此，在进行抽水蓄能电站水力机械系统过渡过程计算时，应作为一个水力元件参加整个水力系统的瞬流计算。一洞四机条件下，阻抗式调压室的边界条件如下：

不计节点局部水头损失，则

H1+H2+H3+H4=H5+HD

(3)

假定该节点处水流满足连续方程，则调压室流量连续方程为

Q1+Q2+Q3+Q4=Q5+QD

(4)

式中HD——调压室水位，m；

QD——通过连接管进、出调压室的流量，m3/s；

H5——水流通过调压室之后的测压管水头，m；

Q5——水流通过调压室之后的断面平均流量，m3/s。

Q和H的下标1、2、3、4是指一洞四机条件下，各水轮发电机组一侧节点的值，即H1是指第一台水轮发电机组上(或下)侧管道节点的测压管水头值。

3 现场试验与数值模拟对比分析

依托实际抽水蓄能电站进行现场甩荷试验，并分别结合数值计算和现场试验比较分析导叶关闭规律对调保参数的影响规律，进而验证数值模型对抽水蓄能电站并联运行可逆式机组水力过渡过程模拟的可靠性。

3.1 电站的基本情况

清远抽水蓄能电站位于广东省清远市清新县太平镇境内，上、下水库同属于北江一级支流秦皇河。电站总装机容量1280MW，输水系统采用一洞四机方案布置。上、下水库水位差约475m，输水系统长度约为2779m。

导叶关闭规律的优化选择需要满足的调保参数控制条件为：机组最大转速上升率不超过45%；蜗壳进口压力不超过780m水柱；尾水管进口压力不低于12m水柱。

3.2 现场试验

水轮机甩负荷时导叶采用两段折线关闭规律，第一段采用快关(时长约2.41s)，折点为相对开度为73%的位置；第二段为慢关(时长约69.1s)。同时关闭导叶与进水球阀，进水球阀关闭时长为70.5s，见图2。

图2 水轮机甩负荷时导叶、进水球阀关闭规律

对4台机组同时进行了甩全负荷试验，试验时上游水位为602.76m、下游水位为122.67m，净水头为480.09m。试验结果见表1。由表1可知，ⓐ转速变化率满足调保要求，4台机组转速变化趋势基本保持一致，最大转速变化率为37.5%；ⓑ蜗壳水压均能满足调保要求，4 台机组蜗壳水压振动周期、波形衰减趋势一致，蜗壳最大水压力为686.5m；ⓒ尾水管水压力也能满足调保要求，4 台机组的尾水管水压波形变化也趋于一致，尾水管最小水压力约为44.8m。

表1 四台机组甩全负荷时计算结果与实测数据对比

3.3 模型验证

对比分析表1可知：蜗壳进口最大水压力、尾水管最小绝对压力现场试验的实测值与数值计算结果误差保证在5%以内，而机组最大转速上升率的数值计算误差控制在10%以内。因此，本文数值方法对抽水蓄能电站并联运行可逆式机组大波动过渡过程模拟可靠。

4 工程算例的数值模拟分析

根据比较不同水位和运行组合的计算结果可知，该水电站蜗壳末端最大动水压力、尾水管最小压力和机组最大上升率出现在如下工况：最大水头502.73m下，4台机组同时甩全负荷，其中1号机组导叶拒动，2号～4号机组导叶正常关闭，球阀关闭。因此，为使蜗壳末端最大水压力、尾水管最小绝对压力和机组最大上升率均保有合适的安全裕度，对该控制工况进一步计算分析导叶关闭规律和进水球阀关闭规律的影响。

4.1 导叶直线关闭，进水球阀直线关闭

抽水蓄能电站可逆式机组导叶直线关闭时,导叶全行程关闭时间约为20s，若为大容量可逆式机组需30s以上。因此在水轮机正常工况下，采用导叶直线关闭规律，并对导叶关闭时间在40～120s设置多个计算工况，见图3。同时，对进水球阀关闭规律采用0.5s延时、70s直线关闭，见图4。针对不同的导叶关闭时间配合使用相同的进水球阀关闭规律。

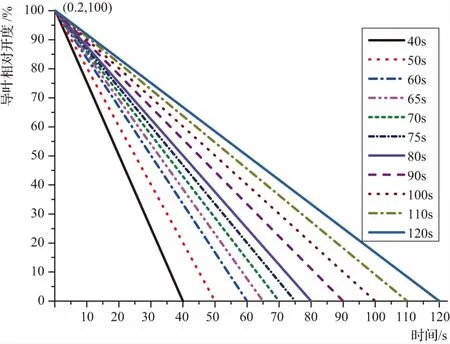
图3 导叶直线关闭规律

图4 进水球阀70s直线关闭规律

图5 采用不同直线关闭时间时导叶正常关闭机组尾水管最小绝对压力结果

在水轮机正常工况下，导叶关闭规律采用直线关闭规律时，水力过渡过程计算结果见图5～图7。由图5可知：当机组导叶采用40～120s直线规律关闭，进水球阀采用70s直线规律关闭时，导叶正常关闭机组(2号、3号、4号机组)的尾水管最小绝对压力变化趋势一致，尾水管最小绝对压力随导叶关闭时间增大而增大，但是增加率随导叶关闭时间不同而不同，在导叶关闭时间为70～80s时，尾水管最小绝对压力随导叶关闭时间增大而减小；在导叶关闭时间达到100s之后，尾水管最小绝对压力趋于一个定值。

图6 采用不同直线关闭时间时导叶正常关闭机组转速最大上升率结果

图7 采用不同直线关闭时间时导叶拒动机组调保参数极值结果

出现这种现象的原因可能在于，在非恒定流情况下，尾水管真空值为

(5)

式中HB——尾水管真空值，m；

Hs——静力真空值(位置真空值)，仅随机组安装高程和下游水位变化,m；

ΔHB——尾水管内水锤压力减少绝对值，m；

由图6可知：正常关闭机组(2号、3号、4号机组)的机组转速最大上升率变化趋势相同，机组转速最大上升率随导叶关闭时间的增大而增大，但是在导叶关闭时间达到60s以后，机组转速最大上升率的增大趋势渐缓，因此要使机组转速最大上升率满足调保参数控制值的要求，应该采用合理的较短的导叶关闭时间。机组最大转速上升率随导叶关闭时间的缩短而减小的原因主要包括：ⓐ导叶有效关闭时间越短，机组就越快通过水轮机运行区域进入制动区域，机组转速上升历时就越短，上升率就越小；ⓑ机组转速上升率近似与导叶关闭有效时间的平方根成正比。于桂亮[6]、刘晓丽等[10]和张东升[12]研究导叶关闭规律对抽水蓄能电站过渡过程的影响时，得到了类似结论。

由图7可知：导叶拒动机组(1号机组)的转速最大上升率随导叶关闭时间变化不明显，但是在导叶为40～120s的直线关闭规律时，机组转速最大上升率都能满足调保参数的控制要求，拒动机组与正常关闭机组的转速最大上升率随导叶关闭时间变化规律基本一致；导叶拒动机组(1号机组)的尾水管最小绝对压力值随导叶关闭时间的延长而增大，在导叶关闭时间为100s时，尾水管最小绝对压力值出现了折点，但是没有改变其变化趋势，尾水管最小绝对压力值在导叶关闭时间为40～50s时，不能满足尾水管最小绝对压力的控制要求。出现的原因与图5、图6相似。但是拒动机组的尾水管最小绝对压力比正常关闭机组小，其转速最大上升率比正常关闭机组大。

总之，在导叶直线关闭总时间为40s时，导叶正常关闭的甩负荷机组的各调保参数均满足控制要求，且有较大裕度；但对于导叶拒动的甩负荷机组，当采用导叶直线关闭规律且总时间大于60s时，尾水管最小压力才满足控制值要求。

4.2 导叶直线关闭，进水球阀两段折线关闭

采用4.1中相同的导叶关闭规律，但进水球阀采用两段折线关闭规律，总关闭时长为75s，采用“先快后慢”的关闭方式，关闭时间为15s时，调整进水球阀关闭速率，进水球阀关闭规律见图8。

图8 进水球阀两段折线关闭规律

图9 采用不同直线关闭时间时导叶正常关闭机组尾水管最小绝对压力结果

图10 采用不同直线关闭时间时导叶正常关闭机组转速最大上升率结果

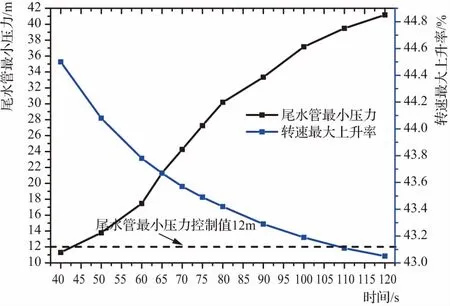
图11 采用不同直线关闭时间时导叶拒动机组调保参数极值结果

在水轮机工况下，导叶关闭规律为直线关闭规律时，计算结果如图9～图11所示。由图9可知：尾水管最小绝对压力的变化趋势与图5类似，总体数据均相对较大。因此，进水球阀采用折线关闭较直线关闭有利于提高抽水蓄能机组尾水管最小绝对压力。

由图10可知：机组最大转速上升率的变化趋势与图6类似，总体数据均相对较小。因此，进水球阀折线关闭较直线关闭有利于减小抽水蓄能机组最大转速上升率。

由图11可知：尾水管最小绝对压力值在导叶关闭时间为40s时，不能满足尾水管最小绝对压力的控制要求。图中尾水管最小绝对压力的变化趋势与图7类似，但是尾水管最小绝对压力均相对较大，转速最大上升率均相对较小。因此，进水球阀折线关闭比直线关闭更有利于改善拒动机组的水力过渡过程。

在采用球阀先快后慢关闭规律的条件下，由导叶采用不同关闭时长直线关闭规律下的水力过渡计算结果可知：在导叶关闭时长为40s时，导叶正常关闭的甩负荷机组各调保参数均满足控制要求，且有较大裕度；对于导叶拒动的甩负荷机组，除40s直线关闭时，尾水管最小压力不能满足要求外，其余调保参数在各种直线关闭规律下都能满足控制要求。

5 结 语

结合一洞多机布置的抽水蓄能电站实例，有针对性地开展了机组导叶直线关闭时间和进水球阀关闭规律对抽水蓄能电站导叶关闭机组和拒动机组水力过渡过程的影响，得出了如下结论：

a.尾水管最小绝对压力随导叶关闭时间增加而上升，导叶关闭时间越长越能满足尾水管最小绝对压力的要求，转速最大上升率随导叶关闭时间增加而上升，但导叶关闭时间越长转速上升率越不能满足要求，因此为使抽水蓄能机组调保参数满足要求，选择合适的导叶关闭时长是必要的。

b.进水球阀采用折线关闭规律相比进水球阀采用传统的直线关闭规律，尾水管最小绝对压力增加，机组转速最大上升率降低。进水球阀折线关闭比传统直线关闭更有利于改善抽水蓄能机组的水力过渡过程。

c.通过对导叶拒动机组和导叶正常关闭机组的调保参数比较分析可知，机组导叶正常关闭时，调保参数更能满足控制要求。