基于多尺度模型的简支梁钢桥面铺装受力研究

宋君超，周艳，孟灵玥，李想

(1.济南黄河路桥建设集团有限公司，山东济南250014；2.山东建筑大学道路与交通工程山东省高校重点实验室，山东 济南250101；3.山东外事翻译职业学院国际商学院，山东 威海 264506；4.大华会计师事务所(特殊普通合伙)，北京100039)

0 引言

随着我国经济的迅速发展，大跨度钢桥的建设越来越多。正交异性钢桥面板广泛地应用于大跨度钢箱梁桥中，但其桥面铺装的早期损坏问题仍未解决[1-2]。目前，我国对各种桥型的正交异性钢桥面板的受力研究多采用局部简化模型[3-5]，对于各种不同的桥梁类型，如斜拉桥、悬索桥、刚构桥、连续梁桥、简支梁桥，均简化为一种模型—局部模型。采用局部模型法的研究者认为，正交异性板钢桥面铺装层的应力主要与钢桥面板的局部变形有关，跟桥梁整体受力关系不大，因此模型选取正交异性桥面板的局部。模型通常选取纵向3个横隔板的间距，一般不包含纵向腹板，有个别模型包含2道纵向腹板，横向包含6～14个U形肋，荷载只取一个双轮矩形均布荷载，其值为 0.7 MPa，作用范围为 0.6 m×0.2 m，桥面铺装的弹性模量大部分取1 000 MPa，所得应力和应变都比较小[3]，这显然不合理，以此作为指标设计的桥面铺装结构只能承受很小的应力和应变，而实际桥梁在自重、车辆荷载温度等共同作用下产生应力、应变是远大于模型分析结果的，因此导致桥面铺装产生病害。

多尺度模型见于大跨度钢箱梁桥的应力分析中[6-10]，采用此模型的学者并不多。多尺度模型多用于土木结构工程和桥梁工程力学计算中，极少用于桥面铺装的应力分析中[11-14]。此方法是将杆系模型与梁板壳模型相结合的一种有限元方法。杆系模型具有单元节点数量少、计算速度快、划分单元简单、计算机内存占用少等优点，但是这种方法不能够适应桥梁结构断面的复杂化，简化后的杆单元能够得到杆件的轴力、剪力和弯矩，但是对于应力只能得到大致整体值，比如根据截面惯性矩换算的截面上缘和下缘的整体应力，对于截面上各个具体的部件，比如桥面铺装层、横隔板、腹板等等具体的局部构件，是无法得到具体的应力分布的。而梁板壳实体模型能够克服杆系模型的缺点，可以得到桥梁任何部件的详细的应力分布，但是同时这种方法模型复杂，建模时间较长，计算机内存需求巨大，普通的计算机无法满足计算要求。因此在钢箱梁桥应力分析时，有些学者提出了用多尺度模型来计算钢箱梁的受力特性[6]。此方法将板壳单元与杆系单元相结合建立多尺度模型计算结构的受力特性，对研究相关部位及对结果感兴趣的构件用板壳单元模拟，其他部位用梁单元模型。苏庆田等[6-7]利用多尺度模型模拟了珠江黄埔大桥北汊桥和苏通大桥并分析了其受力特性，认为多尺度模型方法能够比较精确地计算和分析扁平钢箱梁板件的应力，能够更真实的反映各构件的受力情况。刘琦齐[15]建立斜拉桥多尺度模型并研究了其修正方法。

文章采用多尺度模型建立48 m跨径的简支梁桥的有限元模型，分析正交异性钢桥面铺装内最大应力、应变随钢桥面板厚度、横隔板间距、桥面铺装材料弹性模量、桥面铺装厚度的变化规律，从而对钢桥面铺装的设计和施工提供依据。

1 简支梁钢桥多尺度模型建立

1.1 多尺度模型理论

多尺度模型计算结构受力是在杆单元和板壳单元交界部位满足平截面假定基础上进行计算的。多尺度模型如图1所示，在板壳单元的交界面上有n个节点，位移参数为ui、vi、wi、θxi、θyi、θzi(节点i为1～10)。

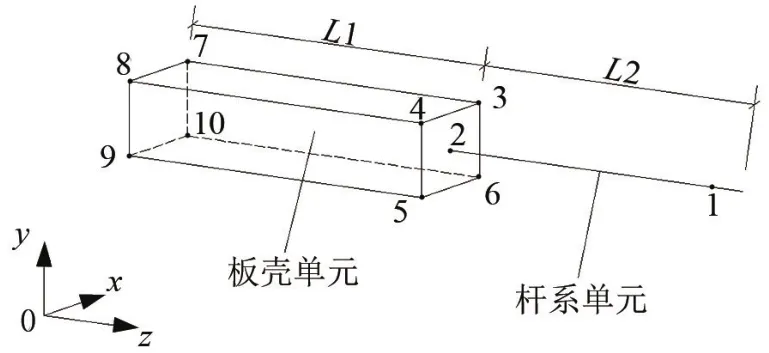
图1 多尺度模型示意图

为使交界面上位移协调，板壳单元的节点位移参数和杆件单元的节点位移参数之间并不各自独立，而是应存在一定的相关关系。板壳单元与杆件单元交界面上的节点刚体平动应是一致的，交界面上板壳单元i节点位移参数与杆件单元节点位移参数之间的约束方程由式(1)[16]表示为

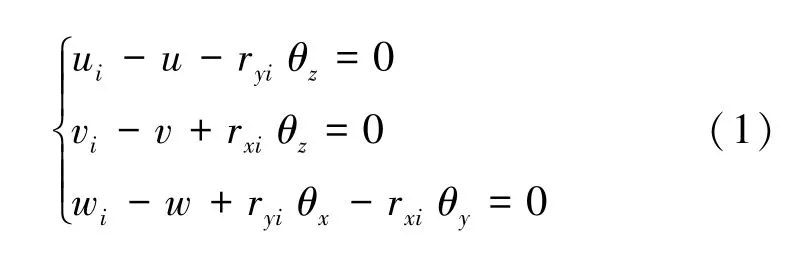
式中：u、v、w分别为节点 2 的位移；θx、θy、θz分别为节点 2 绕x、y、z轴转动角度；ui、vi、wi分别为交界界面上节点i的位移；rxi、ryi、rzi分别为板壳单元上节点i到节点2的距离在x、y、z轴上的投影距离。

1.2 多尺度模型试算—单梁模型

为验证多尺度模型的正确性，用单梁模型进行试算。分别建立具有完全相同材料和结构参数的简支梁整体壳模型和多尺度模型，并划分相同的网格密度，以便对计算结果进行分析比较。

算例模型为简支梁，其长为15 m、横截面高为1 m、宽为1 m；材料为16 Mn钢，材料特性包括弹性模量、泊松比、密度、热膨胀系数；2道横隔板位于5、20 m处；钢板厚度为0.01 m。

简支梁整体梁壳模型，结果截取5～10 m段，模型如图2所示。采用约束方程建立多尺度模型，模型如图3所示。模型中x、y、z向分别为横、竖、纵桥向。在杆系单元与壳单元界面建立约束方程，杆系单元部分采用自定义界面的梁单元，中间5～10 m段采用壳单元。

图2 整体模型图

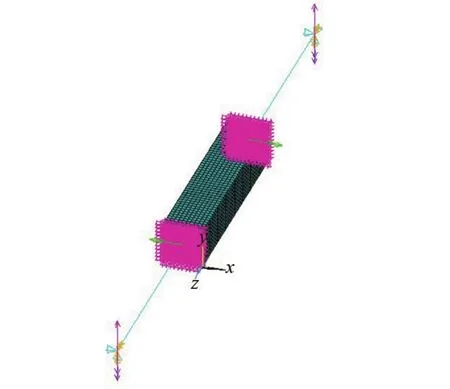
图3 约束方程多尺度模型图

分别对整体模型和多尺度单梁模型进行计算分析，得到的应力结果见表1。可以看出，2种模型的结果很接近。因此，约束方程法用于多尺度模型的计算分析是合适的。

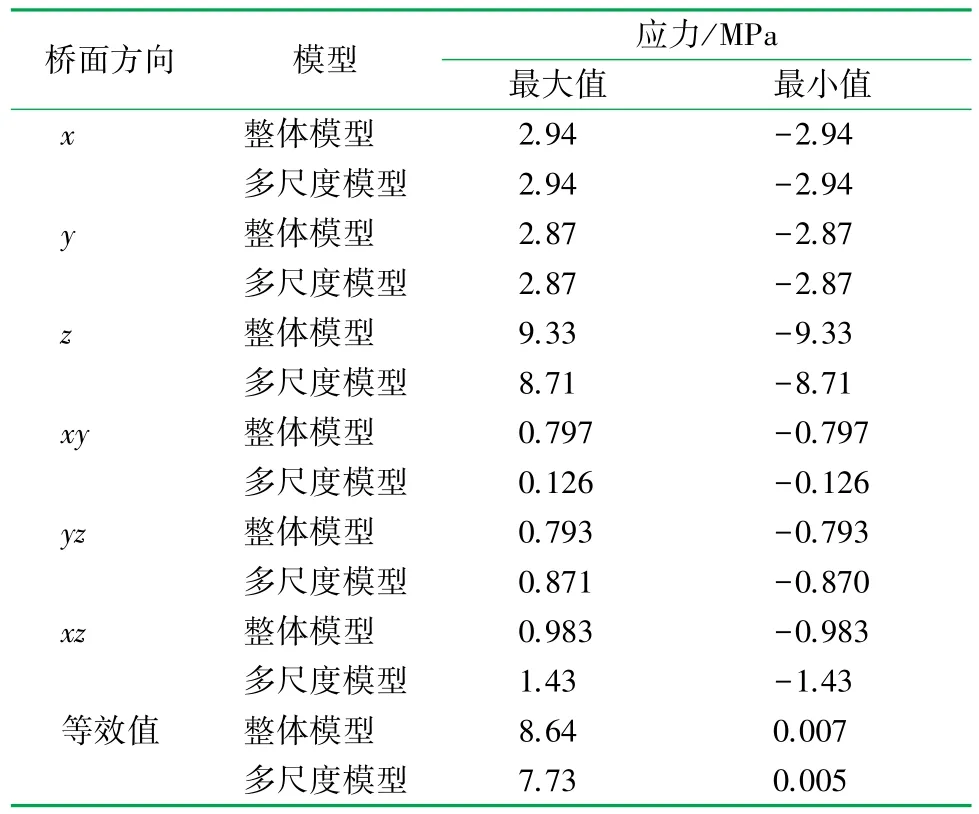
表1 2种单梁模型最大、最小应力结果表

1.3 多尺度模型建立

简支梁跨度为48 m，钢箱梁梁宽为22 m，梁高为2.1 m，单箱4室，5道腹板，腹板间距为4 m，腹板设有纵肋，U形肋只在顶板布置，底板以400 mm间距布置高度150 mm的纵肋，横隔板间隔为3 m，厚度为10 mm，中间留有人孔。采用ANSYS建立多尺度模型，桥面铺装采用SOLID45单元模拟，正交异性钢桥面板采用SHELL63单元模拟。为了模拟各种材料在各种温度下的弹性模量，桥面铺装厚度从0.1 m变化到0.01 m，桥面铺装层的弹性模量从300 MPa变化到 14 000 MPa，其中 500～14 000 MPa是以500 MPa间隔变化的，简支梁桥分别采用2种模型和参数进行计算，钢箱梁的参数见表2。

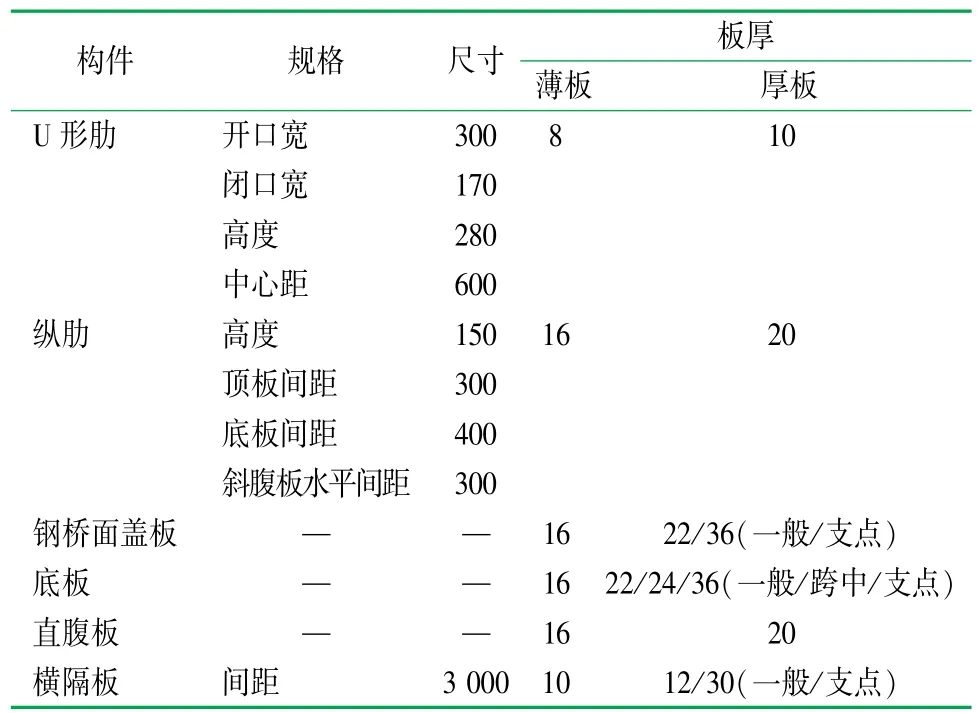
表2 简支梁桥钢箱梁参数表/mm

为满足计算精度及考虑计算速度，将荷载作用位置的单元尺寸细化为0.05，桥面铺装分成5层，竖向荷载用SURF154单元施加于铺装层顶面，水平荷载施加于桥面铺装之上，简支梁桥多尺度模型如图4所示。

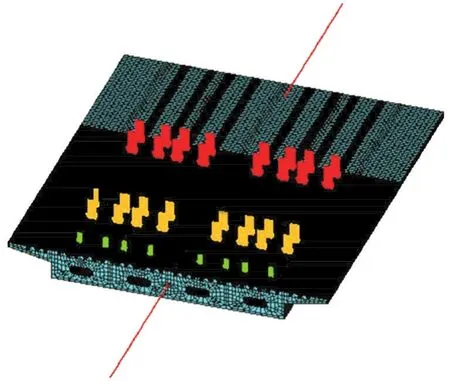
图4 简支梁桥多尺度模型图

2 基于多尺度模型的简支梁钢桥面铺装受力分析

2.1 横隔板间距及钢桥面板厚度对铺装层内最大应力、应变的影响

当桥面铺装厚度为0.1 m，铺装层材料弹性模量为300 MPa，不同板厚的钢箱梁应力与应变结果见表3。弹性模量为14 000 MPa，不同板厚及横隔梁间距为2 m桥面铺装的应力与应变结果见表4。

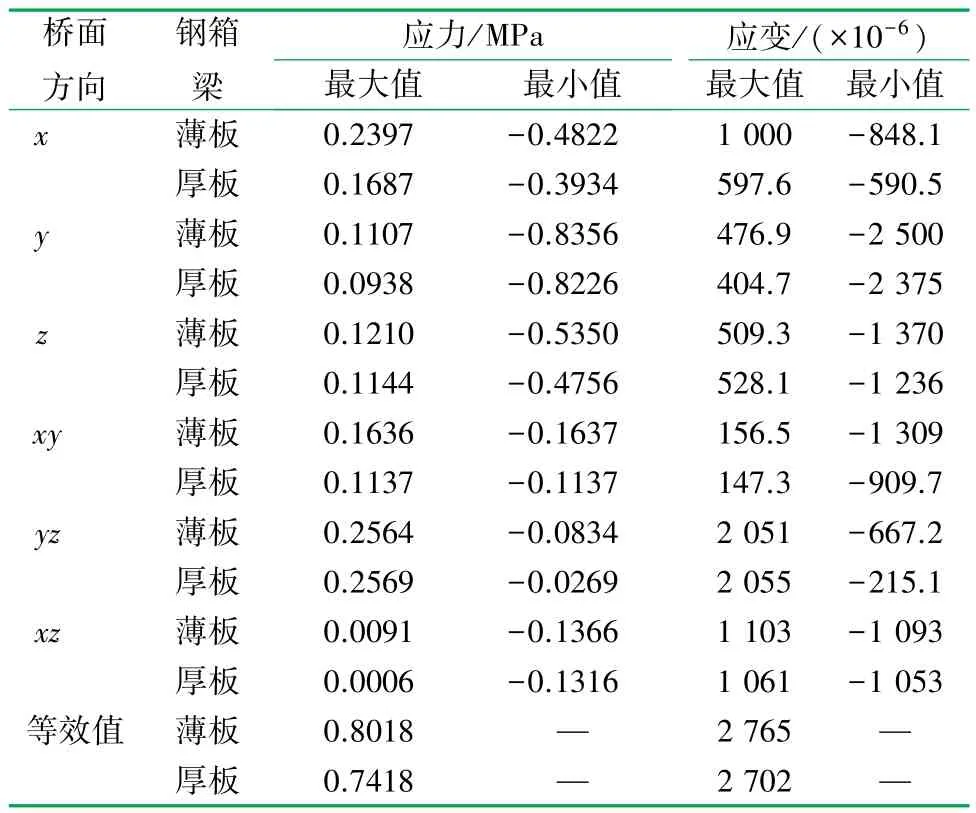
表3 铺装厚度0.1 m弹性模量300 MPa的不同板厚参数应力、应变表

当钢箱梁各板增厚时钢箱梁及桥面铺装各向最大应力应变均有所减小，但对于最小竖向压应变变化不大，最小竖向压应变主要与铺装层弹性模量和厚度有关系，弹性模量越小厚度越大，竖向压应变越大。板厚对纵向剪应变影响也不大，纵向剪应变受到水平力的影响较大。由此可见，钢箱梁板比较厚，结构设计比较合理，桥面铺装内各向最大应力和应变都会减小。横隔梁间距对结果影响不如板厚增加明显。

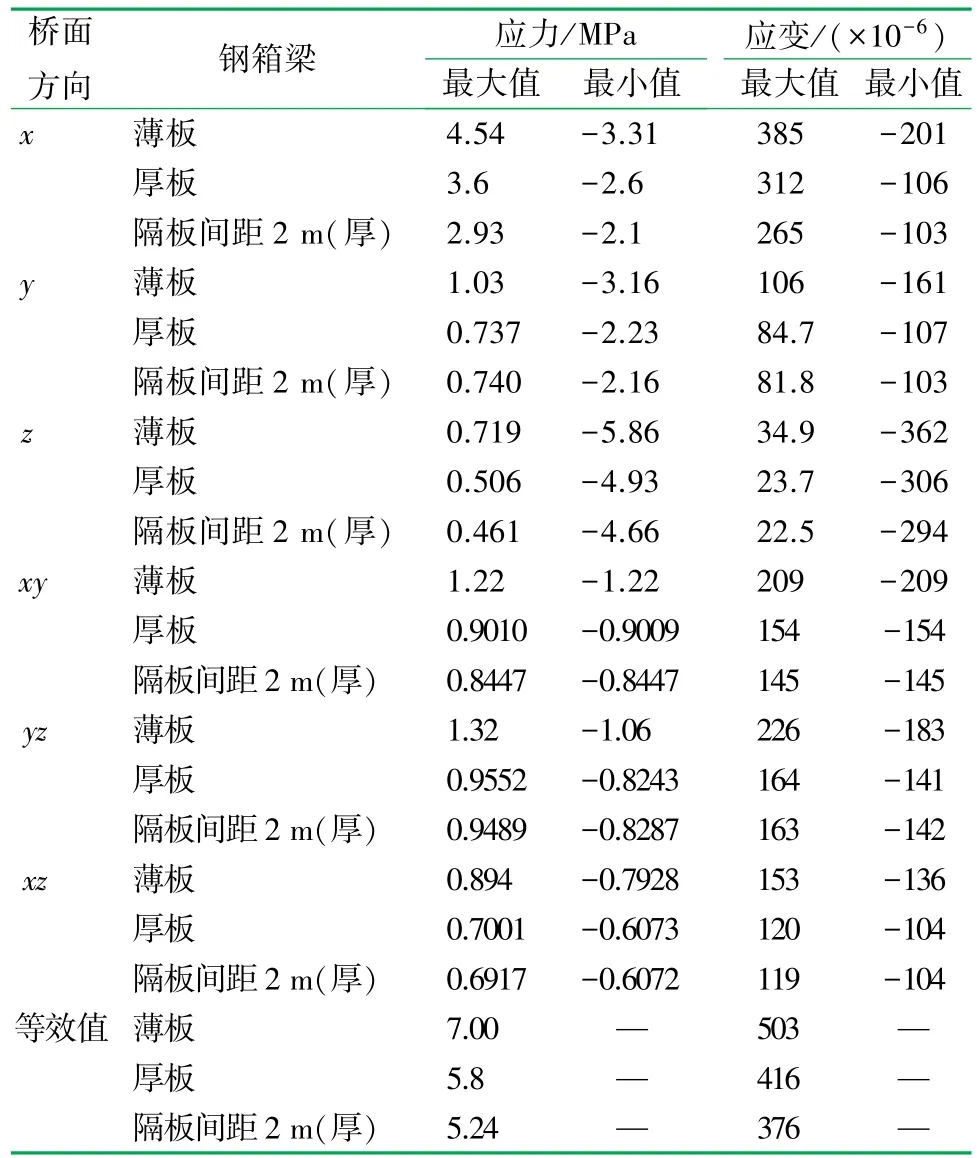
表4 弹性模量14 000 MPa不同板厚及横隔梁间距2 m的桥面铺装的应力、应变表

钢箱梁结构和板厚设计对桥面铺装的应力和应变影响较大，要想使桥面铺装具有较好的使用寿命，必须合理设计钢箱梁和正交异性钢桥面板。

2.2 材料弹性模量及厚度对铺装层内最大应力、应变的影响

考虑桥面铺装层厚度分别为0.1、0.07、0.05、0.03和0.01 m等5种厚度，常温桥面铺装材料抗压弹性模量在300～14 000 MPa情况下，简支梁桥和连续梁桥桥面铺装层内部各向应力和应变的结果，并绘制成曲线。

简支梁桥桥面铺装中横桥向最大拉应力和最大拉应变随弹性模量和铺装层厚度的变化情况如图5所示。x向最大拉应力随着弹性模量的增加而增加，而随着厚度的增加而减小，但厚度为0.01 m时，弹性模量和应力的增长呈线性关系。当回弹弹性模量＜1 000 MPa时，x向最大拉应变随厚度增加而增加，数值较大；当回弹弹性模量＞1 000 MPa时，应变随厚度增加而减小，数值趋于稳定，但厚度为0.03和0.01 m等2种情况的桥面铺装x向最大应变随弹性模量的变化不大。

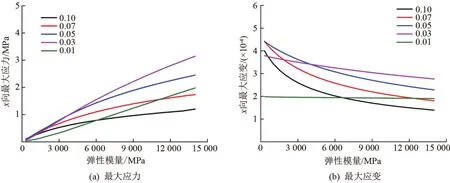
图5 x向最大应力和最大应变随弹性模量和厚度变化图

z向最大拉应力和最大拉应变随弹性模量和铺装层厚度的变化情况如图6所示。z向最大拉应力随着回弹弹性模量的增加而增大，而随着厚度的增加而增大，当厚度＞0.01 m，在回弹弹性模量＜1 500 MPa时，z向最大拉应力随回弹弹性模量增大而稍有减小。z向最大拉应变随回弹弹性模量的减小而迅速减小，回弹弹性模量＞1 000 MPa后，弹性模量变化极微小，微应变平稳保持在＜20。

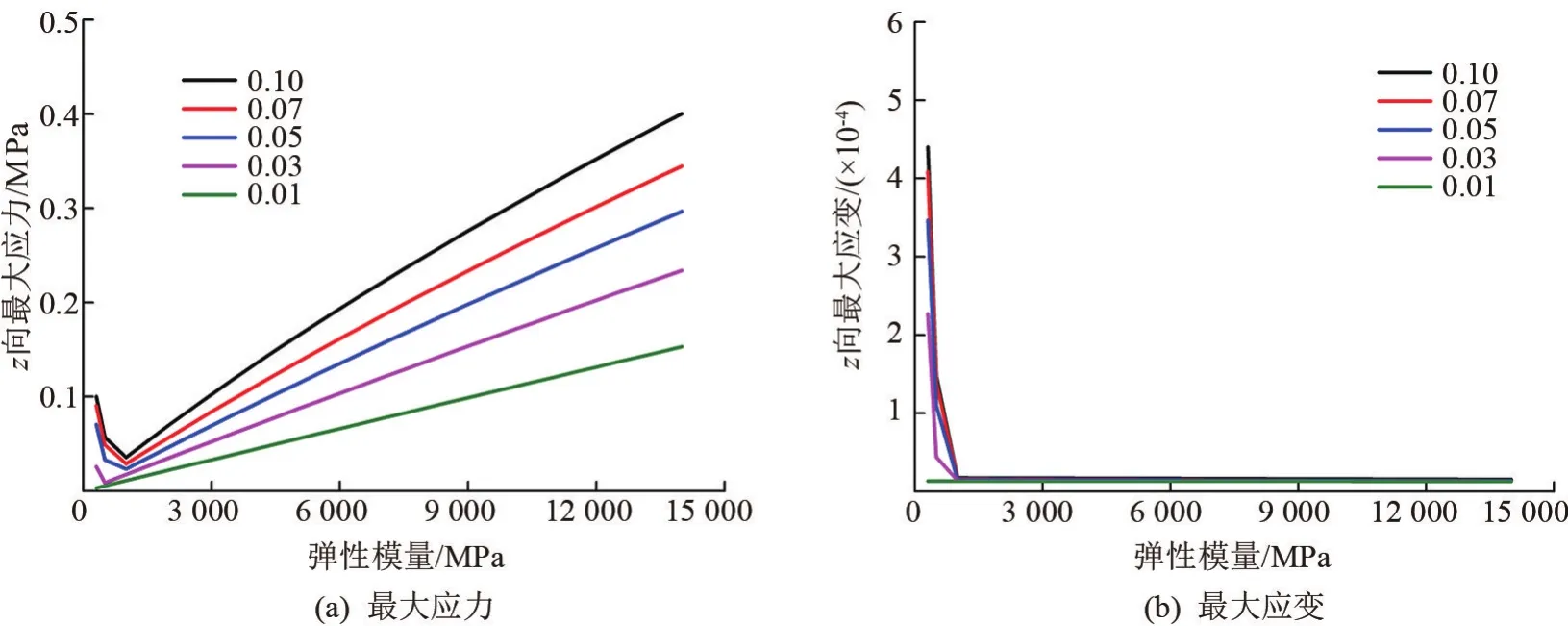
图6 z向最大拉应力和最大拉应变随弹性模量和厚度变化图

yz向最大负剪应力和最大负剪应变随弹性模量和铺装层厚度的变化情况如图7所示。yz向最大负剪应力随弹性模量和厚度的增加而增加，当最大负剪应变弹性模量＞2 000 MPa时，随弹性模量和厚度的增加而减小。通过模型分析各向最大应力、应变均有相似结果：最大应力一般随弹性模量增加而增加，最大应变一般随弹性模量增加而减小，当弹性模量＜1 500 MPa时，各向应变急剧增加。

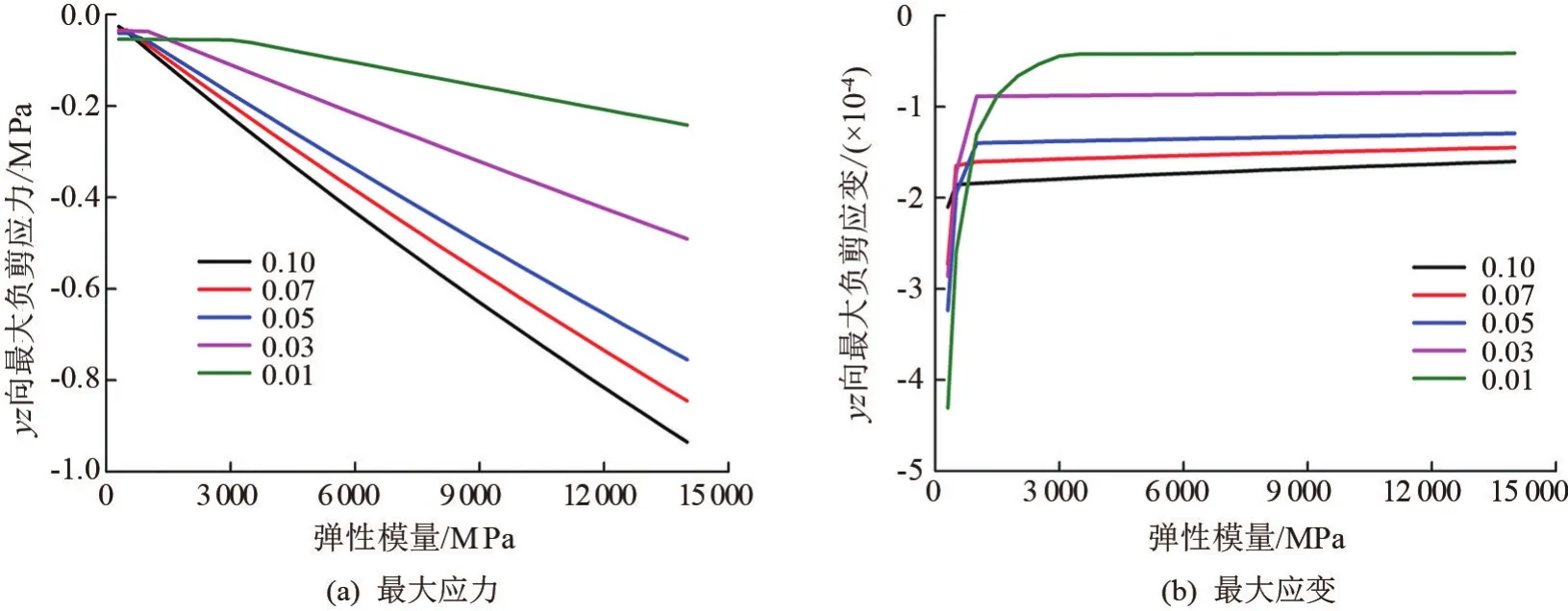
图7 yz向最大剪应力和最大剪应变随弹性模量和厚度变化图

3 结论

利用建立的简支梁桥多尺度模型，通过对简支梁桥正交异性钢桥面板桥面铺装层内各向最大应力、应变随钢桥面板的厚度、横隔板间距、桥面铺装厚度、桥面铺装材料弹性模量变化的规律研究，主要得到以下结论：

(1)当钢箱梁各板增厚时钢箱梁及桥面铺装各向最大应力应变均有所减小，随正交异性钢桥面板板厚增加，钢箱梁和桥面铺装内应力应变减小较多，横隔板间距减小对应力、应变影响不大。

(2)简支梁钢桥面铺装内应力、应变随铺装材料弹性模量和铺装层厚度变化有着相似的规律：应力一般随弹性模量增加而增加，应变随弹性模量增加而减小，弹性模量＜1 500 MPa会使各向应变急剧增加；在钢桥面铺装的设计中，在夏季高温情况下，要避免使用弹性模量＜1 500 MPa的材料作为钢桥面的铺装材料。

(3)对简支梁桥，增加桥面板厚度、优化钢箱梁的尺寸能够有效减小钢桥面铺装的各向受力。