光学测量方法在手机跌落测试中的应用

徐劲澜　梁晋　赵鹏亮　张桁维　孟繁昌

摘要：手机跌落试验主要用于检验手机质量，有限元分析模拟仿真方法能够帮助厂家在产品开发阶段优化手机结构，但不能对成品实物进行质量检验。针对上述间题，该文提出一种基于光学测量的手机跌落试验方法，采用双目立体视觉原理，利用摄影测量技术，提高数字图像相关法匹配精度，使用高速相机对手机跌落过程进行连续采集，提高系统标定精度后通过图像数据计算分析获取手机跌落过程中的全场位移及应变值。该文用华为荣耀4A手机前壳进行试验，成功获取其跌落过程中的三维全场变形数据，证明基于数字图像相关法手机跌落试验方法具有高精度、试验过程简便等优点，满足成品手机质量检测的需求。

关键词：光学测量;手机跌落试验;数字图像相关;全场应变

中图分类号：TP391 文献标志码：A 文章编号：1674-5124（2019）01-0034-06

0 引言

手机跌落试验是用于检验手机质量的标准试验，目前国内外均采用有限元分析模拟仿真的方法模拟手机跌落试验，即先用CAD三维建模软件建立手机模型，用ANSYS软件对模型进行前处理，最后使用如LS-DYNA一类的动态仿真软件完成仿真模拟试验，从而获取手机跌落碰撞过程中的应力云图、应变云图等数据[1-2]。这种方法广泛应用于产品开发阶段对产品手机进行结构耐撞性的分析，从而优化手机结构，提高产品的可靠性，降低产品开发成本，提高产品的市场竞争能力。由于基于ANSYS软件的手机跌落试验使用软件建模模型进行试验，其建模根据试验侧重点有一定简化，故所得模拟仿真结果与实际手机碰撞结果仍有一定区别，故其方法虽然对结构的设计与改善有一定指导作用，但无法更加精确地完成成品手机质量的检验，为了准确检验手机的质量，还需要对实物手机进行手机跌落试验。

现如今对于手机跌落碰撞试验三维全场应力应变的测量，传统检测设备由于其接触性、鲁棒性、单点检测、实验设备复杂等因素，无法满足全场力学性能检测[3]，而在材料力学性能测试领域得到广泛应用的数字图像相关法（DIC），由于其非接触、高精度、全场测量、实验设备简单等优点[4]能够满足手机质量检验的需求。本文提出基于数字图像相关法的光学测量方法完成手机跌落试验，采用一种非参数化的畸变校正方法提高系统标定精度，并在亚像素差值过程中选用三次B样条提高匹配精度，实现手机跌落试验的精确测量。

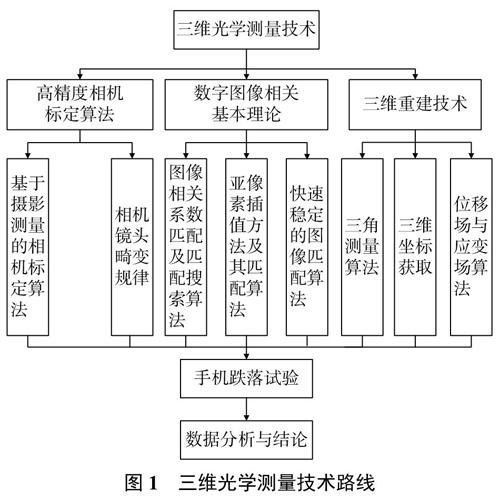
1 三维光学测量技术

三维光学测量技术即使用双目立体视觉原理，通过标定CCD相机采集图像，利用数字图像相关技术对采集得到的图像进行后处理计算获取被测目标三维位移场与应变场的方法，主要包含双目立体视觉、相机标定技术、数字图像相关匹配技术、三维重建技术、应变场计算。其过程主要为根据摄影测量学原理计算摄像机系统的内外参数[5]、利用数值图像相关法对左右相机以及被测物件变形前后的图像进行匹配[6-8]、利用标定获得的参数对匹配点进行三维重建获得目标点的三维坐标[9-10]、通过三维坐标计算目标点的位移场与应变场[11]，其技术路线如图1所示。

对于变形及应变测量，三维光学测量方法以其非接触、全场测量，得到了广泛的应用。随着相关学科理论的不断发展，和各种新硬件、新设备的出现，三位光学测量技术的发展也向着更精确、更快速、更稳定发展，目前三维重建技术已发展成熟，而高精度相机的标定算法与数字图像相关匹配算法的精度仍然有大量提升的空间。

2 非参数化畸变模型

在光学系统中，成像过程通常用针孔模型描述，考虑到透镜本身加工误差和装配误差的存在，使得透镜像差（例如球差、慧差、像面弯曲和畸变等）的存在不可避免，这就使得物体点的真实成像位置偏离原始的投影位置，在图像上产生枕形畸变、桶形畸变、线性畸变等成像误差。本文首先不考虑光学畸变误差，直接采用标定板基于理想的透视投影模型标定显微光学系统;然后，根據标定结果求解标定板上所有标志点的重投影误差;最后，利用曲面拟合重投影误差，从而建立显微成像的畸变校正场。

根据CCD相机成像视场中间位置畸变几乎为零的特点，本文认为视场中间区域为无畸变的理想区域，如图2所示，在此区域中获取特征点的成像坐标，求得其任意X方向与Y方向的图像坐标间隔x、y，再对应于其在标定板中的物理间隔，求得X、Y方向投影间隔的比例因子S_x、S_y，由此解算出标定板中所有特征点的图像坐标，而后与特征点畸变成像坐标做差，获得所有特征点所在视场位置的畸变值，进而拟合出整个视场畸变场，流程如图3所示。

将标定图像根据上述方法校正畸变后，根据课题组所提出的外参数求解方法[12]，可以获得系统的外参数，即两相机坐标转换关系的旋转矩阵R与平移矩阵T，其关系如下：

其中[x_ly_lz_l]^T表示左相机的坐标系，[x_ry_rz_r]^T表示右相机的坐标系。

3 B样条亚像素灰度插值

数字图像相关匹配技术是测量系统中误差最大来源，因此提高数字图像相关匹配的精度具有重大意义。数字图像相关匹配过程中包含了整像素搜索与亚像素搜索，整像素搜索后的匹配精度较低，为了提高匹配精度，对图像整像素进行亚像素插值，再以整像素搜索结果作为初值进行亚像素匹配。在亚像素插值函数的选取中，复杂的插值函数具有较高的精度但计算效率低，简单的插值函计算效率高但精度不低，因此本文针对不同插值函数对匹配结果的精度及计算效率进行了研究，在保证足够高的精度与计算效率的情况下，选择三次B样条函数进行亚像素插值。

常用的亚像素插值方法是双线性插值方法，其计算量小，然而精度较低，无法满足高精度测量的需求。而B样条具有可微性、凸包性、变差减少性、磨光性、几何不变性与放射不变性，其样条更加光滑，且样条中的点仅受相邻几个控制点的影响，与其他顶点无关，因而可以减少累计误差。B样条函数可以表示为

其中d_m为控制点系数，N_n，k（x）为基函数，而基函数具有递归型，对其描述为

其中，k表示B样条的幂次，t为节点，下标i为B样条的序号。二维的B样条曲面表示为

其中，n_i=m_i-p-1，n_j=m_j-p-1，m_i+1和m_j+1分别是x和y方向的样条节点数，p为B样条的次数，α_i，j，β_i，j为样条曲面的（n_i+1）×（n_i+1）个样条系数，N_i，p（x）和N_j，p（x）分别为样条曲面的x和y方向的基础函数。

4 实验与分析

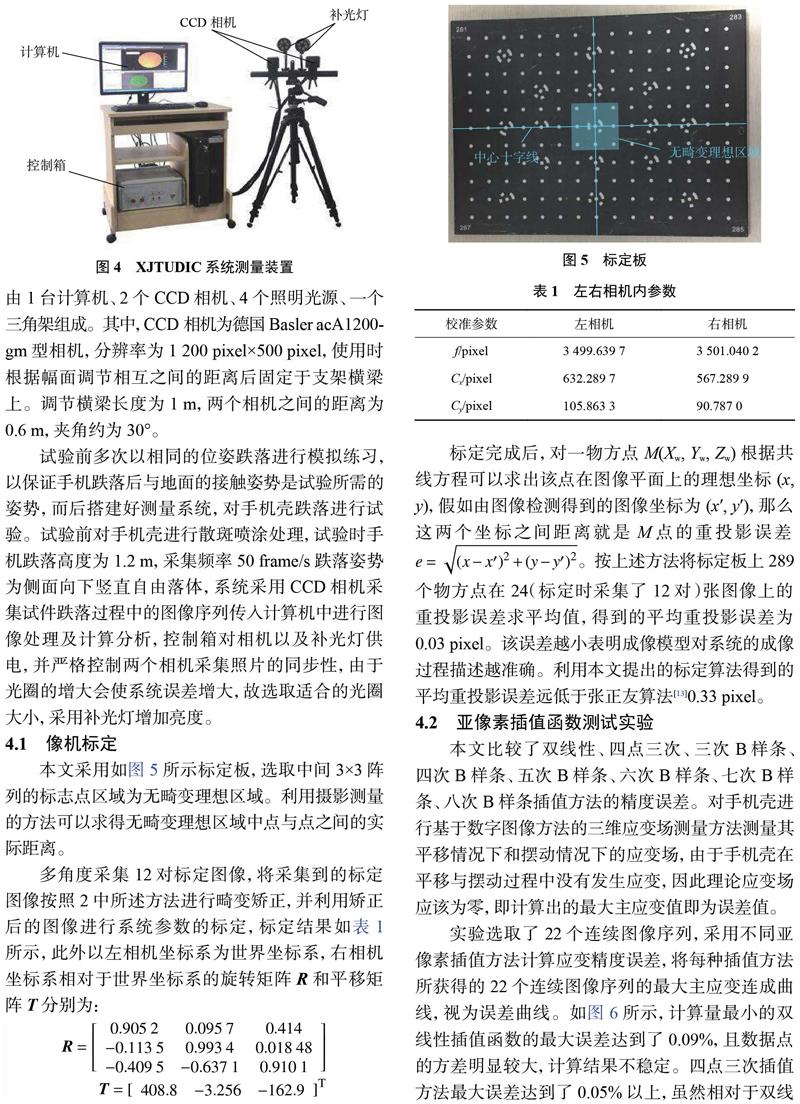
本文采用的三维测量系统为XJTUDIC三维散斑数字图像相关测量系统。如图4所示，测量系统由1台计算机、2个CCD相机、4个照明光源、一个三角架组成。其中，CCD相机为德国Basler acA1200-gm型相机，分辨率为1200pixel×500pixel，使用时根据幅面调节相互之间的距离后固定于支架横梁上。调节横梁长度为1m，两个相机之间的距离为0.6m，夹角约为30°。

试验前多次以相同的位姿跌落进行模拟练习，以保证手机跌落后与地面的接触姿势是试验所需的姿势，而后搭建好测量系统，对手机壳跌落进行试验。试验前对手机壳进行散斑喷涂处理，试验时手机跌落高度为1.2m，采集频率50frame/s跌落姿势为侧面向下竖直自由落体，系统采用CCD相机采集试件跌落过程中的图像序列传人计算机中进行图像处理及计算分析，控制箱对相机以及补光灯供电，并严格控制两个相机采集照片的同步性，由于光圈的增大会使系统误差增大，故选取适合的光圈大小，采用补光灯增加亮度。

4.1 像机标定

本文采用如图5所示标定板，选取中间3X3阵列的标志点区域为无畸变理想区域。利用摄影测量的方法可以求得无畸变理想区域中点与点之间的实际距离。

多角度采集12对标定图像，将采集到的标定图像按照2中所述方法进行畸变矫正，并利用矫正后的图像进行系统参数的标定，标定结果如表1所示，此外以左相机坐标系为世界坐标系，右相机坐标系相对于世界坐标系的旋转矩阵R和平移矩阵T分别为：

T=[408.8 -3.256 -162.9]^T

标定完成后，对一物方点M（X_W，Y_W，Z_W）根据共线方程可以求出该点在图像平面上的理想坐标（x，y），假如由图像检测得到的图像坐标为（x'，y'）敲？这两个坐标之间距离就是M点的重投影误差。按上述方法将标定板上289个物方点在24（标定时采集了12对）张图像上的重投影误差求平均值，得到的平均重投影误差为0.03pixel。该误差越小表明成像模型对系统的成像过程描述越准确。利用本文提出的标定算法得到的平均重投影误差远低于张正友算法[13]0.33pixel。

4.2 亚像素插值函数测试实验

本文比较了双线性、四点三次、三次B样条、四次B样条、五次B样条、六次B样条、七次B样条、八次B样条插值方法的精度误差。对手机壳进行基于数字图像方法的三维应变场测量方法测量其平移情况下和摆动情况下的应变场，由于手机壳在平移与摆动过程中没有发生应变，因此理论应变场应该为零，即计算出的最大主应变值即为误差值。

实验选取了22个连续图像序列，采用不同亚像素插值方法计算应变精度误差，将每种插值方法所获得的22个连续图像序列的最大主应变连成曲线，视为误差曲线。如图6所示，计算量最小的双线性插值函数的最大误差达到了0.09%，且数据点的方差明显较大，计算结果不稳定。四点三次插值方法最大误差达到了0.05%以上，虽然相对于双线性插值较为稳定，但其稳定性任然不如B样条插值方法。在B样条插值方法中，三次B样条最大误差值接近0.048%，仅比高阶B样条插值方法高出0.006%，且稳定性较高阶B样条插值方法仅略有不足，因此三次B样条插值方法与高阶B样条插值方法所获得的精度差距不大，同时考虑到随着B样条函数阶次的增加，其计算量的快速增大，综合考虑精度与计算效率两个因素以后，选取三次B样条作为插值函数完成亚像素插值。

4.3 手机跌落测试实验

实验所用手机为华为荣耀4A，测试部分为手机前壳，碰撞过程中手机前壳的左下方部分首先接触地面，而后左下方部分弹起的同时右下方部分接触地面，最后左下方部分接触地面，右下方部分弹起。

表面位移场与应变场测量区域为图7中绿色网格区域，其碰撞过程中某时刻的表面最大主应力分布如图8所示，最大主应变最大点的应变值为1.1302%，靠近碰撞接触边缘，与理论应变最大区域相符合。整个测试过程中单点（选取图7中红色方框中心点）应变随时间变化趋势如图9所示，初始时刻最大主应变为0，随着手机开始跌落，在跌落过程中产生了一定的倾斜，因而最大主应力略有一定变化，但在约第18状态时，最大主应变值从。左右明显至约1.1%，此时为手机壳右下方部分接触地面，而后由于左下方部分持续接触地面，应變值缓慢持续上升。

此方法不仅可以获取材料变形过程中X、Y、Z3个方向的位移场与应变场，还可以测得各个方向位移与应变的方向向量等所有相关的物理量。本实验仅选择应变场中任意两点之间的距离和应变场中任意一点的最大主应变值随时间的变化做分析。

任意选择如图10所示两点（红色方框中心点）之间的距离，对其描绘如图11所示曲线，点距在初始状态下为约62.4mm，落地前在误差范围内跳动，在第10个状态后骤降至约61.5mm，有明显约1mm的减少，即为压缩状态，说明此时手机前壳第1次与地面接触（如图10所示）。点距在第16个状态时回复并有一定上升至约62.7mm，为第1次碰撞后离开地面的状态，同时其比较初始状态62.4mm有一定的拉伸量，这个现象是由于材料的弹性，致使材料从压缩状态恢复后继续变形，在约第22个状态的时候拉伸变形至最大，而后继续反向变形，即从拉伸状态变形为压缩状态，若没有第2次碰撞，变形将以一种逐渐减小的拉伸一压缩震荡的方式恢复原有的点距。

5 结束语

本文针对跌落碰撞试验中的成品手机质量检测提出了一种能够检测其位移场与应变场的光学测量方法，其主要内容为：

1）针对传统10参数标定方法计算效率低和存在局限性等缺点，提出了一种新的畸变校正方法，简化了系统标定计算过程，保证了系统的高精度。

2）对数字图像相关法中亚像素插值函数的选取做出了相关研究，结果表明，在同时对精度和计算效率做出要求得情况下，选择三次B样条作为插值函数较为恰当。

3）采用光学测量方法对华为荣耀4A手机前壳进行了试验，成功获取了其表面的三维全场位移以及应变，同时还对单点以及两点之间的距离随时间变化进行了曲线分析。

参考文献

[1]LAI Y S，YANG P C，YEH C L.Effects of different drop testconditions on board-level reliability of chip-scalepackages[J].Microelectronics Reliability，2007，48（2）：274-281.

[2]陈飞，岳应娟，杜小军，等.基于LS-DYNA的高压气瓶跌落仿真分析[J].武汉科技大学学报，2013，36（2）：146-149.

[3]WANG Y Y，LU C，LEI Jet al.Simulation of drop/impactreliability for electronic devices[J].Finite Elements inAnalysis and Design，2005，41：667-680.

[4]SUTTON M A，MCNEIL S R，HELM J D，et al.Advances intwo-dimensional and three-dimensional computer vision[J].Topics in Applied Physics，Springer Verlag，2000，77：323-372.

[5]ZHANG Z Y.A flexible new technique for cameracalibration[J].IEEE Transactions on Pattern AnalysisMachine Intelligence，2000，22（11）：1300-1334.

[6]唐正宗，梁晋，肖振中，等.大变形测量数字图像的种子点匹配方法[J].西安交通大学学报，2010，44（11）：51-55.

[7]PAN B，XIE H，WANG Z.Equivalence of digital imagecorrelation criteria for pattern matching[J].Applied Optics，2010，49（28）：5501-5509.

[8]HARTLEY R I，STURM P.Triangulation[J].ComputerVision and Image Understanding，1997，68（2）：146-157.

[9]URK A O，ALICI U H，ULUSOY I，et al.Three-dimensionalface reconstruction using stereo images and structured light[C]//IEEE 16th Signal Processing，Communication andApplications Conference.IEEE，2008.

[10]CUI H N，SHEN S H，HU Z Y.Global fusion of generalizedcamera model for efficient large-scale structure frommotion[J].Science China Information Sciences，2017，60（3）：038101：1-038101：3.

[11]PAN B，XIE H M.Full-strain field measurement based onleast-square fitting of local displacement for digital imagecorrelation method[J].Acta Optica Sinica，2007，27（11）：1980-1986.

[12]龔春园，梁晋，温广瑞，等.投影仪全参数平面线性估计得高精度标定方法[J].西安交通大学学报，2016，50（11）：36-42.[13]PAN B，ASUNDI A，XIE H，et al.Digital image correlationusing iterative least squares and pointwise least squares fordisplacement field and strain field measurements[J].Opticsand Lasers in Engineering，2009，47（7/8）：865-874.