一种考虑复杂孔隙结构的泥页岩地震岩石物理模型

王 团, 赵海波, 李奎周, 甘立灯, 霍秋立

(1.大庆油田有限责任公司勘探开发研究院,黑龙江大庆 163712; 2.中国石油勘探开发研究院,北京 100083)

对于泥页岩油勘探而言,地震技术是储层识别和评价的核心,泥页岩的地震岩石物理是利用地震属性预测储层属性特征及其力学特征的桥梁[1-4]。国外在泥页岩勘探方面起步较早,对于泥页岩储层岩石物理研究较为系统。针对北美黑色Bakken页岩,Vernik等[5-6]基于Backus平均理论进行岩石物理建模,系统研究了有机质体积分数、成熟度等因素对页岩各向异性的影响。Sayers[7]通过建立岩石物理模型,研究了黏土矿物的分布对页岩弹性参数的影响。Nicols-López和Valdiviezo-Mijangos[8]基于自洽方程,综合考虑页岩岩石骨架的矿物组分、有机质和孔隙流体的影响,建立了页岩岩石物理模板,指导了页岩储层评价。国内方面,关于泥页岩岩石物理及应用研究近些年逐步得到重视。张广智等[9]基于页岩岩石物理等效模型,实现了最小水平地应力的有效预测。邓继新等[10]基于龙马溪组页岩微观结构特征分析,建立相应的地震岩石物理表征模型,为页岩气储层“甜点”预测提供了依据。由于不同地区泥页岩储层在沉积环境和成岩作用(矿物组分、沉积结构、孔隙类型等)等方面存在差异,造成针对特定储层的岩石物理研究结果也具有区域性而不能随意外推。国内泥页岩勘探主要集中在四川盆地龙马溪组等区域,对于古龙凹陷青山口组复杂陆相泥页岩油储层,目前还没有针对性的岩石物理建模理论,因此建立适用于该地区泥页岩油地震岩石物理模型并分析其岩石物理规律具有重要的意义。笔者从研究区泥页岩地质特征分析出发,以岩石物理基础理论为依据,提出适用于富有机质泥页岩的复杂孔隙结构岩石物理模型,基于模型分析有机质体积分数、裂缝孔隙度和孔隙纵横比等因素对岩石弹性性质的影响,并根据有机质体积分数和孔隙度的影响建立岩石物理交会模板,进行泥页岩储层的纵、横波速度预测。

1 泥页岩基本地质特征

1.1 岩石学特征

通过对松辽盆地北部青山口组67个泥页岩岩心样品X射线衍射全岩分析可知,储层岩石骨架的矿物组分主要包括黏土矿物、石英、长石、方解石和白云石,其中石英体积分数平均为36%,长石体积分数平均为21%,碳酸盐矿物体积分数平均为7%,黏土矿物体积分数平均为36%,黏土矿物以伊利石为主,占60%～80%。

通过与北美沃斯堡盆地Barnett页岩[11]相比(图1),青山口组泥页岩长石含量高,碳酸盐含量低,石英和黏土含量大致相当。但Barnett页岩富含硅质泥岩和含钙泥岩,高有机碳丰度烃源岩主要发育在硅质泥岩中,而青山口组泥岩以黏土质泥岩为主,少量含钙泥岩,泥岩中的硅以碎屑搬运沉积为主,缺少过剩硅,脆性一般。因此Barnett页岩与青山口组泥页岩岩相学特征虽然较相似,但岩石特征和矿物组分具有一定的差异性。

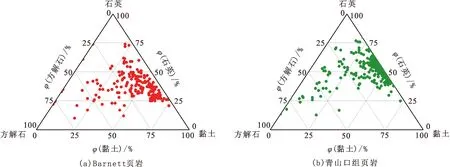
图1 岩心样品矿物组分三角图Fig.1 Temary plot of sample mineral composition

1.2 微观结构特征

根据扫描电镜、铸体薄片和岩心样品观察结果可知,青山口组陆相泥页岩储层的孔隙空间主要包括微观孔隙和裂缝系统两大部分。

微观孔隙主要为原生粒间孔、次生溶蚀孔、晶间微孔、生物铸模孔和有机质孔,原生粒间孔(图2(a))主要存在于脆性矿物颗粒或晶粒之间以及脆性矿物颗粒与黏土之间,孔径在1～5 μm;次生溶蚀孔(图2(b))多为胶结物溶解而形成,孔径相对较大,主要分布在2～10 μm;晶间微孔主要指黏土矿物晶间微孔(图2(c))和石英颗粒晶间微孔(图2(d)),微孔隙很细小,一般小于1 μm;生物铸模孔(图2(e))主要为介形虫骨架和腔体内部溶解发育孔隙,孔径可达100 μm,呈孤立椭球状;有机质孔主要指的是有机质收缩孔(图2(f)),为藻类生烃后残留孔隙,呈不规则状,多为纳米孔。其中原生粒间孔和次生溶蚀孔连通性较好,晶间微孔、生物铸模孔和有机质孔的连通性较差,多呈孤立状存在。裂缝系统则主要包括构造裂缝、成岩裂缝和层间缝,以构造裂缝为主,裂缝倾角普遍大于70°,发育少量的斜交缝和低角度裂缝,利用蒙特卡洛逼近法对岩心裂缝物性进行计算,裂缝孔隙度一般小于0.35%,最大为0.65%,渗透率主要分布在(25～100)×10-3μm2,说明裂缝是泥页岩油的重要储集空间和主要渗流通道。

有机质是泥页岩油聚集成藏最重要的控制因素之一,根据扫描电镜照片(图2(g))观察可知,泥质是泥页岩中的主要基质矿物,有机质呈块状在其中分布,有机质中孔隙不发育,总有机碳含量(TOC)平均大于2%,镜质体反射率在0.9%～1.7%,处于成熟—高成熟生油阶段。这种特征与美国威利斯顿盆地Bakken页岩[12]和四川盆地龙马溪组页岩[13-14]存在明显差异,Bakken页岩中有机质呈近似平行层理的条带状分布,龙马溪组页岩中有机质主要呈分散状分布,局部呈条带状,其内部普遍发育有机质微孔隙,镜质体反射率为2.5%～3.2%,处于高—过成熟生气阶段。

图2 微观孔隙和有机质的扫描电镜及铸体薄片照片Fig.2 SEM photomicrographs and casting thin sections of micro-porosity and organic

2 泥页岩地震岩石物理模型

通过上述对松辽盆地北部青山口组陆相泥页岩基本地质特征进行分析,发现其岩石结构比较复杂,与国内外其他盆地泥页岩存在明显差异,主要表现在岩石骨架矿物组分、孔隙结构、有机质的分布特征等方面,为此针对松辽盆地北部青山口组特殊的泥页岩油沉积和成岩特点,综合利用Kuster & Toksöz模型、自相容模型、双连通孔隙模型和线性滑动模型,建立一种适用于松辽盆地青山口组的复杂孔隙结构泥页岩地震岩石物理模型。构建流程主要分为岩石基质等效弹性模量的计算、“干”孔隙岩石骨架弹性模量的求取以及饱和岩石弹性参数的计算3部分。其流程如图3所示。

2.1 岩石基质等效弹性模量的计算

利用V-R-H平均混合石英、长石、方解石和白云石,得到混合矿物1;将有机质作为球型包含物,利用Kuster & Toksöz模型添加到泥质背景中,得到混合矿物2;使用自洽模型将这两种等效介质进行混合,得到岩石基质的等效弹性模量。

2.1.1 Voigt-Reuss-Hill平均

V-R-H平均[15]可以用来计算各向同性、完全弹性介质的等效弹性模量,在古龙凹陷青山口组泥页岩储层岩石骨架矿物组分中,石英、长石、方解石和白云石均为刚性介质,弹性性质较为接近,可用该模型进行混合,其表达式为

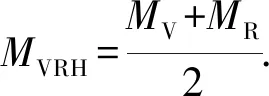
(1)

其中

式中,φi和Mi分别为第i种组分的体积分数和弹性模量;MVRH为混合矿物的弹性模量。

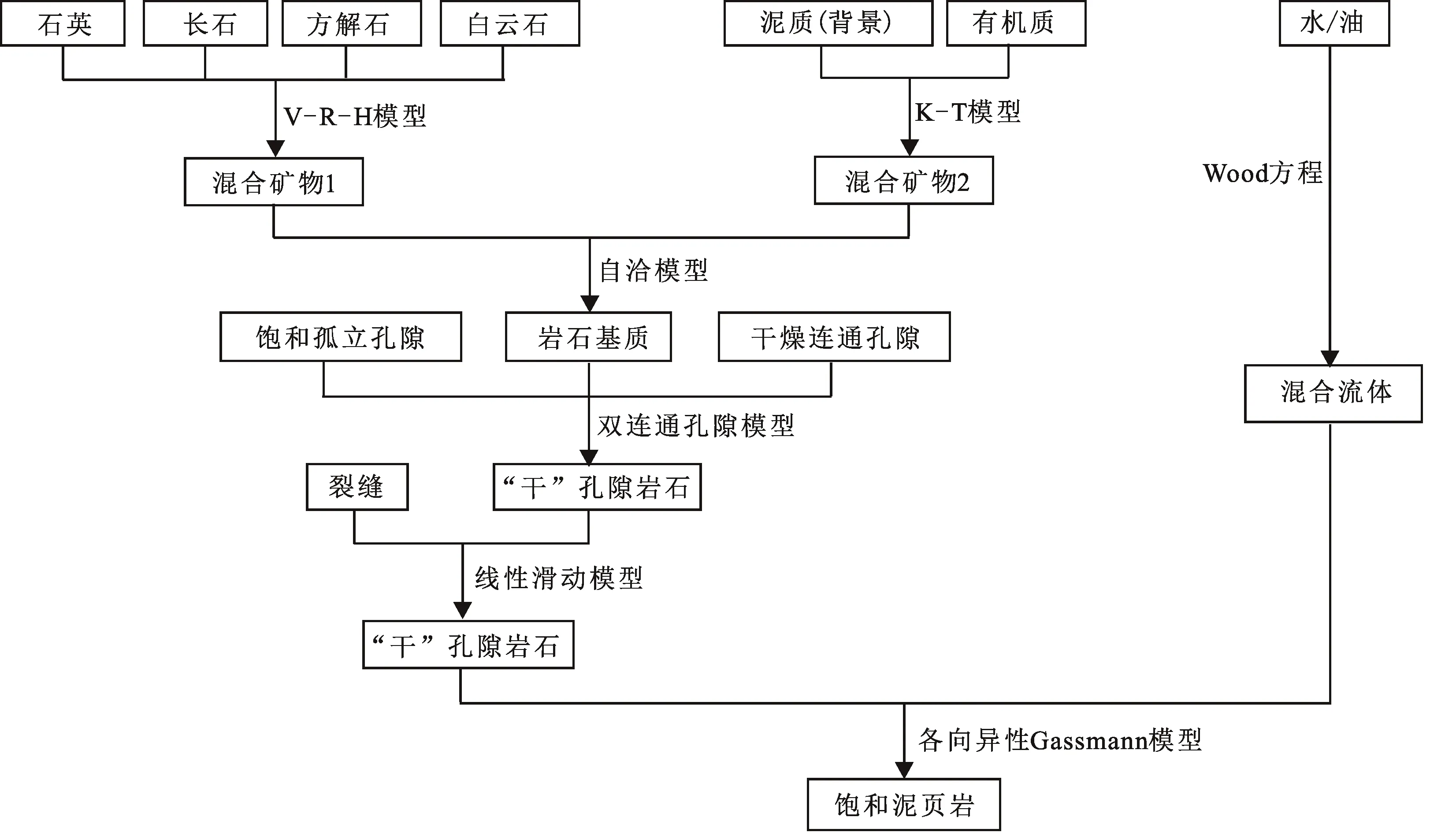
图3 泥页岩岩石物理建模流程Fig.3 Flow chart of mud shale rock physics model

2.1.2Kuster&Toksöz模型

Kuster & Toksöz模型[16]主要是应用长波一阶散射理论,考虑了包裹体体积分数、弹性性质和形状的影响,得到了一个应用广泛的双相介质有效模型。根据上述岩心样品扫描电镜照片观察可知,泥质是泥页岩中的主要基质矿物,有机质呈块状在其中分布,并且有机质中孔隙不发育,因此可以将有机质等效为球形包含物,利用Kuster & Toksöz模型添加到泥质背景中,其表达式为

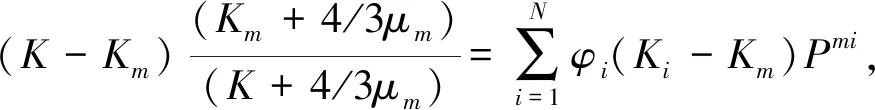
(2)

(3)

其中

式中,K、Km、Ki、μ、μm、μi分别是饱和岩石、岩石基质和第i种包含物的体积模量和剪切模量;φi为第i种包含物的体积分数;Pmi、Qmi表示在背景基质m中加入包含物材料i后的效果。

2.1.3 自洽模型

对于没有优势组分的介质,Budiansky与Hill[17-18]在Eshelby提出的应变能理论基础上,通过计算将包含物置于无限大背景材料产生的形变所引起的应变来估计岩石的体积模量和剪切模量,给出自洽模型。该模型考虑了彼此靠近的包含物的相互作用,适用于多种矿物共同作为岩石骨架的情况。混合矿物1和混合矿物2含量相当,没有绝对优势组分的介质,共同作为岩石骨架的组成部分,使用自洽模型混合最为合适。模型表达式如下:

(4)

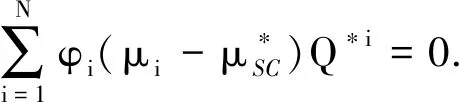
(5)

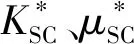
2.2 “干”孔隙岩石骨架弹性模量的求取

利用双连通孔隙模型将饱和孤立孔隙和干燥连通孔隙加入到岩石基质中,得到最初“干”孔隙岩石;在此基础上,利用线性滑动模型将干燥裂缝加入其中,得到最终的“干”孔隙岩石的弹性模量。

2.2.1 双连通孔隙模型

双连通孔隙模型[19]把孔隙分为以大孔隙为主的连通体系和以微孔为主的孤立体系,而且认为由两种以上不同平均孔隙半径的简单孔隙构成,从而建立孔隙结构模型。用连通系数来表示连通孔隙占总孔隙度的比例,能够表征岩石孔隙的整体连通性,用纵横比(孔隙长度和孔隙直径的比值)表示孔隙形态(刚性孔、柔性孔),用比例因子表示各种形态孔隙(连通刚性孔、连通柔性孔、孤立刚性孔、孤立柔性孔)的含量。古龙凹陷青山口组泥页岩储层微观孔隙主要包括原生粒间孔、次生溶蚀孔、晶间微孔、生物铸模孔和有机质孔,其中原生粒间孔和次生溶蚀孔连通性较好,晶间微孔、生物铸模孔和有机质孔的连通性较差,多呈孤立状存在,因此可以将微观孔隙分成以粒间孔和溶蚀孔为主的连通体系和以晶间微孔为主的孤立体系两大部分,利用双连通孔隙模型将连通孔隙和孤立孔隙加入到岩石基质中,得到“干”孔隙岩石。模型表达式如下:

φiso=φ-φcon=φ(1-ζ),

(6)

(7)

(8)

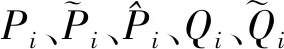
2.2.2 线性滑动模型

古龙凹陷青山口组泥页岩储层裂缝系统主要包括构造裂缝、成岩裂缝和层间缝,以构造裂缝为主,裂缝倾角普遍大于70°,发育少量的斜交缝和低角度裂缝。因此可以在以上“干”孔隙岩石骨架的基础之上,通过线性滑动理论[20]加入泥页岩储层的高角度裂缝,得到最终的“干”孔隙岩石骨架的弹性模型。其表达式如下:

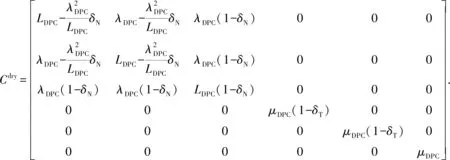
(9)

其中

式中,δN、δT分别为裂缝法向弱度和切向弱度;φf为裂缝孔隙度。

2.3 饱和岩石弹性参数的计算

古龙凹陷青山口组泥页岩储层镜质体反射率在0.9%～1.7%,处于成熟—高成熟生油阶段,孔隙流体包含油、水两相,因此可以利用Wood公式[21]对孔隙流体(油、水)进行混合,得到混合流体的体积模量;利用各向异性Gassmann方程[22]对模型进行孔隙流体充填,得到饱和流体的岩石物理模型弹性系数表达式,即

(10)

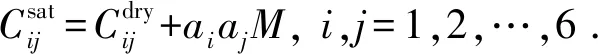
(11)

其中

式中,Ki、φi分别为第i种组分的体积模量和体积分数。

最后,利用纵横波相速度与弹性系数之间的关系式求得最终的饱和流体岩石的相速度。

3 储层参数影响因素

基于建立的复杂孔隙结构泥页岩岩石物理模型,系统分析有机质体积分数、裂缝孔隙度、基质孔隙度、孔隙纵横比和孔隙连通系数5种因素对岩石弹性参数的影响,为泥页岩岩石物理交会模板建立提供理论依据。所用的矿物及流体参数如表1所示。

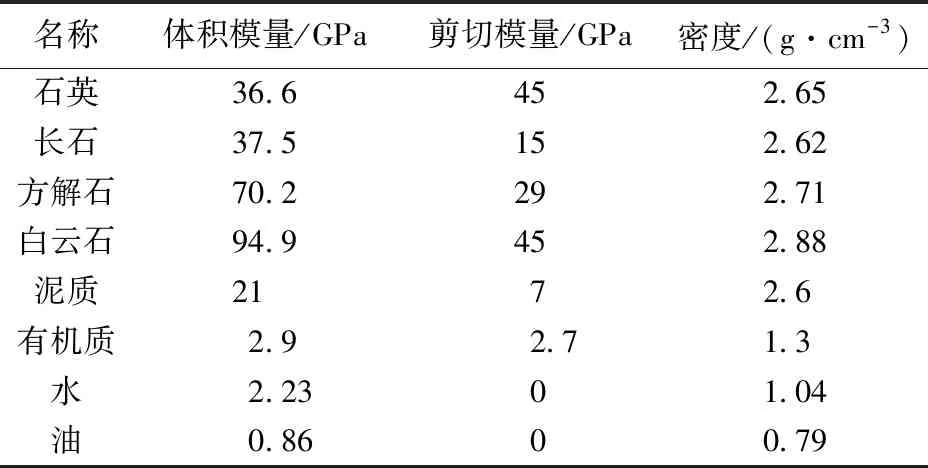
表1 矿物组分参数

3.1 有机质体积分数和裂缝孔隙度的影响

图4中给出了弹性参数随裂缝孔隙度φf和有机质体积分数φ0的变化,裂缝孔隙度的变化范围为0～0.01,有机质体积分数的变化范围是0～0.08,基质孔隙度为0。可以看出,随着裂缝孔隙度的增加,除泊松比外,其他的弹性参数均呈现减小的趋势;增加有机质体积分数,各弹性参数均减小,有机质体积分数的变化不会改变弹性参数随裂缝孔隙度的变化趋势。

图4 弹性参数随裂缝孔隙度和有机质体积分数变化Fig.4 Variation of elastic parameters with fracture porosity and organic volume fraction

3.2 基质孔隙度和孔隙纵横比的影响

图5中给出了弹性参数随基质孔隙度φm和孔隙纵横比的变化,基质孔隙度的变化范围是0～0.15,孔隙纵横比的变化范围是0.01～0.2,孔隙连通系数为0.5,裂缝孔隙度为0。可以看出,随着基质孔隙度的增加,除泊松比外,其他的弹性参数均呈现减小的趋势,其中孔隙纵横比取较小值0.01时,各弹性参数变化最为明显;增大孔隙纵横比,除泊松比外,其他的弹性参数均呈现增大的趋势,并且基质孔隙度越大,改变孔隙纵横比,各弹性参数变化越明显。

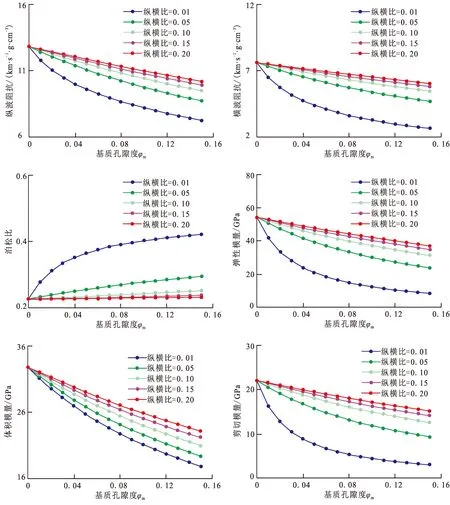
图5 弹性参数随基质孔隙度和孔隙纵横比变化Fig.5 Variation of elastic parameters with matrix porosity and pore aspect ratio

3.3 基质孔隙度和孔隙连通系数的影响

图6中给出了弹性参数随基质孔隙度φm和孔隙连通系数ζ的变化,基质孔隙度的变化范围是0～0.15,孔隙连通系数ζ的变化范围是0.1～0.7,刚性孔隙纵横比为0.1,柔性孔隙纵横比为0.01,裂缝孔隙度为0。可以看出,随着孔隙连通系数ζ的增加,横波阻抗和剪切模量保持不变,这主要是由于孔隙连通系数ζ的变化只改变泥页岩孔隙的连通性,不影响其孔隙形态、孔隙大小、流体成分和岩石骨架成分,其他弹性参数呈现减小的趋势但变化不明显。

图6 弹性参数随基质孔隙度和孔隙连通系数变化Fig.6 Variation of elastic parameters with matrix porosity and pore connectivity coefficient

4 岩石物理交会模板建立及速度预测

4.1 岩石物理交会模板建立

在泥页岩油储层评价过程中,有机质体积分数和总孔隙度起着重要的作用。有机质体积分数影响泥页岩的生油潜力、储集能力并进而决定了泥页岩储层的含油量及产能[23-24];孔隙体积决定了泥页岩油的储集空间[25]。因此需要优选出可以识别有机质和孔隙的敏感参数,再利用敏感参数进行泥页岩油储层岩石物理模板的构建。

基于上述建立的泥页岩岩石物理模型和弹性参数影响因素分析结果,分别比较纵波阻抗、纵横波速度比、弹性模量、泊松比、λρ和μρ等弹性参数受有机质体积分数和总孔隙度的影响,进行有机质和孔隙敏感参数的优选。图7是各弹性参数随有机质体积分数和总孔隙度的相对变化,可以看出,识别有机质的敏感参数从高到底分别为λρ、μρ、泊松比、纵波阻抗、弹性模量和纵横波速度比,识别总孔隙度的敏感参数从高到底分别是μρ、弹性模量、λρ、纵波阻抗、泊松比和纵横波速度比。通过对比优选,最终确定出λρ和μρ为识别有机质和孔隙的敏感参数,并且两者变化方向唯一、相关性较弱,可应用于泥页岩岩石物理模板的构建。

在构建过程中,以泥页岩岩石物理模型为依据,以λρ和μρ为横纵坐标,利用矿物组分含水饱和度模型[26]得到不同矿物组分含量下的含水饱和度曲线,用岩心测试分析数据对模板进行校正,调节各输入参数,从而建立基质矿物为石英、长石、方解石、白云石和黏土矿物,有机质体积分数为0、4%、8%和12%,总孔隙度为0～14%,孔隙流体为水和油的泥页岩岩石物理交会模板(图8)。由于研究区块内泥页岩中发育有含介形虫灰岩,因此在制作模板时建立了灰岩线(图8中黑色曲线),用于识别含介形虫灰岩和泥页岩。

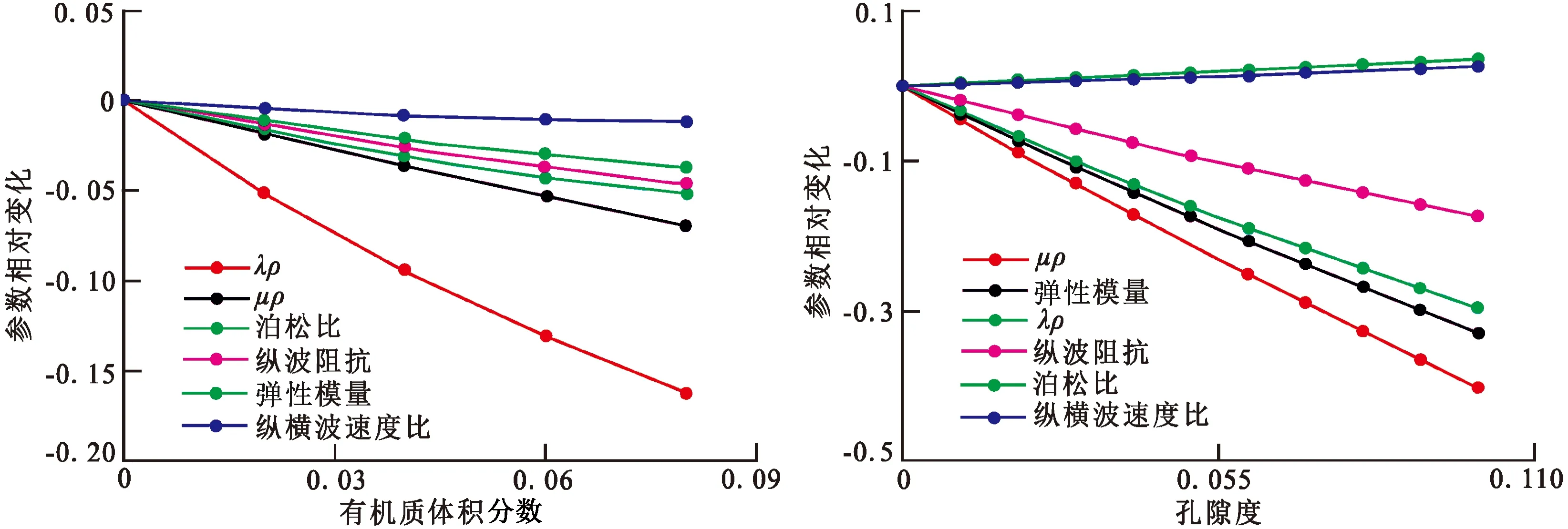
图7 有机质体积分数和孔隙度对各弹性参数的影响Fig.7 Impact of organic volume fraction and porosity on each parameter

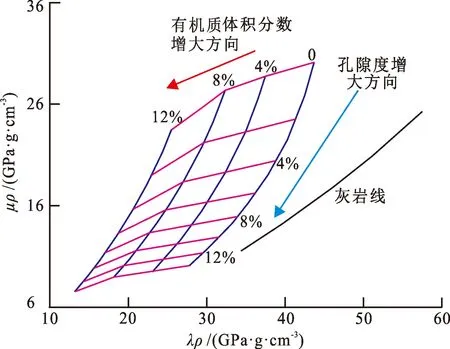
图8 泥页岩岩石物理模板Fig.8 Rock physics template of mud shale

利用松辽盆地北部青山口组经过岩心刻度的2口泥页岩井数据验证岩石物理模板的适用性。验证结果如图9所示,图中三角表示含介形虫灰岩,圆点表示泥页岩。可以看出,含介形虫灰岩主要分布在泥页岩线和灰岩线之间,不同有机质体积分数和不同孔隙度的实际数据点位置也与岩石物理模板结果基本一致,说明使用建立的岩石物理交会模板能较好地将泥页岩和含介形虫灰岩区分开来,并且该模板做到了不同有机质体积分数和不同孔隙度的有效区分,可以作为松辽盆地青山口组陆相泥页岩储层评价和“甜点”有利区识别的依据。

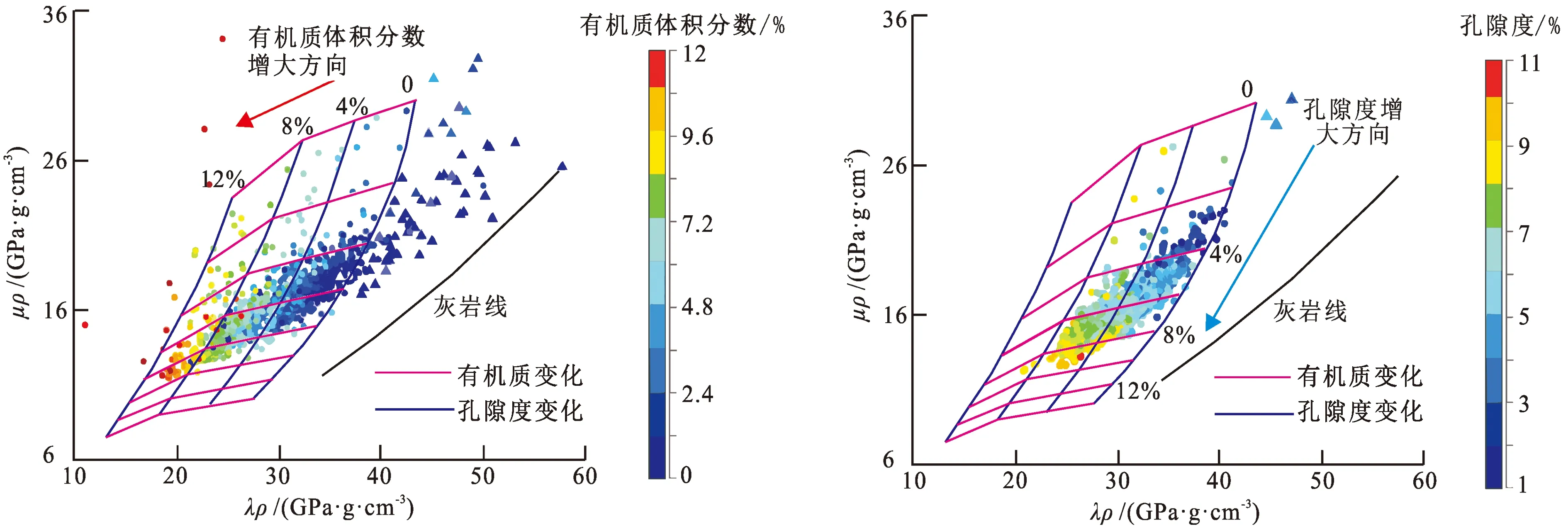
图9 岩心刻度的测井数据对岩石物理模板验证Fig.9 Verification of logging data on rock physics template

4.2 速度预测结果分析

利用建立的泥页岩岩石物理模型对松辽盆地北部青山口组某泥页岩井进行纵横波速度预测,分析该模型在实际泥页岩储层中的预测效果。井中各种矿物组分体积分数、有机质体积分数、基质孔隙度、裂缝孔隙度和饱和度信息通过测井解释并经岩心测试校正得到,孔隙连通系数由8块泥页岩样品经过核磁共振岩心实验分析得到,数值为0.48,孔隙纵横比依据岩心样品纳米CT扫描的3D图像统计结果得到,刚性孔隙纵横比为0.12,柔性孔隙纵横比为0.01。图10为预测的纵横波速度与实际测井曲线测量结果对比,可以看出,预测的纵横波速度与实测的纵横波速度变化趋势基本一致,吻合度较好,相对误差低于5%,从而保证了本文中提出的泥页岩岩石物理模型的可靠性和适用性。

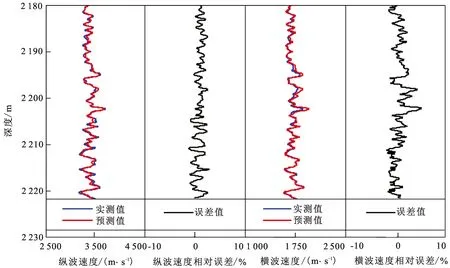
图10 预测的纵横波速度与实际测井曲线测量结果对比Fig.10 Comparison of prediction P(S)-wave velocity and actual logging data

5 结 论

(1)基于泥页岩基本地质特征分析,以岩石物理基础理论为依据,建立了一种考虑复杂孔隙结构的泥页岩地震岩石物理模型,经过实际测井数据验证,表明该模型对于松辽盆地北部青山口组复杂孔隙结构泥页岩纵横波速度预测是合理有效的。

(2)利用建立的泥页岩岩石物理模型,系统分析了有机质体积分数、裂缝孔隙度等5种因素对岩石弹性参数的影响,结果表明除了孔隙连通系数的影响较小外,其他因素的影响均较明显,为泥页岩岩石物理交会模板的建立提供理论依据。

(3)基于泥页岩岩石物理模型和弹性参数影响因素分析结果,优选出了对有机质和孔隙敏感的弹性参数λρ和μρ,构建了可指导实际应用的泥页岩岩石物理交会模板,该模板能较好地将泥页岩和含介形虫灰岩区分,且可实现不同有机质体积分数和不同孔隙度的有效区分。

(4)由于已钻井中缺乏裂缝发育层段,目前该模型对裂缝性质的影响分析,需要通过实际资料进一步验证。