基于手机数据的出行链推演算法

吴子啸

(中国城市规划设计研究院，北京 100037)

1 研究概述

1.1 手机数据类型及特征

与其他类型大数据类似，手机数据也是一种被动产生的痕迹数据，即用户使用手机进行通讯活动(通话、短信等)和运营商提供通讯服务的痕迹数据。由于手机痕迹数据包含位置和时间信息，从而提供了人们出行和活动的线索。与传统交通调查数据相比，手机数据具有大样本、可持续、成本低等优点，为未来交通研究和交通建模提供了全新的数据资源。

相关研究中通常将手机数据分为两类：一类是通话详单数据(Call Detail Record Data, CDR)，另一类是信令数据(Sightings Data)。CDR 数据是由用户使用手机进行通讯活动产生的痕迹数据，通常包含通讯活动的用户ID、起始时间、时长信息以及服务基站信息；信令数据是运营商提供通讯服务的痕迹数据，除了由用户进行通讯活动触发外，还可以由服务区切换等网络活动触发。与CDR 数据不同，信令数据中的位置信息通常为几个基站间通过三角算法计算的结果。因此，信令数据的时间密度和位置信息精度均高于CDR数据[1]。

手机数据的时间密度因用户而异，并且非常不规则。通常在某一小段时间内，手机数据密集出现，在较长且不规律的时间后，手机数据再次密集发生。为了表示手机数据的时间密度，通常将一天划分为以0.5 h 为单位的时段，在一个时段内有一个或多个手机数据即表示该时段出现手机数据，而以出现手机数据的时段数表示时间密度并据此计算手机数据出现的时间间隔。CDR数据的时间间隔可以达到数小时之久[2]，而信令数据的时间间隔通常也超过1 h[3]。本文采用某城市2015年的手机数据，以手机数据出现时段最多的15 h(大多数出行和活动集中的时段7:00—22:00)为研究周期，统计得到手机数据平均出现时段数量分布(见图1)。手机数据出现的时段数量平均为9.1 个，平均时间间隔为84 min，数据特征与已有文献中的描述基本吻合。预计未来随着智能手机用户比例的上升，手机数据的时间密度将会显著提高。

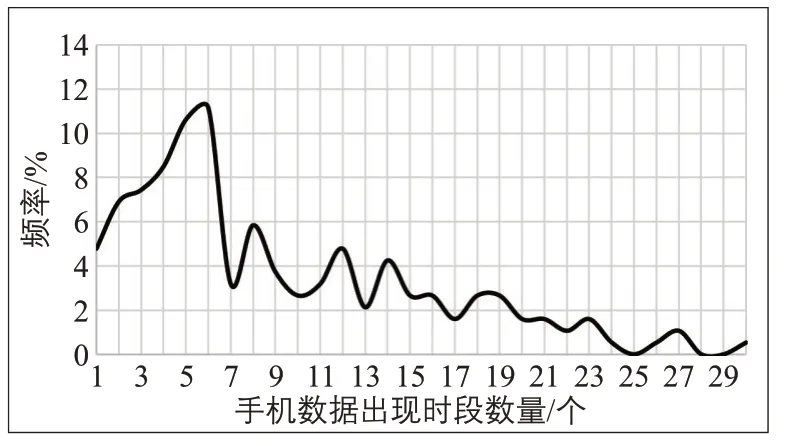
图1 手机数据的时间密度分布Fig.1 Time-density distribution of cell phone data

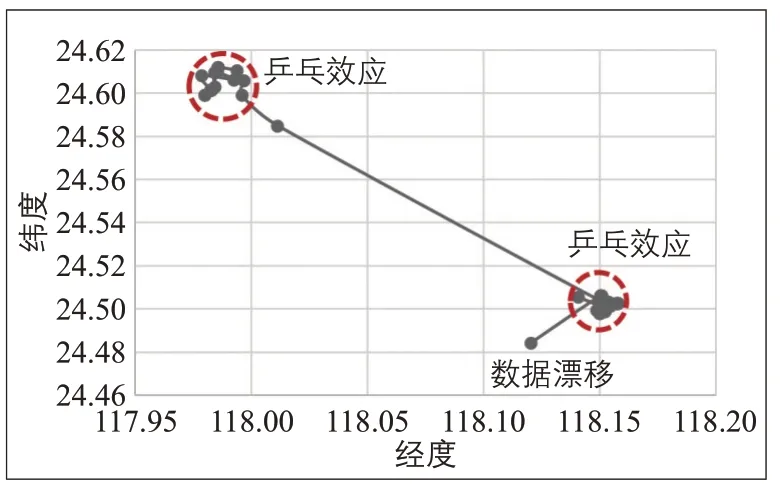
图2 手机数据误差示例Fig.2 Example of cell phone data error

根据大多数城市的居民出行调查结果，城市居民单次出行平均出行时耗大多集中在20～30 min。结合手机数据的平均时间间隔可以判断，由手机数据推演出行时耗的可靠性不高，并且一些出行活动也不能被手机数据所反映。

1.2 手机数据处理的关键问题

1）乒乓效应和数据漂移。

在通信网络覆盖的区域，通常一个具体地点会被周围几个基站的信号重叠覆盖。该区域内的手机所联系的基站会随各基站信号强度的变化而不断改变，从而产生在两个或多个基站间来回切换的现象，该现象被称为“乒乓效应”。另外，为保证手机用户通讯的效率与质量，服务基站往往有负荷优化的调节机制。当手机邻近的基站负荷较大时，手机信号会被自动切换至较远且负荷较小的基站，从而产生信号的漂移。因此，手机数据对地点的代表具有很大的不确定性。文献[4]对于信令数据的研究认为其在城市区域的位置误差在300 m 以内。文献[5]认为CDR 数据的位置误差可以从几百米到几千米，主要取决于基站的密度。如图2 所示，数据在两个主要活动地点有大量的乒乓效应并伴随数据漂移现象。文献[6]指出乒乓效应和数据漂移的数据约占数据总量的30%。

乒乓效应和数据漂移并不代表用户的真实移动，对这类数据进行处理是利用手机数据进行出行链推演的重要一环。在这方面研究中，已有三种方法被提出和应用。文献[7]提出基于速度的方法：即当基站(或位置点)A夹杂在基站(或位置点)B中并且由A至B的转换速度超过一个设定的极限值，则定义为乒乓效应。在手机数据的时间密度较低并存在空间不确定性的情况下，选择一个速度极限值是该方法的一个挑战。文献[6]和文献[8]则提出基于模式的方法，即根据乒乓效应的特征定义几个基站(或位置点)间切换的模式，当检测到该模式时即视为乒乓效应进行处理。由于实际中乒乓效应的形式非常多样，有时发生在两个基站间、有时发生在多个基站间，并间杂有数据漂移现象，因此，将所有乒乓效应的模式进行列举十分困难；另一方面，实际发生在两点之间的真实高频移动可能会被误以为乒乓效应。将以上两种方法结合而成的混合方法也是比较常见的应用[9]，但也无法完全避免各自方法内在的缺陷。

2）活动地点识别。

利用手机数据进行出行链推演的另一个关键点是对于活动地点的识别。一般认为，停留超过一定时间(通常为10 min)的位置点可以视为一个活动地点。由于手机数据的空间不确定性，需要将空间临近的位置点聚合在一点才能形成停留时间的累积。聚类算法通常用来实现这一目标。在众多聚类算法中，无须预设参数的基于距离的聚类算法[10-11]最受青睐。文献[5]提出另一种不需预设参数的聚类方法，即基于模型的聚类方法。但该方法对于时间密度稀疏的手机数据的运行效果并不理想[1]。显而易见，基于距离的聚类算法的结果容易受到数据漂移的影响。例如，在几个时间相继、空间临近的位置点中夹杂一个较远距离的数据漂移，聚类的结果将由一个类(位置点集合)变成三个类，漂移数据成为其中单独的一类。这显然会影响位置点停留时间的累积，进而影响活动地点的识别。

文献[12-15]提出一种改进的基于距离的聚类算法，即随着类中位置点的增加，重新计算类的型心。这种改进方法可以在一定限度上提高算法对乒乓效应和漂移数据的容忍度，但算法有效性仍然会受到数据空间不确定性的影响。

手机数据的预处理与活动地点的识别相互依赖、相互影响。大量乒乓效应和数据漂移会影响活动地点识别算法的效率和准确性。因此，在大多数处理CDR 数据的流程中，先进行手机数据的预处理[16]，再执行聚类算法进行活动地点识别。而对于信令数据，文献[1]认为应先执行聚类算法消除空间不确定性，才能有效识别和处理乒乓效应。迄今为止，众多研究在城市层面上基于手机数据进行活动和出行链的推算[1,16]，但算法在个体数据层面的有效性从未详细探讨。手机数据乒乓效应和漂移的内在规律目前仍不明确，对这些数据预处理方法的有效性也难以评价。与以往研究不同，本文提出一种新的方法——时空贪婪同化法，该方法更多地利用了人们出行和活动的一般规律以及手机数据在某一时段密集出现的特征，最大限度地消除手机数据的空间不确定性。另外，改进的空间聚类算法在进行类型心更新时，考虑了位置点的停留时长，能够更加有效地锚固居住地、工作地等人们长时间停留的活动点，从而更加准确地推算出行链。

2 算法描述

本文提出基于手机数据推演出行链的算法流程，如图3所示。

2.1 数据初始化

数据初始化的步骤主要包括：1)对手机数据进行栅格化处理，以栅格型心经纬度取代落在栅格内各位置点的经纬度。手机数据位置点从本源上均是基于基站定位的，而手机基站经纬度通常有保密性要求，栅格化处理一方面可以实现保密的目的，另一方面，不同数据源(如基于基站定位的数据和基于三角定位的数据)可进行融合处理。2)建立各位置点的开始时间和结束时间项。有些手机信令数据既给出信令开始时间也给出了信令结束时间。在只给出信令开始时间时，可以在开始时间上加一个极小的时间段(如20 s)生成信令结束时间，这样手机时空数据的一条记录可表示为li表示第i条数据记录的位置点，tis和tif分别表示第i条数据记录的开始时间和结束时间，数据记录集合为N。3)按开始时间对所有数据记录进行排序，合并同一位置点的相邻数据记录。也就是说，将同一位置点的所有相邻数据记录合并为一条新记录，新记录的开始时间设为被合并数据记录中开始时间的最小值，结束时间设为这些数据记录中结束时间的最大值。

2.2 时空贪婪同化

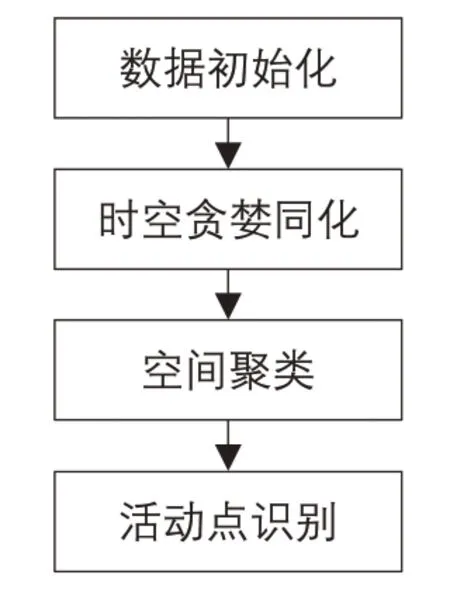
图3 算法流程Fig.3 Algorithm process

时空贪婪同化的基本思想是依次从当前数据记录集中找出最频繁出现的位置点(即数据记录最多的位置点)，识别短时间内夹杂在该位置点的两条数据记录间的其他位置点，形成位置点集合进行同化。由于借鉴了贪婪算法的思想，该步骤被称为时空贪婪同化流程。具体算法如下：

1）将初始化的数据记录集N设为当前数据记录集，时间段集合T设为空集；

2）从当前数据记录集中找出数据记录最多的位置点m，提取位置点m的所有数据记录生成数据记录子集Nm={mj,tjs,tjf}，并生成位置点集合Cm={m}；

3）从Nm中第一条记录开始，若当前数据记录的结束时间距下一条记录的开始时间的间隔小于等于τ，即(t(j+1)s-tjf)≤τ，则更新时间段集合T=⋃j(tjf,t(j+1)s)，执行完毕生成时间段集合T；

4）对于当前数据记录集N中的每一条数据记录(li,tis,tif)，若(tis,tif)⊆T并且li不在位置点集合Cm中，则将li加入Cm中，执行完毕生成位置点集合Cm，并计算Cm的型心经纬度，即为其所包含的各位置点经纬度的加权平均值，权重为各位置点在数据记录集N中出现的频率或累积停留时间；

5）去除当前数据记录集N中位置点属于Cm的所有记录，返回步骤2)；循环结束生成位置点集合C={Cm}；

6）将原数据记录集N中位置点属于Cm的所有记录替代为Cm的型心，然后将同一位置点的所有相邻数据记录合并为一条新记录，新记录的开始时间设为这些数据记录中开始时间的最小值，结束时间设为这些数据记录中结束时间的最大值。执行完毕生成数据记录集N′。

在上述算法中，依次从空间位置点最多的数据记录开始处理，这些位置点通常为手机用户居住和就业所在地以及经常访问地点，这样不仅保证算法有很高的计算效率，也有助于锚固这些经常访问的活动点。步骤3)中时间间隔τ可取15 min。根据各城市的居民出行调查结果，一次出行的时耗通常在5 min以上，而在出行目的地活动所花时间一般在5 min 以上。从一个地点出行再返回原地的过程涉及一个活动和两次出行，因此最小时间间隔应为15 min以上。另外，由于手机信令数据通常会在某些时段密集发生，尤其是发生乒乓效应和数据漂移时，那么通过上述步骤对夹杂数据进行搜索同化后，手机数据的空间不确定性将在很大限度上被消除。

2.3 空间聚类

空间聚类是对当前数据记录集的空间位置点按聚类算法进行分类，改进的聚类算法如下：

1）将上一阶段结果N′设为当前数据记录集，计算各位置点l的总停留时间Tl=∑i∈Il(tif-tis)，Il为数据记录集中位置点为l的序列号集合，按总停留时间由大到小对各位置点排序，形成位置点集合L={l1,l2,…,lk}；

2）在L中按顺序取li进入类Ch，li为Ch型心，依次计算L中其他位置点lj至Ch型心的距离Dis(lj,Ch)，若 Dis(lj,Ch)＜δ，则将lj加入Ch，更新Ch型心的经纬度为Ch中各位置点经纬度的加权平均值，权重为各位置点的总停留时间；否则继续进行，直到L中任意一点至Ch型心的距离不小于δ，生成类Ch；

3）从L中删除Ch中所含位置点，若L不为空，返回步骤2)。否则输出类{C1,C2,…,Cf}；

4）在N′数据记录中，将各位置点替换为其所属的类型心；然后将同一位置点的所有相邻数据记录合并为一条新记录，新记录的开始时间设为这些数据记录中开始时间的最小值，结束时间设为这些数据记录中结束时间的最大值，最后得到结果数据记录集N′。

上面的空间聚类方法实质上是一种渐进聚类算法[13]的改进算法。渐进聚类算法会因位置点的不同排列次序而产生不同的聚类结果，文献[1]选择K-means聚类方法来克服这一缺点。但K-means聚类方法的预设参数需要经过试算才能确定，会极大地影响计算效率。本文提出的方法先对位置点按停留时间进行排序，聚类始终从长时间活动的位置点发起，保证了聚类结果的唯一性和合理性。另外，类型心更新的机制中引入了位置点停留时间的权重，更加锚固了长时间停留点的位置。大多数的出行距离为500 m 以上，步骤2)中δ可取200～500 m。

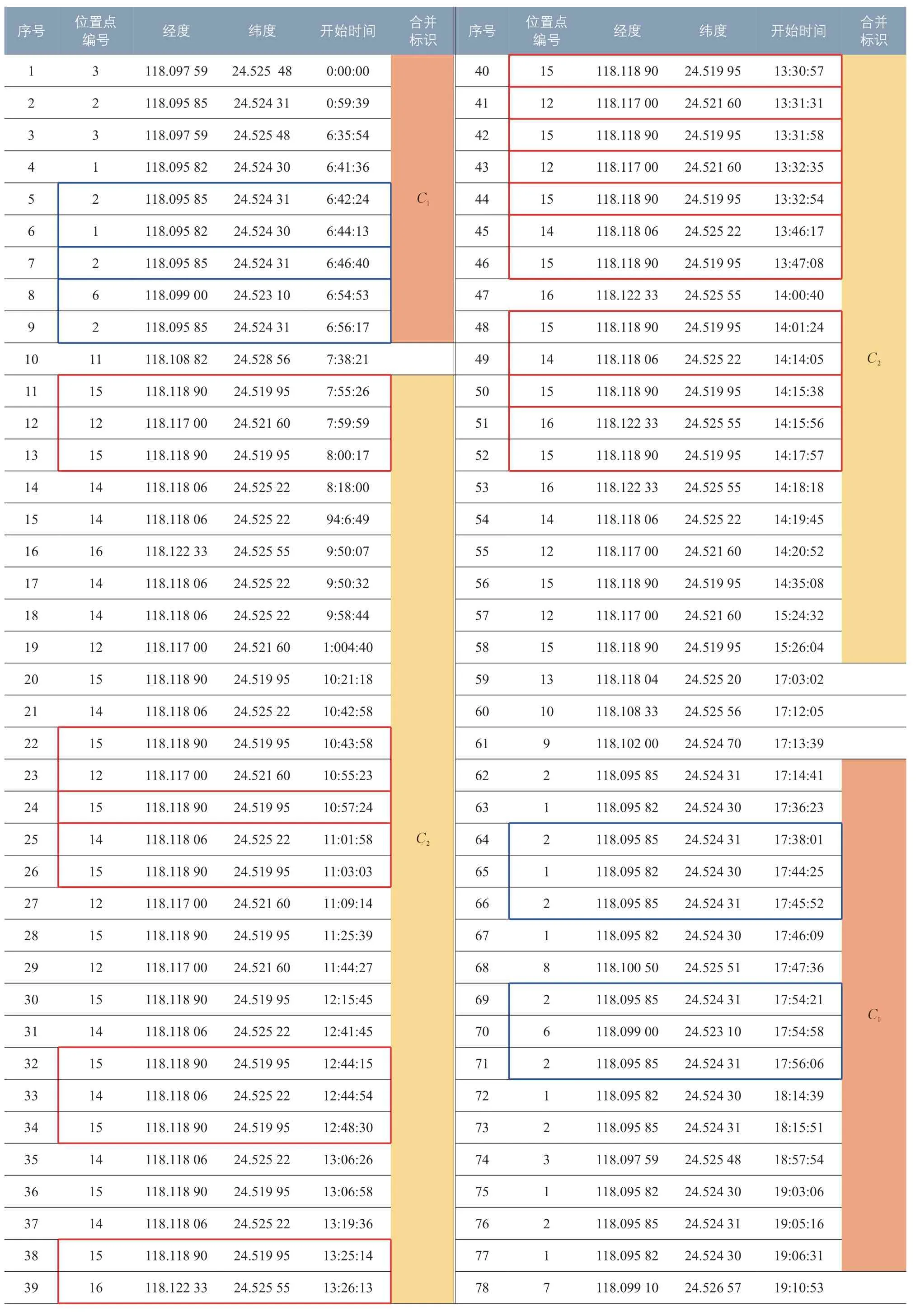
表1 手机数据原始记录Tab.1 Original raw cell phone data

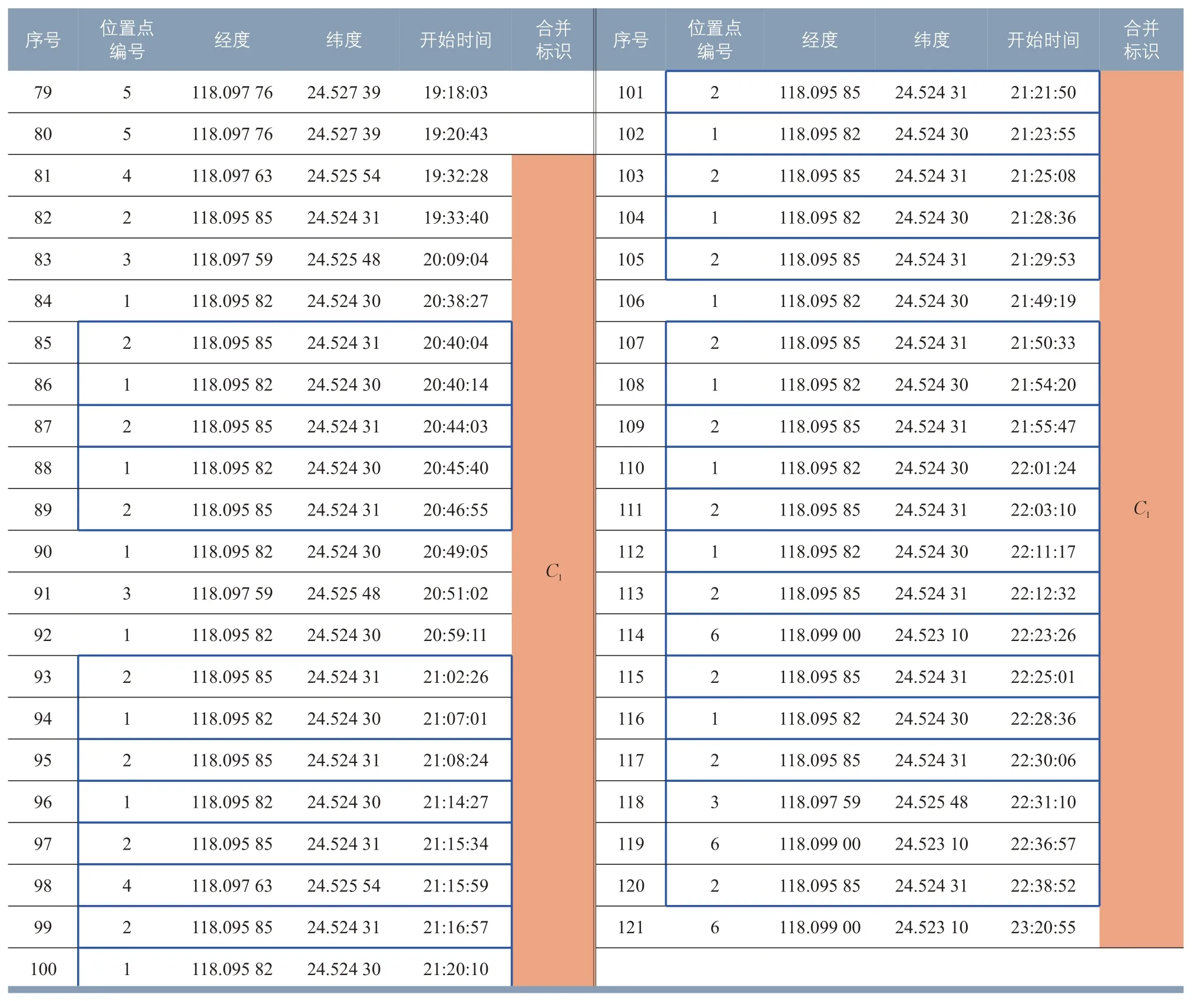
续表

2.4 活动点识别

活动点识别指辨认用户活动地点，一般将单次停留时间超过一定值(如5 min)的位置点作为活动点。在时空贪婪同化和空间聚类步骤之后，存在活动的位置点能够最大限度地累积到停留时间，便于活动点的识别。

3 算例

表1 为随机抽取的匿名用户一天的手机数据，共121 条，表中序号按数据开始时间排序，位置点共计16 个(见表2)，位置点编号按各位置点经度由小到大排序。可以看出，出现次数最多的位置点编号为2，表1中蓝色框表示相邻两条位置点为2 的数据记录满足开始时间小于15 min的条件，红色框表示相邻两条位置点为15 的数据记录满足开始时间小于15 min的条件。

根据时空贪婪同化流程建立位置点集合C1={1 ,2,3,4,6}。同理，对应于位置点15(见 表 1 中 红 色框)，可 以 得 到C2={12,14,15,16}。表1 中合并标识表示这些数据记录的位置点属于同一个位置点集合，将被集合型心所取代。时空贪婪同化流程的结果如表3 所示。为直观对比，表3 中序号与表1 保持一致，合并的数据记录保留了起始数据记录序号。

为说明算法的有效性和计算效率，同时采用K-means 聚类方法对以上数据进行处理，结果如图4 所示。K-means 聚类方法(δ取500 m)的结果生成3个类，按文献[1]提出的处理框架，类C2与C3将在接下来的步骤中被检测为乒乓效应而进行合并，从而得到与时空贪婪同化流程完全类似的结果。但K-means 聚类方法需要计算两点之间的空间距离，本质上是一种O(|N|2)算法( |N|为初始数据记录条数)，而时空贪婪同化流程为O(|N|)算法，计算量远远小于前者。

基于K-means 聚类方法[1]得到的类C1={1 ,2,3,4,5,6,7,8} 会 因δ取 值 而 变化，从用户多日的数据分析来看，时空贪婪同化流程得到的C1={1 ,2,3,4,6} 能更客观地反映用户居住地的位置。位置点1，3，4，6夹杂在相邻两条位置点为2的记录中的最小时间间隔分别为2 min 52 s，8 min 46 s，1 min 23 s 和1 min 45 s。也就是说，只要时间间隔τ取10 min 以上时，C1即可包含位置点1，2，3，4，6。另一方面，位置点5，7 和8 夹杂在相邻两条位置点为2 的记录中的最小时间间隔分别为27 min 9 s，27 min 9 s和1 min 20 s，当τ取17～27 min时，位置点8将进入C1；当τ取28 min以上时，位置点5和7将进入C1。由于C1型心计算会以各位置点停留时间为权重，位置点8，5和7进入C1对于型心位置的影响很小。由此可以看出，只要τ在一定范围内，时空贪婪同化流程的结果相当稳定。

从表3 可以看出，经过时空贪婪同化流程，121条原始数据记录被精简至10条，计算量远远小于各种空间聚类算法，且原始数据记录中各种形式的乒乓效应完全被消除，位置点C1和C2的停留时间得到最大限度的累积。不难推测，C1为居住地，而C2为工作地，位置点11 为上班途中留下的痕迹，而位置点13，10 和9 为下班途中留下的痕迹。位置点7 和5 可能表征一次基于家的活动，但由于出行距离较短，在接下来的空间聚类流程中可能会被抹去(取决于聚类所采用的参数)。

虽然从这个具体例子来看，在时空贪婪同化流程之后进行空间聚类并非十分必要，但由于数据记录已大幅精简，改进后的空间聚类的计算量非常小。况且手机数据产生漂移和乒乓效应的情形多种多样，保留空间聚类流程可以弥补时空贪婪同化流程可能力不能及的地方。从表3可以看出，位置点13在空间聚类流程中进入C2，这虽然无助于提升对于停留点位置的判断，但是能够提升对于离开工作地时间判断的精度。

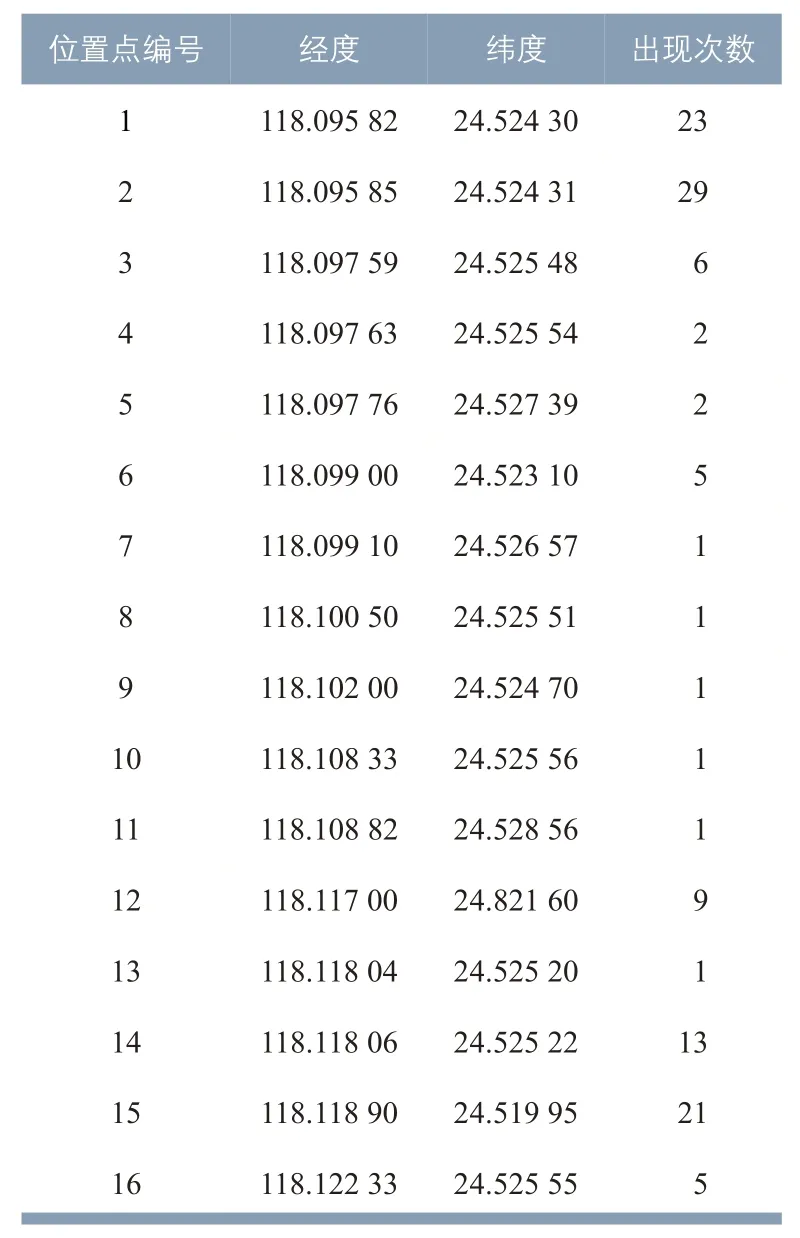
表2 各位置点经纬度及出现次数Tab.2 The latitude and longitude of different location point and its occurrences

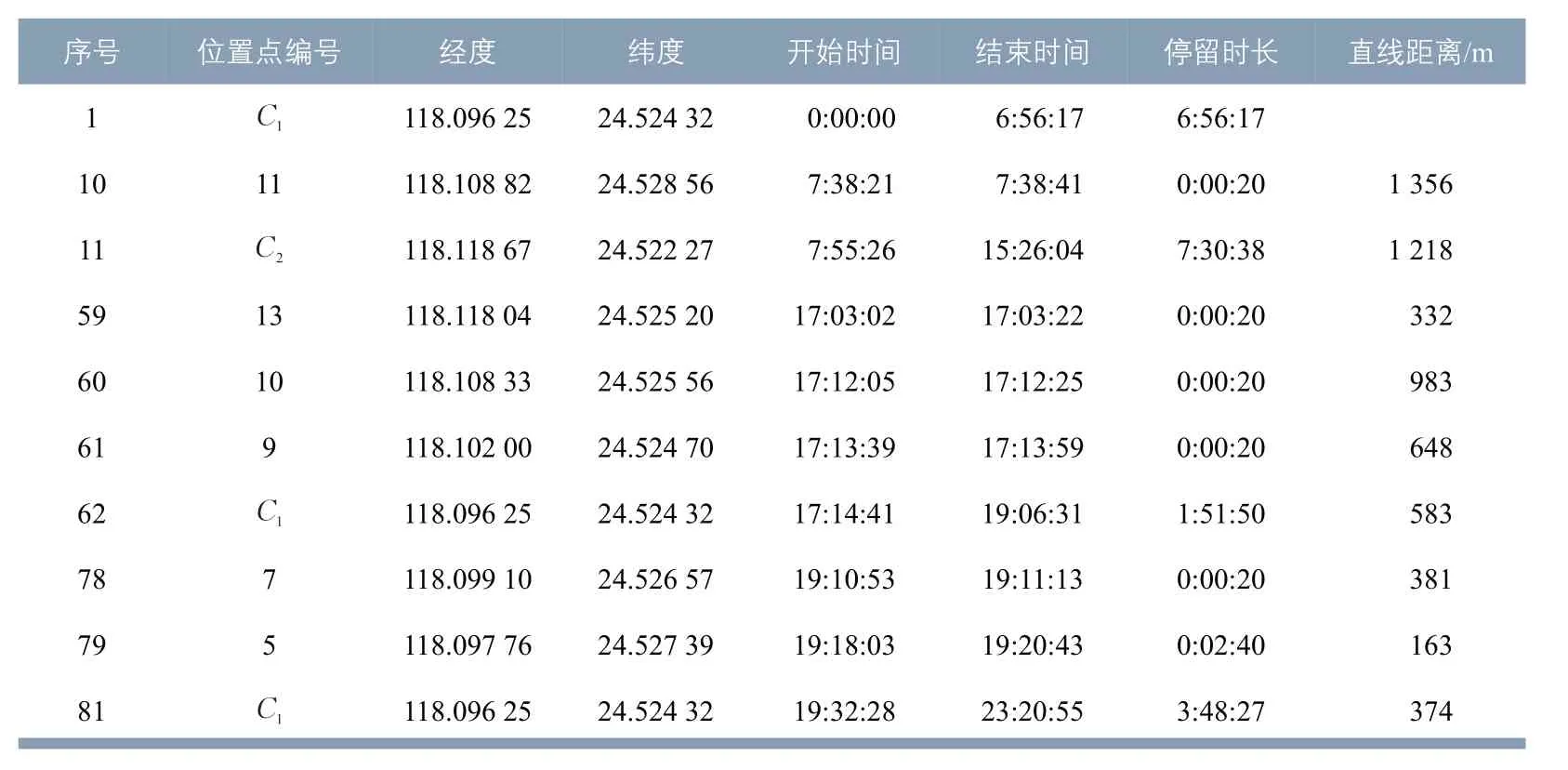
表3 时空贪婪同化流程处理结果Tab.3 Results of space-time greedy assimilation process

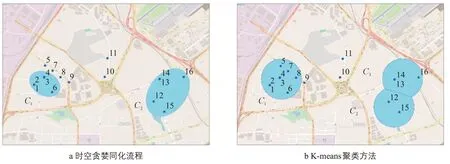
图4 算法结果比较Fig.4 Results of different algorithms

4 结语

与各种基于空间紧密性的聚类算法不同，本文提出一种基于时间紧密性的新算法——时空贪婪同化流程，用于从手机数据推演出行链。在随机抽取的个体手机数据测试中，新算法表现出很高的效率，对于居住地、工作地等停留较长时间的活动点的锚固作用尤其明显。由于篇幅限制算例是针对一天的手机数据，显然算法无须调整即可应用于多天手机数据。未来的研究将集中在整个城市层面居民出行链的推演以及推演结果与交通调查数据的比对方面。