一种高时频聚集性的方法在非平稳信号分析中的应用

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

0 引言

非平稳信号遍布生产生活各个领域，如机械故障信号、语音信号、通信信号、生物医学信号、地质勘探信号、雷达探测信号等等均属于非平稳信号。传统的时域和频域分析方法不能兼顾信号在时域和频域的局部化特征，而这些特征恰好反映非平稳信号的本质，时频分析方法既能反映信号的频率信息，又能反映频率随时间的变化规律，因此，时频分析方法成为处理非平稳信号的有效手段。主要的时频分析方法包括：Gabor变换、短时Fourier变换(STFT)、小波变换(WT)、Wigner-Ville分布(WVD)、自适应信号分解方法等，然而受Heisenberg测不准原理、交叉项干扰及模态混叠等的影响，很多方法时频分辨率很低，不能准确分析非平稳信号的时变特征。

为提高时频分布的时频分辨率，Auger et al[1]提出时频重排算法，利用重排算子将时频能量重新分配，使能量重心聚集在信号的瞬时频率脊线附近，有效提高了时频聚集性，但计算量较大。Daubechies et al[2]提出了同步压缩小波变换(synchrosqueezing wavelet transform, SST)，其本质是小波变换与时频重排技术的结合，对小波变换后时频分布在频率/尺度方向进行压缩，以达到更高的时频聚集性，相比于重排技术，同步压缩小波变换计算速度快，且支持信号的重构。此方法自被提出以来，大量学者对此给予关注，并展开了一系列深入研究，同时将其应用到机械故障诊断、地震探测信号分析、土木结构识别、语音信号识别等多个领域。Chuan et al[3]指出由于同步压缩小波变换仅在频率域上进行压缩变换，在时间域上没有处理，这就导致其对强调频信号分析时会发生能量的扩散，时频聚集性下降，提出广义同步压缩变换，并用于齿轮故障诊断中。Feng et al[4]认为同步压缩小波变换在处理多分量信号时会存在频率混叠问题，提出迭代解调分析法，以得到精确的时频谱，并应用于行星齿轮箱故障诊断中。Wang et al[5]提出匹配同步压缩法用于处理快速变化的多分量信号，并应用于机械故障诊断。刘景良等[6-7]将同步压缩小波变换引入土木工程领域，用来识别结构的瞬时频率，并采用解析模态分解方法改进同步压缩性能。汪祥莉等[8]利用同步压缩小波变换处理混沌干扰下的谐波信号提取，取得了良好效果。金艳等[9]将同步压缩变换扩展到同步压缩Chirplet，结合分数低阶方法处理复杂噪声干扰下线性调频信号参数估计问题。于刚[10]提出同步提取方法来改进同步压缩小波变换的抗噪性能，用于挖掘机振声信号时频分析。Iatsenko et al[11]对同步压缩小波变换在瞬时频率估计以及信号重构方面做出了探索。由此可见，作为一种改良的基础时频分析方法，同步压缩小波变换有很大的挖掘潜力以及广阔的应用空间，对其进行深入研究是有必要、有价值的。现有文献还没有对此方法进行全面、透彻分析，所以本文针对几种典型非平稳信号对同步压缩小波变换进行全方位的探讨，并与短时傅里叶变换和连续小波变换这两种传统时频分析对比分析，此工作对时频分析领域将有很好的指导意义。

1 同步压缩小波变换

Daubechies提出的同步压缩小波变换是从连续小波变换(CWT)出发的，首先对信号进行连续小波变换，再进行时频重排，对小波系数进行压缩变换，使得时频分布更清晰、时频分辨率更高。假设一个多分量谐波信号x(t)为

(1)

式中，Ak(t)>0，φk′ (t)>0，且信号的幅值Ak(t)变化比频率φk′ (t)变化缓慢，同步压缩小波变换可以准确分析此类信号的时频特征，精确提取各分量的频率成分。

首先对于给定的母小波函数Φ对信号进行连续小波变换如下

(2)

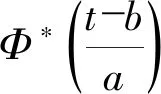
Daubechies从一个纯粹的谐波信号开始分析同步压缩小波变换，首先对谐波信号进行小波变换得到的小波系数会聚集在原信号的频率附近，并且振荡频率与原信号也相同，所以通过计算各小波系数的振荡频率对原信号频率进行估计，再利用压缩算子将频率相同的小波系数压缩到一起，可以明显提高时频分布的时频聚集性。这里以一个幅值恒定的谐波信号s(t)为例进行阐述。

s(t)=Acos(ωt)

(3)

其连续小波变换为

(4)

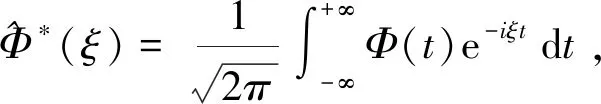
(5)

式中，∂bWs(a,b)为Ws(a,b)对b的一阶偏导。

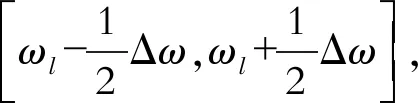
(6)

同步压缩的实质就是将小波变换系数在频率/尺度方向的扩散区域压缩至一个以ωl为中心的集中区域，以达到提高时频聚集性的目的。

2 仿真信号分析

为了全面分析同步压缩小波变换，下面将分别从单分量信号与多分量信号两大类出发，其中涉及谐波信号和强调频信号成分，并分析信噪比对同步压缩小波变换的影响，通过Rényi熵评价时频聚集性，同时与短时傅里叶变换和连续小波变换做对比。本文中同步压缩变换统一采用Morlet小波。

2.1 单分量信号分析

为了简洁，采用分段信号s(t)进行分析，其中，0～6 s为调频信号，6～12 s为谐波信号，表达式如下

(7)

采样频率100 Hz。图1至图4分别为无噪声、SNR=5、SNR=0、SNR=-5情况下几种时频分析方法对比图。SNR表示信噪比，计算式如下

(8)

式中，Ps和PN分别表示信号和噪声的有效功率。

由图1可以看出，在无噪声情况下，STFT和CWT虽然能识别信号的频率成分，但时频谱聚集性很差，SST时频聚集性非常高，能够清晰显示调频分量和谐波分量。由图2～图4可以看出，STFT和SST受噪声干扰非常严重，在信噪比逐渐减小的情况下，其时频分布越来越模糊，最后已经不能识别信号成分，而SST由于将时频系数进行压缩变换使时频聚集性提高，受噪声影响较小，在低信噪比下仍能保持高时频聚集性。

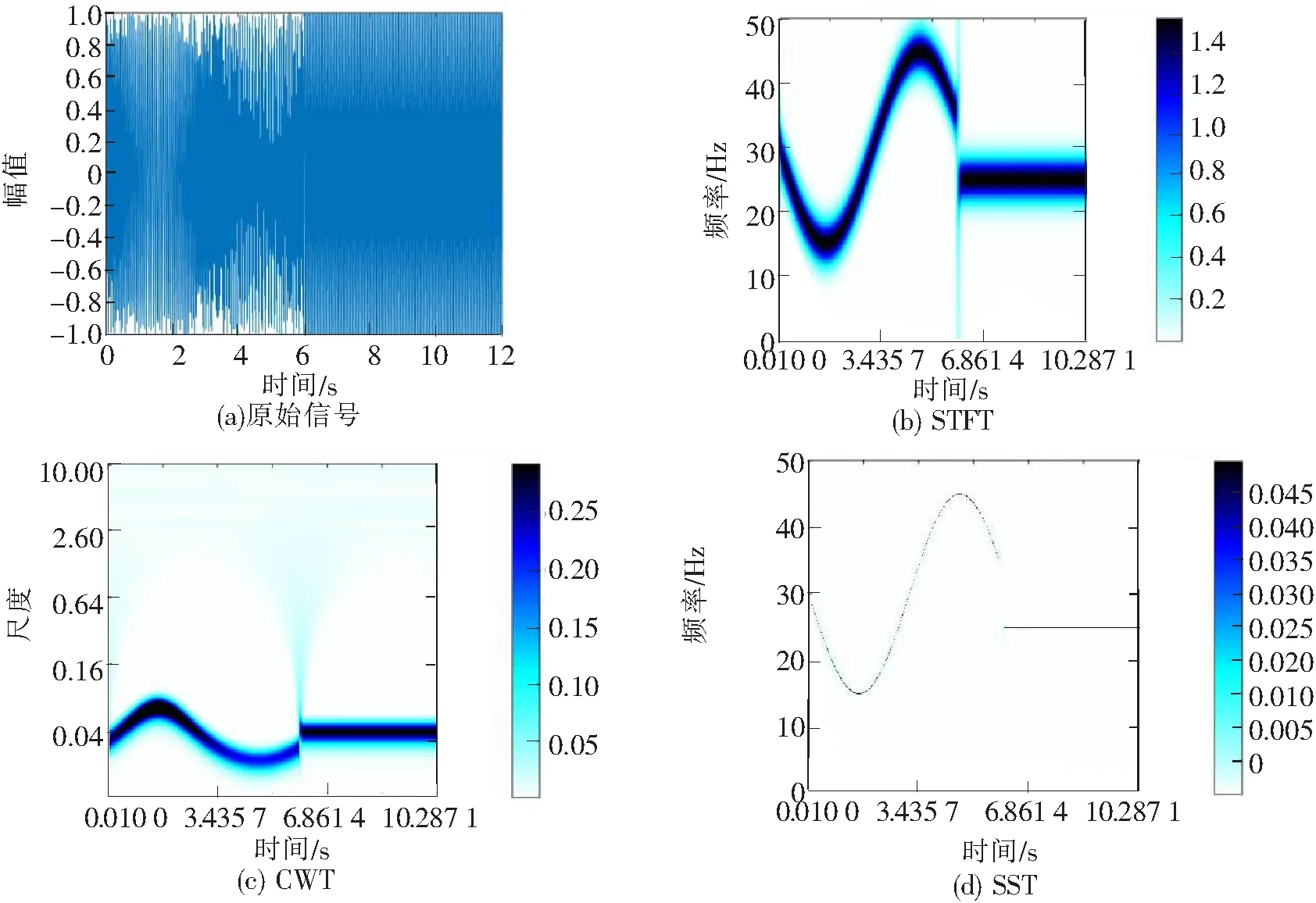
图1 无噪声情况下几种时频分析对比图(单分量)

图2 SNR=5时几种时频分析方法对比图(单分量)

图3 SNR=0时几种时频分析方法对比图(单分量)

图4 SNR=-5几种时频分析方法对比图(单分量)

Rényi熵可以客观评价时频聚集性的好坏，Rényi熵值越小表示时频聚集性越高，表1列出了不同信噪比下几种时频分析方法的Rényi熵值。由表1可以看出，3种时频分析方法Rényi熵随信噪比减小而增加，表明时频聚集性随信噪比减小而变弱。在各信噪比情况下，3种方法时频聚集性关系为：SST>STFT>CWT。综上所述，SST在时频聚集性上较传统的STFT和CWT显著提高。

表1 单分量信号不同信噪比下几种时频分析方法的Rényi熵

2.2 多分量信号分析

为了使所分析信号更具广泛性，此处选择一个幅值调制的线性调频信号和一个余弦和线性混合调制的调频信号相叠加，多分量信号s(t)表达式如下

s(t)=cos(2π(0.1t2.6+3sin(2t)+10t))+e-0.2tcos(2π(40t+t2.3))

(9)

采样时间为10 s，采样点数2 000。

图5至图8分别为无噪声、SNR=5、SNR=0、SNR=-5情况下几种时频分析方法对比图。由图可见，对于多分量信号，STFT和CWT仍然存在能量发散，时频聚集性差的问题，且随着信噪比降低，对于线性调频信号已无法识别，余弦调制信号也基本被淹没在噪声中。SST在无噪声情况下，时频聚集性仍然良好，由图5(d)～图8(d)可以看出，随着噪声干扰增强，SST的时频聚集性基本不受影响，仍能清晰显示各频率分量，可见其对于强调频信号仍然有效。

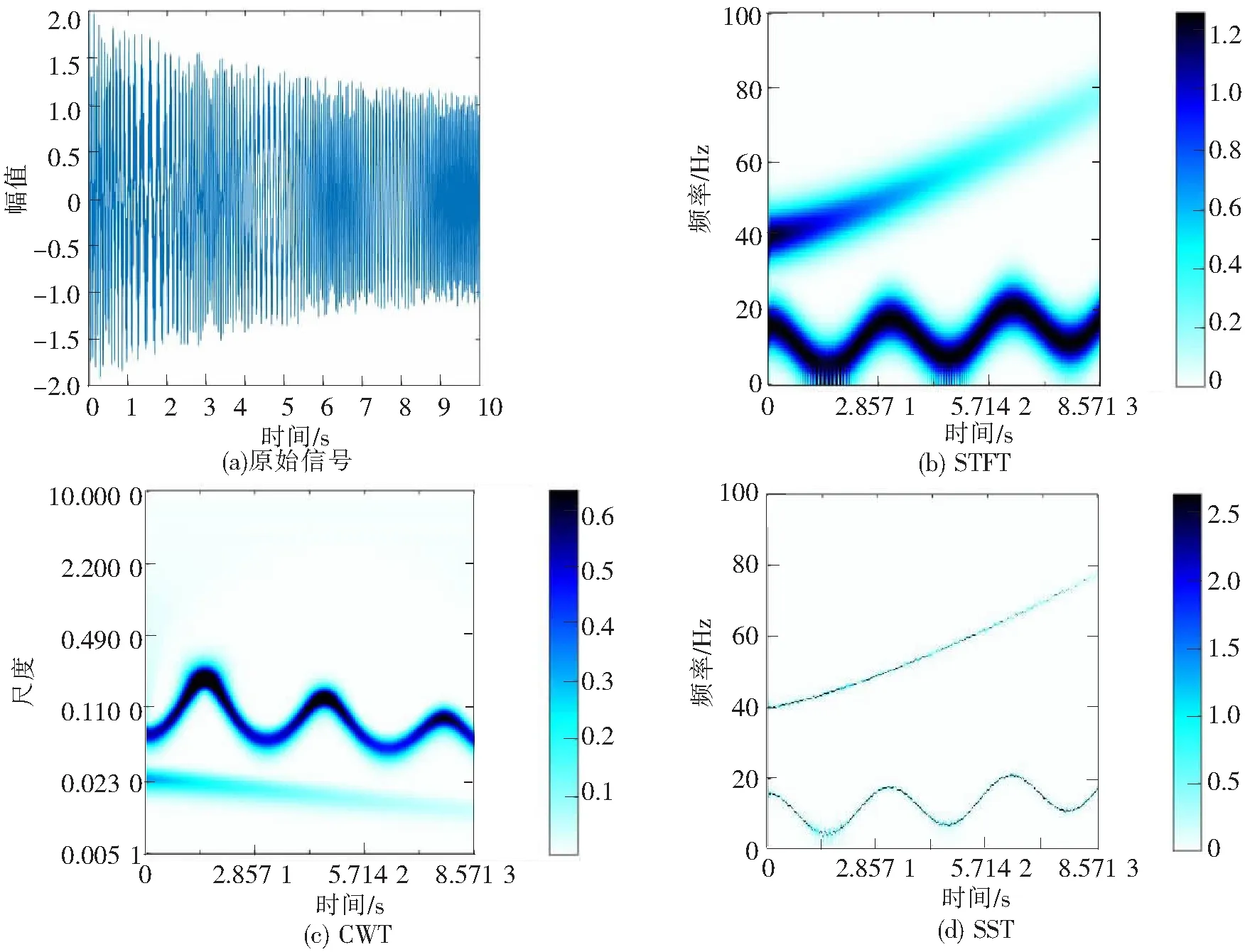
图5 无噪声情况下几种时频分析对比图(多分量)

图6 SNR=5情况下几种时频分析对比图(多分量)

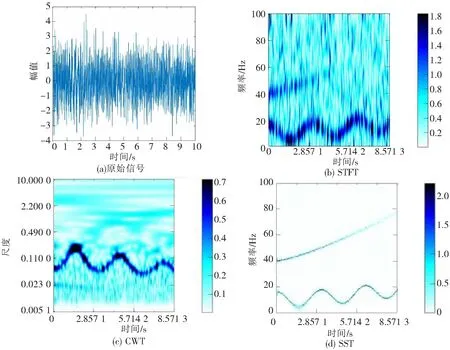
图7 SNR=0情况下几种时频分析对比图(多分量)

图8 SNR=-5情况下几种时频分析对比图(多分量)

同样用Rényi熵评价这几种方法处理多分量信号的时频聚集性，Rényi熵结果如表2所示。由表2可以看出，3种时频分析方法Rényi熵仍然与信噪比呈负相关，时频聚集性随信噪比减小而变弱。在各信噪比情况下，3种方法时频聚集性关系为：SST> CWT>STFT。通过与表1对比可以发现，这3种时频分析方法在处理多分量信号时的时频聚集性均比单分量信号的时频聚集性稍差。

表2 多分量信号不同信噪比下几种时频分析方法的Rényi熵

3 实验分析

为验证本文方法的实用性，以QPZZ-Ⅱ旋转机械故障实验台为操作平台，选用轴承型号为NU205EM，对轴承外圈故障信号进行分析,实验台及故障轴承外圈如图9所示。该滚动轴承参数如表3所示，信号的采样频率为25 600 Hz，时间10 s，轴承转频变化范围：11.4～24.6 Hz。

图9 QPZZ-Ⅱ旋转机械故障实验台及故障外圈

表3 滚动轴承NU205EM参数

故障振动信号时域波形如图10所示，键相脉冲信号如图11，拟合出的转频曲线如图12。对该故障振动信号做同步压缩小波变换，可得时频图如图13所示，从时频图上可以清晰识别故障信号转频及其倍频变化情况，是一种有效的时频分析手段。从此时频图中提取出转频曲线与实际转频曲线对比，如图14，通过计算得转频曲线估计误差为9.51%，能够满足实际应用需求。

图10 时域波形

图11 键相脉冲

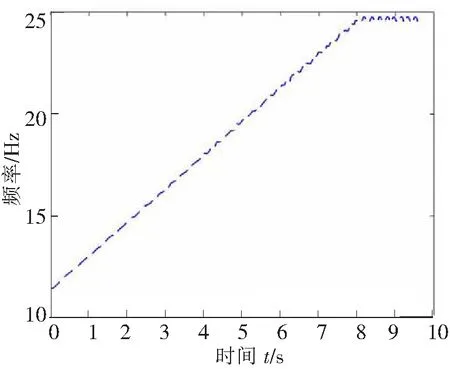
图12 转频曲线

图13 同步压缩小波变换

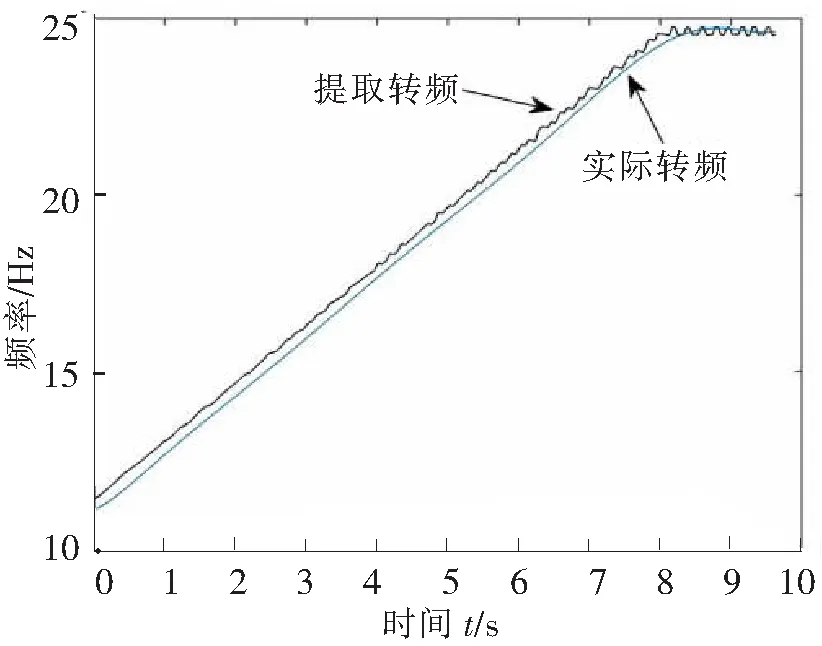
图14 转频曲线对比图

4 结论

通过几种典型信号对STFT、CWT和SST 3种方法对比分析，结果表明SST在时频聚集性上较传统方法STFT和CWT显著提高，且具有较强的噪声鲁棒性，通过实测轴承变转速故障信号验证了其实用性，对于复杂工程信号，SST是一种有效的时频分析方法。