基于博弈论组合赋权的正态云模型在地下水水质评价中的应用

朱志强，唐金平，张 强，彭 琪，李 莹

(1.成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059；2.中国石油天然气股份有限公司浙江油田分公司，杭州 310000)

0 引 言

近年来，随着国家工业化、城镇化进程的加深，地下水的不合理开发现象愈发加重，由此导致地下水污染问题日趋严重，水质情况不容乐观[1]，因此对地下水进行水质分级，建立健全的地下水资源信息系统，对地下水质量保护、地下水资源的合理利用具有重要意义。目前，有很多的水质评价方法，如投影寻踪法、F值法、变异系数权重法、模糊分析法、贝叶斯模型等。上述研究方法对水质分级评价的研究起到了重要的推动作用，但对评价指标的模糊性和随机性等问题上适应性很差，因此探索新的水质评价模型是很有必要的。

正态云模型在模糊集理论的基础上发展而来，融合了模糊性和随机性等特点，李德毅等[2]已经证明了正态云模型的适用性。由于水质分级及影响因素，故将正态云模型引入水质评价中。鉴此，本文采用正态云模型对水质状况进行识别与比较分析，充分反映水质变化趋势；同时采用G2赋权法确定主观权重，CRITIC赋权法确定客观权重，并通过博弈论的组合赋权思想，充分挖掘权重信息，构建基于博弈论组合赋权的正态云地下水水质评价模型。以新疆独山子区周边8组地下水水样为研究对象，根据研究区地下水水质评价特点分别采用模糊综合评价法及基于博弈论组合赋权的正态云模型对其进行评价，并对模型评价结果的可信性进行分析。

1 研究方法

1.1 G2赋权法

G2赋权法是一种更适用于实际应用的区间映射赋权法。相对于其他主观赋权法，G2赋权法的有如下特点：方法灵活、能充分反映专家风险意识、便于推广等，从而能弥补因信息不足，专家或决策者进行主观赋值时无法给出确定数值的缺点[3]。

设某个决策者在待评估水质指标集合{Xj}中挑选出决策者认为重要性最小的指标作为唯一参照指标，记作Yn。将其他水质指标重新排序标记为(Y1，…，Yk，…，Yn-1)。不难看出集合{Xj}与{Yk}是一一对应的。

本次水质数据为点赋值情况，所以采用带有点赋值特征的G2赋权法求取各指标的主观权重。

设指定的决策者根据水质相关信息，判断水质指标的重要性程度之比Rk：

(1)

如Rk赋值准确，则可计算确定水质指标Yk的权重系数：

(2)

1.2 CRITIC赋权法

CRITIC赋权法是一种客观权重确定方法，是由Diakoulaki在1995年提出的，适用于多指标客观权重的处理[4]。该方法中各评价指标的客观权重是通过评价指标内的变异性和评价指标间的冲突性来综合确定。变异性表示同一指标下的取值差异，用标准差的形式来表现，标准差越大则差距越大，表示数据样本所反映的信息量越大。指标间的冲突性通过相关系数来反映，相关系数的大小和正负决定着所占权重的大小。若指标间负相关系数越大，表示冲突性越大，说明指标所反映的信息有很大的差异，故指标所占的权重也越大[5]。

假设待评价的水样个数为m，评价指标个数为n，bij为第i个水样的第j个评价指标的实测值，则待评价的水样实测值矩阵B为：

(1)无量纲处理。为消除数据量纲的影响，需要用公式(3)对实测数据进行无量纲处理，得到处理后的矩阵E。

(3)

(2)计算评价指标内的变异性代表值标准差σj。

(3)计算各指标间的相关系数rij，并根据公式(4)计算评价指标的冲突性代表值Rij。

(4)

(4)根据公式(5)计算Hj。Hj代表的是第j个指标包含的信息量，其值的大小表征评价指标包含信息量的多少及指标的相对重要性。

(5)

(5)根据公式(6)可计算得到权重：

(6)

1.3 基于博弈论组合赋权

基于博弈论的组合赋权法是以纳什均衡为协调手段，寻求主、客观权重冲突内的一致和妥协，是一个比较与协调相集成的过程，并寻找两者之间共同利益的最大化。该方法能综合主、客观权重的优点，全方位地考虑各个指标间的固有信息，降低主观随意性进而提高指标赋权的科学合理性。组合赋权步骤如下[6]：

(1)本文依次采用主、客观赋权方法计算水质指标权重，基本权重向量集为uk={uk1，uk2，…，ukn}，(k=1,2，…，n)，水质评价指标个数为n，指标赋权方法个数为L，本文L为2。设线性组合权重系数α={α1，α2，…，αL}。这些向量任意线性组合为：

(7)

(2)寻求不同权重之间的一致与妥协，以u和uk的离差极小化为目标，优化式(8)中L个线性权重组合系数αk，得到u中最满意的权重，从而目标函数为：

(8)

(9)

1.4 正态云模型

云模型是以正态分布和钟型隶属函数为基础的数学模型，用于实现客观世界中某事物和现象定性与定量之间发生不确定性转换，对于水质评价过程中的随机性、模糊性和离散性问题有很好的适用性[7-11]。模型利用期望Ex、熵En、超熵He有机地将水质评价中的随机性、模糊性和离散性结合起来，进而通过语言值完成定性与定量之间的不确定性转换[12]。

(1)水质评价的正态云模型生成步骤如下：

①以云特征参数Ex、He2为期望和标准差，生成正态随机数En′；

②以云特征参数Ex为期望、正态随机数En′为标准差，生成正态随机数x；

④循环上述步骤，生成足够多的云滴，本文生成3 000个云滴。

(2)水质评价正态云模型的云特征参数计算步骤如下：Ex为水质分级综合评价指标的期望，由下式给出：

(10)

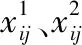
En为云模型的熵，由公式(11)给出：

(11)

超熵He=k，其中k为常数，反映云模型的离散程度。

依照上述方法可计算得到水质评价云模型的特征参数(见表1)。

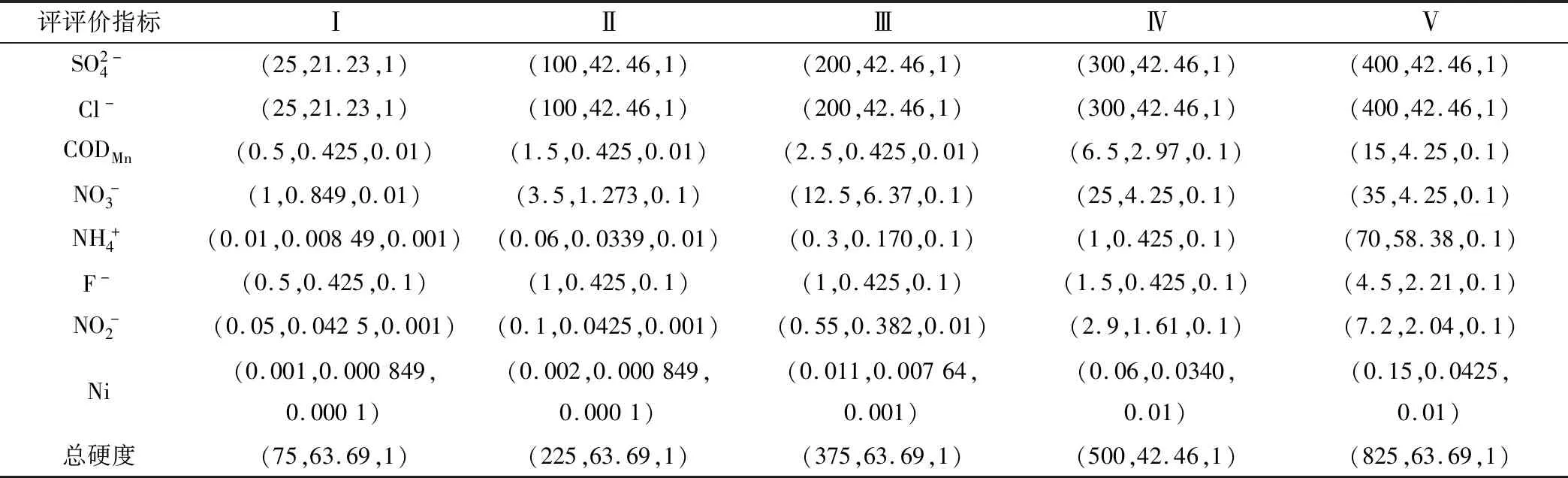
表1 正态云模型特征参数(Ex、En、He)Tab.1 Normal cloud model characteristic parameters(Ex、En、He)

2 实例应用

表2 2015年独山子区地下水水质监测数据 mg/L

根据本文上述的博弈论组合赋权方法计算步骤，分别将G2赋权法、CRITIC赋权法及基于博弈论的组合赋权法所得的9个指标权重进行对比(表3)，并引入相对熵[8]理论。

(12)

上式为P、Q的相对熵。相对熵值越趋近于0，则组合权重与不同赋权法所得权重差异越小、一致性越好。经计算，组合赋权法与G2赋权法的相对熵为0.010，与CRITIC赋权法相对熵为0.007，可得知组合赋权法与这两种赋权法的一致性程度较好，所得权重具有合理性、科学性。

表3 各种权重计算方法结果比较Tab.3 Comparison of results of various weight calculation methods

得到水质评价指标的隶属度矩阵，结合表3中的组合权重矩阵，即可得到水样的水质评价结果。为了验证本文方法的可行性，选取模糊综合评价法进行对比分析。水质综合评价结果见表5。

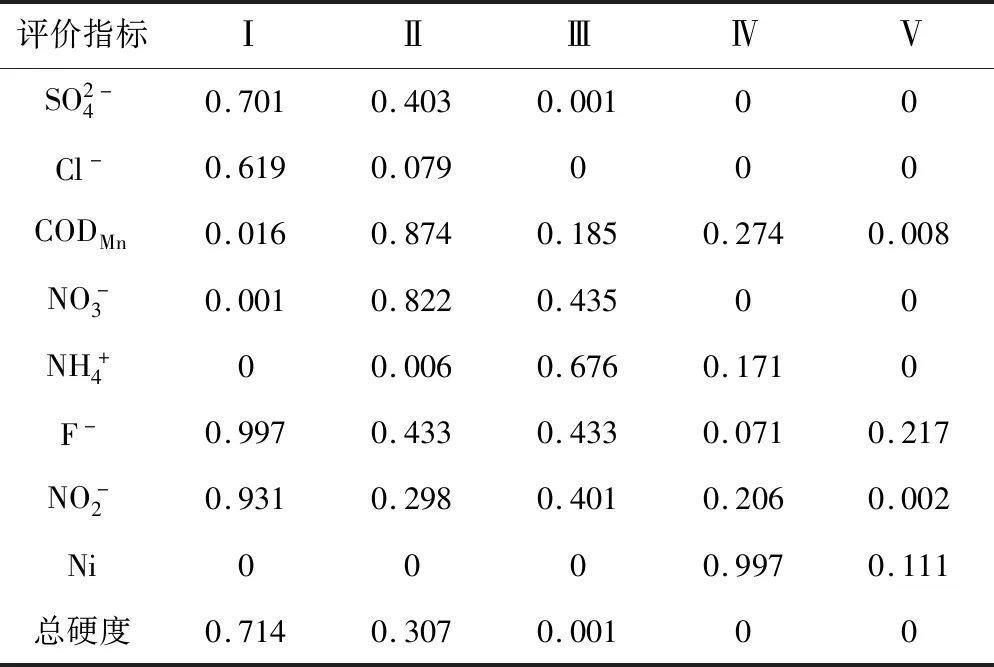
表4 Z01水样评价指标的隶属度Tab.4 Membership of Z01 water sample evaluation index

表5 水质评价综合结果Tab.5 Comprehensive results of water quality assessment

对比分别基于博弈论组合赋权、CRITIC赋权及G2赋权的正态云模型评价结果，Z07水样的CRITIC赋权与博弈论组合赋权评价结果存在差异，进一步分析得到基于CRITIC赋权法的评价结果过于客观，而博弈论组合赋权法结果更为准确，更贴近于现场水质情况；G2赋权和博弈论组合赋权评价结果一致，考虑为水样数据量的限制导致的偶然性，可进一步验证讨论；博弈论组合赋权法兼顾了主、客观优势，解释性好。模糊综合评价法应用三种赋权方法所得评价结果进行对比，同样存在类似情况，G2赋权法过于强调主观信息，使Z04评价结果有偏差。

对比基于博弈论组合赋权的正态云模型、模糊综合评价模型，一致率达75%，其中Z03、Z08水样的水质评价结果有区别。结合Z03水样的水质监测数据及环境基底值，Z03水样的水质更趋于IV类，而模糊综合评价法评价结果为I类水，进一步分析其原因为模糊综合评价法忽略了评价因子之间的联系，导致评价结果偏离事实；Z08水样的水质评价结果存在差异，同样是因为模糊综合评价法忽略了评价因子之间的联系，使得评价结果偏好，从而偏离事实。

不同的水质评价方法在同一组水质指标下获得的评价结果往往存在差异性，总体来看，基于博弈论组合赋权的正态云模型评价结果相对模糊综合评价法更有可信性。采用博弈论组合赋权法，通过综合两种赋权方法确定指标权重，能够将两种独立的赋权方法融合起来，既避免决策者的意愿偏好，又考虑了各指标之间相互作用的隐含信息。此外，基于博弈论组合赋权的正态云模型加强了评价因子间的联系，使得评价结果更具科学性、真实性，其计算方式更为简单、快捷，值得进一步开展多样本的对比研究。

3 结 论

(1)相对于传统的评价方法，采用正态云模型，经过3 000次运算，取平均值为评价结果，更具有真实性。并且易于计算机程序实现，使得计算过程简化，大大提高运算效率，降低运算成本。

(2)引入博弈论组合赋权思想，综合两种赋权方法优点，避免了决策者的主观偏好，并充分挖掘了指标隐含的信息量。使组合所得指标权重更具有科学性、合理性。

(3)使用Kullback相对熵理论，认为组合权重值与其他两种赋权方法所得权重值是独立离散分布的，验证了三者之间一致性，证明了博弈论组合赋权结果的真实性。

(4)基于博弈论组合赋权的正态云模型，对新疆独山子区8组水样进行了水质分析与评价。实例结果显示，该区域水质多呈Ⅰ、Ⅱ类，局部水质出Ⅳ类，水质变化相对稳定。