基于集合经验模态分解方法的上证综指波动特征分析及预测研究

刘佳祺　刘雨岚　沈雨霏　刘德红

摘要：股票市场的价格具有非平稳的非线性特征，因此直接预测非常困难。在本文中，我们使用集合经验模式分解方法将上证综合指数的时间序列分解为有限数量的IMF函数和一个趋势项。然后对IMF进行重构得到高频序列、低频序列、长期趋势三个部分，再将得到的三个部分分别输入BP神经网络进行训练得到三个预测值，最后，整合三个预测值以获得最终预测值。实证结果表明，EEMD-BP方法比传统的股价预测方法具有更高的预测精度。

关键词：上证综指;股指预测;集合经验模态分解模型;BP神经网络

中图分类号：F830.91

文献识别码：A

文章编号：1001-828X（2019）010-0319-03

一、引言

股票市场是一个国家宏观经济运行的“晴雨表”，在金融市场的发展中占有重要地位。因此，研究股票市场波动特征和股指预测具有重要意义。目前股票指数预测的方法主要可以分为三类：证券分析法，时间序列法和人工智能法。已有文献表明，人工智能法中的BP神经网络模型被广泛应用于投资预测领域，具有很强的应用价值。但是如果直接将股票指数等原始数据作为参数输入到神经网络中，干扰项比较多，导致信号的特征量并不突出，神经网络需要很长的时间才能把握信号的特征。因此，作者采用Huang等提出的EEMD算法，将原始序列分解后得到的固有模态函数输入BP神经网络，大大提高了BP神经网络的学习训练的效率。综上所述，本文采用EEMD方法和BP神经网络模型相结合的方法来预测上证综合指数，选取2013年1月4日至2018年12月28日上证综指每日收盘价作为原始数据，实证结果表明EEMD-BP模型的方法是有效的。

二、研究方法

1.集成经验模态分解法（EEMD）

经验模态分解法是由Wang等在1998年提出的，其基本原理是将复杂信号分解成若干个相互独立且正交的本征模态函数（IMF），能有效地处理非线性信号。但是研究表明，在存在较多的噪声干扰时，EMD方法经常会出现模式混叠的情况，不能将IMF从原始序列中完全分离出来。为了解决这个问题，2004年Wu和Huang在EMD的基础上提出了集成经验模态分解算法（EEMD）。其基本原理是在原始信号中加入一组白噪声，再对增加了白噪声的信号进行EMD分解，然后重复以上步骤。因为白噪声的功率谱密度在整个频域内是个常数，我们可以认为白噪声均匀分布在整个频域中。当每次选取的白噪声密度不一样时，就会分解得到不同的一组IMF值。把所有得到的IMF值取平均值作为最终结果，既可以消除白噪声的影响，也解决了模式混叠的问题。

假设原始数据为x（t），EEMD算法具体步骤如下：

步骤一：将白噪声加入原始信号中，得到含有白噪声的原始数据x（t）

步骤二：用三次样条函数把x（t）的局部极大值和局部极小值分别连接起来，构成x（t）的上包络线u（t）和下包络线l（t）

步骤三：计算x（t）的平均包络线

公式

步骤四：用x（t）减去m1（t）得到h1（t），若h1（t）满足：1）极值点个数和零点数相差不超过1;2）在任意时刻上下包络线的均值时0，那么h1（t）就是一个IMF分量。

步骤五：若h1（t）不满足以上两个条件，则将h1（t）作为新的原始序列，重复以上四个步骤，直到得到的序列满足IMF的两条性质为止，将该IMF称为c1

步骤六：用原始数据x（t）减去第一个IMF分量c1得到差值序列r1（t）：r1（t）=x（t）-c1，将r1（t）作为原始序列并重复以上几个步骤直至提取出所有IMF为止，此时rn（t）只有一个极值点或变成一个单调函数。因此，原始序列x（t）可以写成：

公式

，其中n为IMF的个数，ci为各IMF分量，rn（t）为残差项

步骤七：分别对原始信号加入不同的白噪声，重复步骤二到六;

步骤八：将得到的IMF集成均值作为最终的输出结果。

由于加入的白噪声是均匀分布在频域空间中的，均值为0，能自动消除模式混叠问题，得到的结果也更加接近真实值。根据Wu和Huang的建议，白噪声序列的次数可以根据公式

公式

得到，其中εn为最终误差的标准差，ε为加入白噪声的标准差，N为集成次数。一般情况下，将白噪声序列的标准差设为0.1或0.2即可，集成数量设为100次。

2.BP神经网络算法

BP神經网络是目前应用最广泛的前向反馈网络，与反馈神经网络不同，前馈神经网络的各神经元只接受前一层的数据输入并输出给下一层，并不反馈回上层，具有很强的非线性映射能力，预测精确度较高。BP神经网络全称为Error Back Propagation，即利用给定输入值与期望输出值之间的误差的反向传导原理，反向从输出层到输入层对网络各层的权值（均值）和阈值（临界值）不断修正，直到网络输出的误差最接近预期值为止。具体步骤为：首先拟定初始化的三层权值及阈值，将训练样本的原始数据输入输入层中，输入层正向将参数传递给隐含层，隐含层利用未完全训练的模式计算出输出参数，再将输出参数传递给输出层输出。随后计算上述步骤输出结果与预期结果的误差，并反向传递，先修正输出层的权值及阈值，反向传播到隐含层，修正隐含层的权值及阈值。至此一次训练结束，开始第二次训练，直至网络输出的误差达到预期值为止。

3.EEMD-BP模型

集合经验模态分解法在非对线性、非平稳序列的处理方面具有很强的优势，而BP神经网络则在预测方面具有很高的精确度，因此将二者结合是一种很好的方法。用EEMD-BP模型预测上证综指的流程图如图1所示，首先用集合经验模态分解法分解上证综指时间序列，得到一组有限个固有模态函数（IMFi）和一个趋势项（R），然后对固有模态函数进行重构，按照频率将新的IMF分成高频序列和低频序列，再加上趋势项代表的长期趋势共三个时间序列，分别输入BP神经网络进行重复训练，得到三个预测值，最后将三个预测值进行整合得到最终预测值。

三、实证研究

1.数据来源及说明

本文的实证研究选取了2013年1月4日至2018年12月28日上证综合指数的收盘价作为样本数据，共1458条数据。数据来源：网易财经

2.上证综指的EEMD分解

（1）EEMD分解

本文利用MATLAB软件对1458条上证指数收盘价数据进行分解，将白噪声设置为0.1倍标准差，总体平均次数设定为100次。经过EEMD分解之后得到9个固有模态函数和1个余项，如图2所示。这九个分量的主要区别是波动频率的不同，IMF1是原始数据最先分离出来的变量，频率最高，IMF9是原始数据最后分离出的变量，频率最低，R是分离出所有IMF函数后的余项，可以很好地反映出原始数据的趋势。从图中我们可以看出，上证综指在这在这五年中是先增后减的。

我们对每个IMF分量和残差项做统计分析可得表1，其中的Pearson系数是指固有模态函数IMF和趋势项R与原始未分解序列的相关性，而方差占原始序列比例反映了分解后的各IMF函数对原始序列波动的贡献率。由表可见，随着频率的增大，IMF的周期也变长，IMF与原始序列的相关性和对原始序列波动的贡献都呈现增长的趋势。

（2）IMF的重构

我们采用均值为0的T检验的方法对得到的IMF分量进行重构。由表2可知，在10%的显著水平下，IMF1-IMF5在零均值检验原假设是不显著的，从IMF6开始均值发生显著变化。由于EEMD分解之后的每个IMF分量都是相互独立的，因此我们可以把IMF1到IMF5相加，得到高频序列，再把IMF6到IMF9相加，得到低频序列。

对重构后得到的高频序列、低频序列和余项分别进行相关性分析，由表3可见，低频序列和趋势项R与原始数据的相关性较大，分别为0.8960和0.6583，而高频序列与原始序列的相关性仅为0.3439，方差占原始序列比例仅为7%，这说明原始序列的波动主要来源于低频序列。

（3）波动特征分析

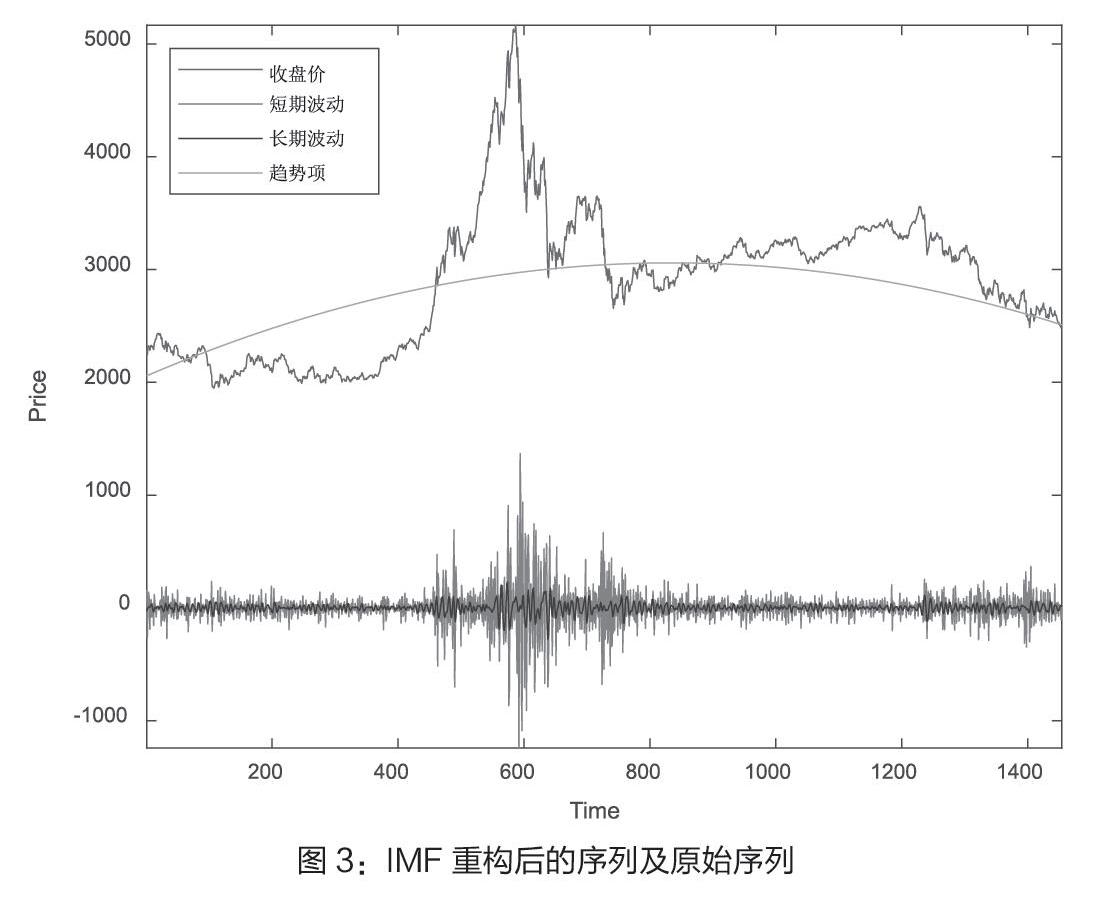
经IMF重构后的序列和原始序列如图3所示，由图中可以看出，高频序列始终在零点附近随机波动，代表了股票市场中正常波动;低频序列则是在零点附近上下振动，表示重大事件对股票市场的影响;趋势项则反映了股票市场的长期变化趋势。

3.上证综指的短期预测

本文用EEMD模型分解后得到的高频序列、低频序列和趋势项作为BP神经网络的输入层，神经网络的输出层为上证综指的预测价格。当增加足够多的神经元节点时，神经网络的单个隐含层总能实现从输入层到输出层的任意非线性映射，所以即使面对股指这样的复杂情况，只要经过足够多次的训练，一个隐含层即可满足大多数情况。因此本文选择只一个隐含层的三层BP神经网络，隐含层节点的个数则根据沈玉花等提出的BP神经网络隐含层单元数改进方法确定。

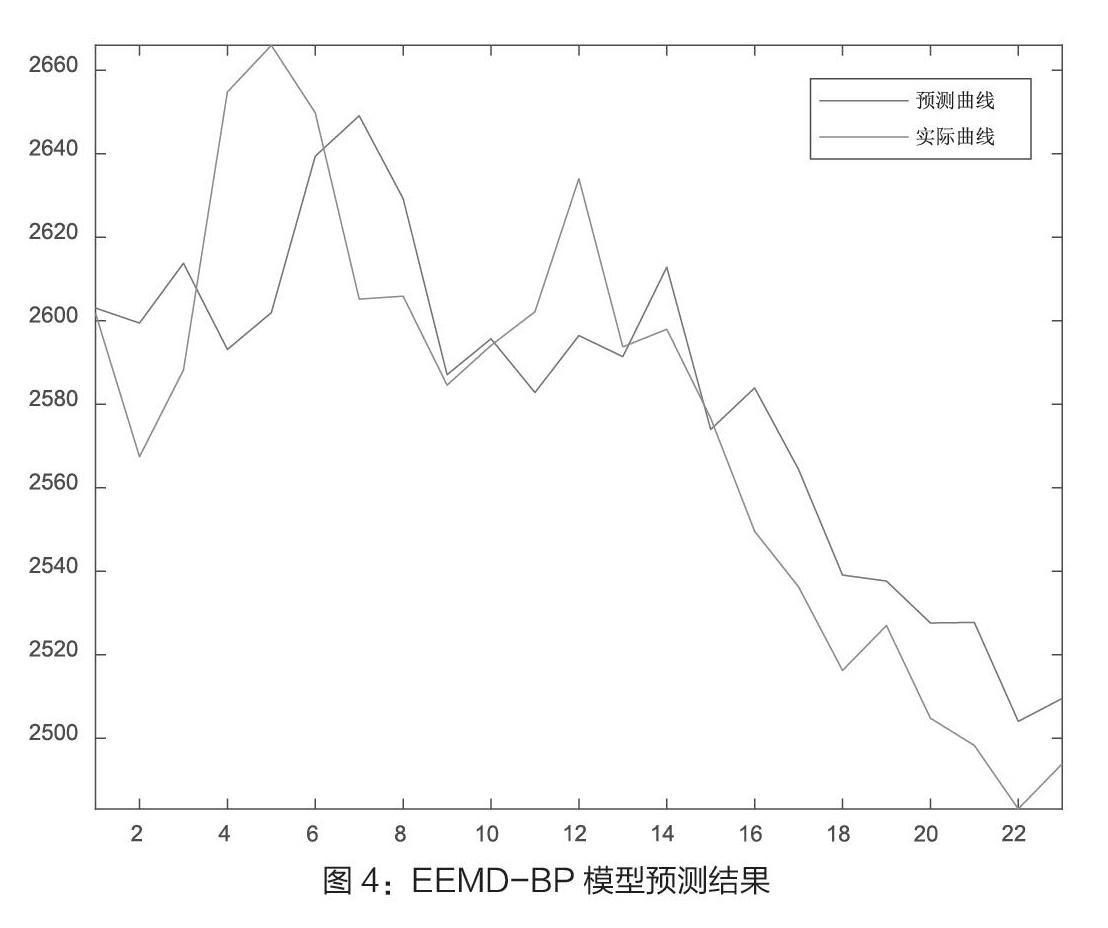
网络结构确定后我们需要对BP神经网络模型进行训练，将前1436组数据作为训练样本训练神经网络模型，并用后22组数据作为预测样本，选取输入层节点数为4，然后根据前文所述选取隐含层节点数的方法确定最佳隐含层节点数为2，再将所得的高频、低频序列和余项的预测值进行整合得到最终预测结果，如图4所示。

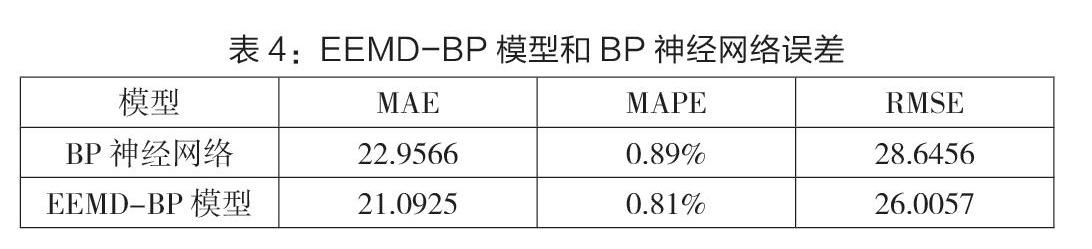
为了验证EEMD-BP模型的有效性，我们用BP神经网络模型对原始数据进行预测作为对比，两个模型的误差如表4所示。本文采用平均绝对百分比误差（MAPE）、平均绝对误差（MSE）和均方根误差（RMSE）来衡量两个模型的误差，数字越小越好。由表中可以看出，EEMD-BP方法准确度明显高于单独采用BP神经网络预测的值，这说明的EEMD模型能提高预测的准确度。

四、结语

本文通过采用EEMD和BP网络模型结合的方法对上证综指的价格进行研究，得到以下两个结论：一是EEMD模型能有效地处理非线性序列，把握原始序列信号特征，有助于BP神经网络的训练过程;二是先利用EEMD模型对数据进行平稳化处理，能提高BP神经网络预测的准确度，减小预测结果与实际结果之间的误差。

参考文献：

[1]何凯，苏梽芳，何卫平.上证基金指数波动结构分解与短期预测：基于EEMD模型[J].金融理论与实践，2014（1）：80-85.

[2]阮连法，包洪洁.基于经验模态分解的房价周期波动实证分析[J].中国管理科学，2012，20（3）：41-46.

[3]刘海飞，李心丹.基于EMD方法的股票价格预测[J].统计与决策，2011（10）：59-61.

[4]陈园园，刘俊，傅強.基于EMD的神经网络股价预测方法[J].新疆大学学报：哲学·人文社会科学版，2014，42（4）：6-11.

[5]王文波，费浦生，羿旭明.基于EMD与神经网络的中国股票市场预测[J].系统工程理论与实践，2010，30（6）：1027-1033.

[6]秦宇.应用经验模态分解的上海股票市场价格趋势分解及周期性分析[J].中国管理科学，2008，16（S1）：219-225.