一种重力流出给料槽的测试及分析

曾艺宾

（漳州佳龙科技股份有限公司，福建 漳州 363000）

固体颗粒流动性属于粉体工程的研究领域，而粉体工程则是一门新兴的综合性科学技术，在国际上以二十世纪四十年代的《Micromeritics》的发表为研究起点。六七十年代由于能源、化工、采矿等行业的飞速发展，粉体工程得到进一步的发展，而在八十年代，粉体工程多研究超细颗粒，九十年代则进一步发展到纳米技术，进入原子、分子级的研究时代。美国、德国、日本等发达国家均有多所大学及相关研究机构进行粉体工程的相关科研，但是国内粉体工程的研究还相对落后，资料及成果都较少，研究多集中在采矿、化工等相关领域，粮食行业方面对粉体工程的研究则多在仓储及气体输送方面。

由于粮食行业涉及的相关颗粒物料，特别是大米具有良好的流动性，所以从十九世纪后期，固体颗粒自动定量设备出现以来，国内外多采用结构简单可靠的重力流出给料方式，到二十一世纪，已经普及应用到全国各地。但是对这种给料方式的研究和改进，多集中在机械结构及尺寸的优化上，对于物料在给料机构槽体内的实际流动情况，影响流速变化和流速误差的各种因素，相关资料很少，尚未明确因素较多；并且，研究给料槽体内部物料的实际流动情况较少。因此，为了提高重力流出给料方式的给料性能，必须进一步研究相关的各项参数对于固体颗粒流速及误差的影响，分析现有给料槽体结构设计的合理性，从而为改进给料机构提供理论及数据基础。

1 大米的特性分析

根据《粮食工程设计手册》[1]，大米堆密度ρ=0.8 t/m3，内摩擦角为30°；与钢板外摩擦角为23°；粒度为7 mm×3 mm×2.5 mm。根据Geldartr的4类型颗粒理论[2]，大米属于D类颗粒，颗径远大于0.5 mm的分界值，具有重力作用强[3]、负压梯度影响小[4]的特点。查卡尔流动指数表[5]，可知大米属于流动性最好的颗粒，流动指数在90以上，均匀性系数达到23左右，压缩率低于10%，一般不必要做架桥防止措施。

2 影响大米重力流出的主要因素

颗粒物料分别具有固体及流体的部分特性[2]，由于重力作用会在给料槽中发生滚动、滑动及沉降等动作，流动规格复杂多变，流速大小及误差都难以控制。流出的不稳定主要体现在以下几点：

⑴ 流速不稳定，时快时慢。

⑵“结拱架桥现象”物料忽然停止卸出。

⑶“中心流现象”只有料仓出口上方的物料流出，四周物料不动。

⑷“虹吸现象”底部物料拉动仓物料不断卸出。

⑸ 偏析现象，不同性质颗粒不能同步流动，出现分层。

由于大米自身物理特性，流出不稳定现象主要是⑴、⑵、⑶三种，而⑷、⑸的现象很少出现。

流动形式[5]对流速大小影响较大：颗粒从给料槽内流出分为2种基本形式，即整体流和中心流（漏斗流）。其中整体流流速快且稳定，可以实现先进先出原则，是设计给料槽的理想流形；而漏斗流则流速慢且不稳定，而且容易出现残料等问题，是设计给料槽必须避免的流动形式。

有研究[3]指出在粗颗粒中混合入细颗粒，在一定程度上能加大流速，但是如果混入太多，反而会减小流速。考虑到碎米在大米内的占比按国家标准GB/T 1354的要求最高为35%，其中小碎最高2.5%，所以可以判断碎米将对大米流速产生加大流速的影响。

随着物料从给料槽流出，在出口特定区域会发生负压现象[2]，该现象会减慢物料的下落速度，一定程度上减小流速，这个现象在物料颗粒小（特别是粉状物料）的情况下影响较大，但对于颗粒较大的大米，该现象可以忽略不计。

物料的内摩擦角越大流速越小[6]，堆积密度越大流速越大，因为本次研究的物料大米，以及扩展到其它物料如薏米、红豆等物料，都属于颗粒较大、流动性较好的物料，内摩擦角在流型预测上有所应用，而堆积密度则可以直接体现在流速的质量监测上面。

而贾力伟[7]等人则通过研究发现，常用粉体壁面摩擦角对流速还是产生了一定的影响，所以粉体内摩擦角如果与壁面摩擦角相差越大，颗粒体积越大，料仓直径与半锥角越小，壁面摩擦角影响会越大。

粮仓效应[7]是比较公认和成熟的理论，垂直方向上的压力随着高度变化会进入饱和区，料位高度超过仓体直径2倍后，料位高度增加压力将不再增加。原理是颗粒的相互作用将压力分散到仓体侧壁，不再影响到仓底。锥形仓也有同样的效应，料位高度超过一定界限，对流速不再有影响。按《粉体技术手册》的介绍[8]，料位高度超过4倍出口直径，不再影响出料流速。

3 给料料槽形状对重力流出的理论分析

考虑到结构设计及加工的简易性，传统给料槽水平截面多以矩形为主，竖直侧截面以楔形为主，配合弧形自重式闸门实现开合动作。实现动作的机械结构[11]如图1。

如图1，槽体1固定不动，闸门5在气缸2的驱动下可以绕着转轴4做旋转动作实现闸门开合，而限位杆3则可以在电机带动下调整角度，用于限制闸门开口尺寸。

图1 一种无极调节的给料闸门开合机构

3.1 给料槽体形状分析

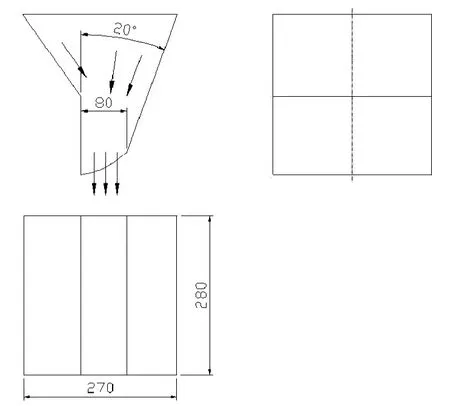
图2 一种典型的重力流出给料槽体形状

如图2所示为一种现有的重力流出方式给料槽形状，它的出口形状为80 mm×280 mm的矩形，符合在相同半锥角的情况下，圆形仓流速最差，方形好一些，矩形仓最好，矩形的长边要大于短边3倍以上[9]的设计要求。该形状最有利于增加流速。

Harmens等人实验[6]证明了料仓仓体直径大于1.3倍料仓出口直径后，料仓直径对流速影响就很小。本槽体入口面积为270 mm×280 mm=75600 mm2，出口面积为80 mm×280 mm=22400 mm2，比值为75600÷22400=3.375＞1.3，出口面积符合要求。

给料槽竖直的侧截面，由于两边半锥角不同形成的不同形状料仓会影响流速[8]，单边竖直的楔形结构最有利于物料的重力流出。图中的半锥角为20°，查流动形式判断图[5]，可以预判流动形式为整体流。

3.2 闸门与给料槽配合分析

图3 闸门与给料槽配合结构简图

如图3所示，闸门为弧形闸门，闸门边缘与给料槽出口左边缘形成宽度尺寸W，闸门可绕着A点转动，所以宽度尺寸W可控制在0～80 mm的范围内；槽长尺寸不可调整，为固定数值280 mm，槽宽与尺寸W共同组成矩形的落料开口。

闸门在转动过程中，除了尺寸W，随着发生变化的还是角度β，在尺寸W较小的时候，角度β可粗略视为半锥角，但随着尺寸W的增加，给料槽20°的半锥角起的作用将越来越大；测量可得角度β的变化范围在46.4～69.8°之间，基本上大于理论计算公式里的45°的临界角，所以角度β的变化对质量流速的影响不大。因此，随着开口宽度W值的变化，质量流速M值能相应稳定变化。但是由于结拱临界条件的存在，当W值小于一定数值后，质量流速会变得不稳定，流速误差会变大。

4 测试数据统计、计算及分析

4.1 测试条件简介

实验设备由提升机构、给料机构、计量机构及电控部分组成，采用全自动循环连续测试，电脑自动数据采集。提升机构主要由斗式提升机、下缓冲仓、上储料仓构成，主要用于将测试过的物料由计量机构放料至下缓冲仓，再提升至上储料仓，给上储料仓下方的给料机构供料，实现测试循环。计量机构由悬挂在3个电子应变式波纹管传感器下方的带有气动V型闸门的计量筒构成，用于重量信号采集以及自动卸料清零。给料机构是主要测试对象，采用气动方式自动实现快加及慢加动作，并可以利用电机调整快加开口大小。电控部分以触摸屏为操作界面，仪表作为秤重控制核心，利用传感器进行重量采集，采用可编程控制器进行各部件通讯及动作控制，利用无线通讯技术与办公室的计算机通讯进行数据采集，系统分度值1 g。

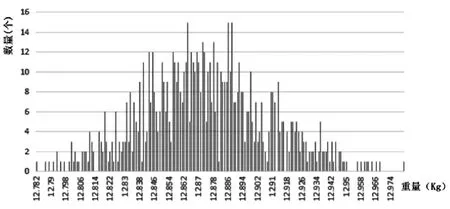
图4 流速误差统计

实验采用循环测试，设定固定目标值后，计量筒卸料后闭合，电控系统回归零点，加料闸门打开，电控系统不断采集计量筒内重量信号，到达目标值后，加料闸门关闭，系统采集重量后，计量筒放料门打开，卸料后闭合，依此循环。由于流速误差的原因，每次采集到的重量数值不同，测试达到一定次数之后，可得到流速误差的正态分布曲线，体现流速误差大小。

4.2 测试结果分析

4.2.1 单组测试数据处理方法

首先对测试所得数据按不同包装重量进行分组，统计每个重量的数量，可得图4。

从图4中可以看出重量分布符合正态分布，测试结果可以在一定程度体现流速误差的范围。用最大包装重量减去最小包装重量可得误差范围，累计所有包装重量及包装时间相除可得质量流速，每组测试数据均照此处理方法。

4.2.2 开口宽度对质量速率及误差率的影响

如图3所示，闸门改变开口宽度尺寸W的数值，槽长280 mm为固定数值，因此W值的变化能体现开口面积的变化。

按上文所述方法分组测试并处理数据可得表1。

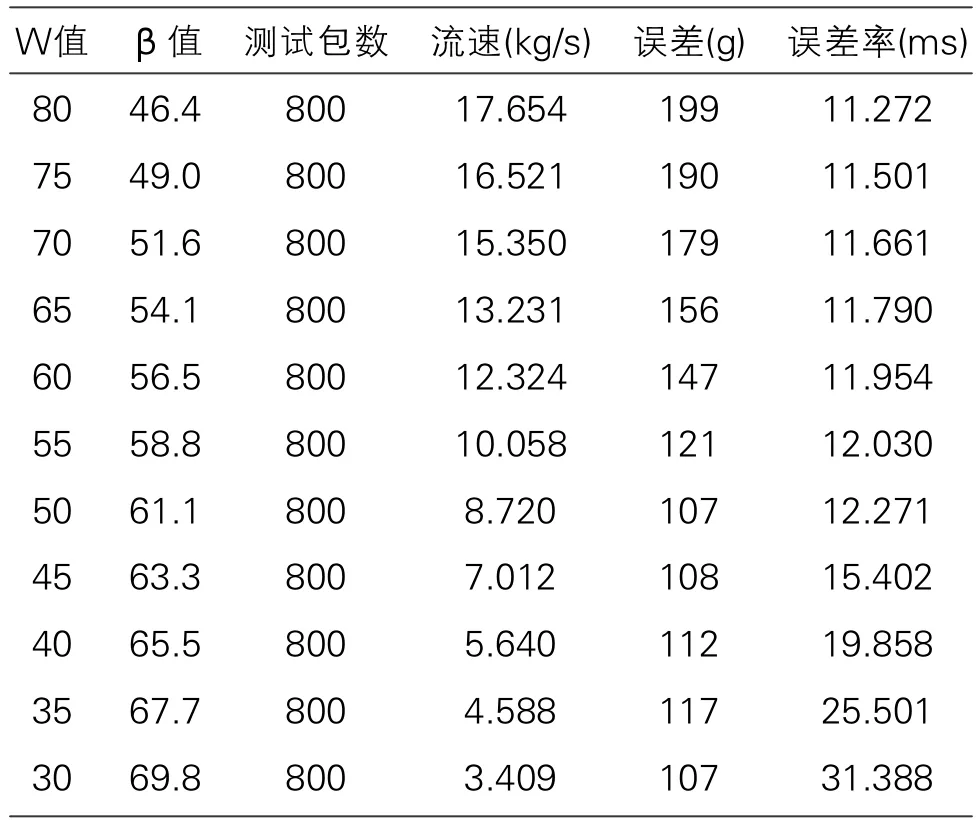
表1 开口宽度与误差率关系表

误差率为误差除以流速，以表示单位流速下的误差大小，作为流速稳定性的量化指标。

以上，我们从小组合作学习之于初中数学教学活动的意义入手，对初中数学课堂上如何开展小组合作学习进行了思考与探究。新课程标准背景下，初中数学的教学模式和教学手段都得到了一定程度的丰富。但是要想真正取得效果，实现初中数学教学的有效性，还需要教师更多地根据学生学情以及学生发展规律来制订教学计划，完善教学方法。

将开口宽度W值与误差率关系列为图表，可得图5。

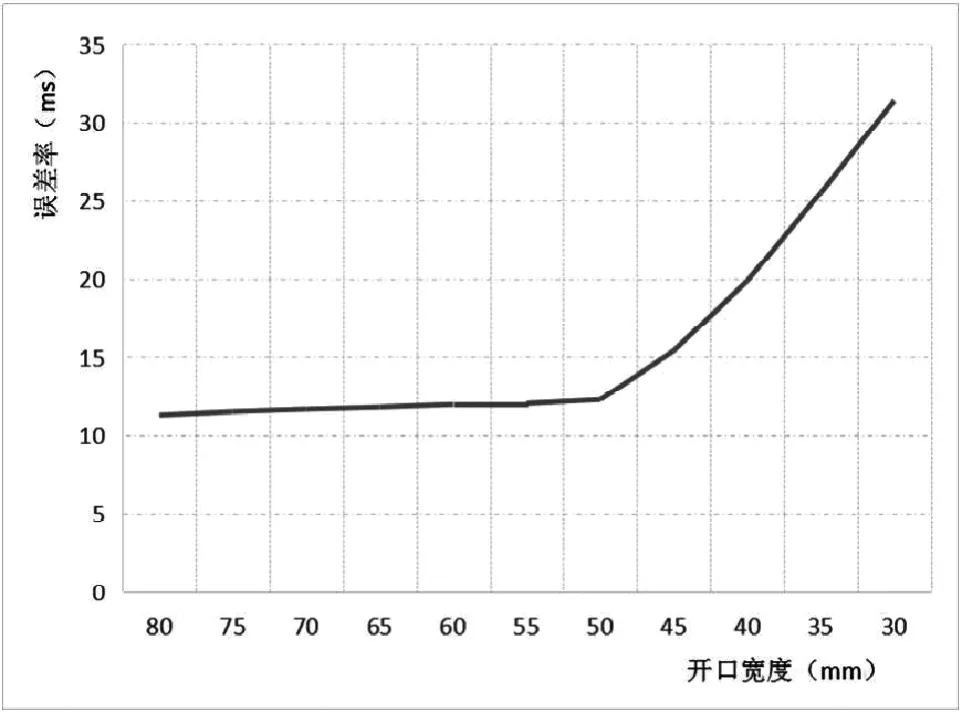
图5 开口宽度与误差率关系图

从图5可以明显看出，在开口宽度W值为80～50 mm之间时，误差率基本上没有明显变化，而在开口宽度W值小于50 mm以后，随着其数值变小，误差率忽然快速变大，可见此时质量流速变得更不稳定。考虑到结拱临界条件的影响[7]，理想的流动开口尺寸为48 mm，符合上文中对给料槽结构的分析结果，也符合实际测试结果。

4.2.3 重力流出质量流速的理论计算与测试结果的对比分析

为了方便与测试结果进行对比，先用经验公式[10]对重力流出的质量流速进行理论计算。

对于矩形出料口的质量流速公式为：

式中：

M—质量流速，即出料口物料通过能力，kg/s；

ρ—物料的堆密度，kg/m3；

g—重力加速度，m/s2；

fp—物料的形状修正系数，球形颗粒该值取1.6，非球形颗粒约为2.4；

d—颗粒直径，mm；

fh—半锥角修正系数，fh=tgβ-0.55，β为半锥角（给料槽中心线与槽壁的夹角），当β＜45°时，β按槽体休止角计算，当β≥45°时，fh=1.0；

L—给料槽出料口长度，mm；

W—给料槽出料口宽度，mm。

大米堆密度ρ=0.8 t/m3；内摩擦角为30°，与钢板外摩擦角23°；由表1可知，测试时给料槽半锥角β均大于45°，因此fh=1.0；大米粒度为7 mm×3 mm×2.5 mm，因此fp≈2.4。

根据上述给料槽结构，以L=200 mm、W=25～90 mm、d=2.5 mm、g=9.8 m/s2为例，将以上数据代入矩形出料口M值计算公式，由于测试进料槽与经验公式推导用进料槽结构与尺寸上的差异，需要根据实际测试数据加入修正系数，得到理论计算数据与修正数据，通过软件进行图表化，再加入表1内所示质量流速M与开口宽度W的测试结果得图6。

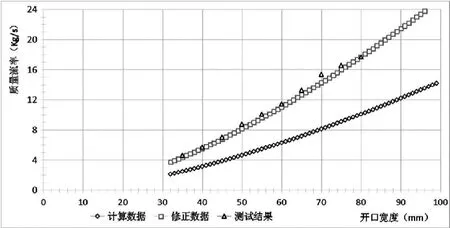
图6 开口宽度与质量流速关系图

由图6可以看出测试结果与理论计算修正后的曲线基本重合，并符合上文的分析结果。当开口宽度W值在30～80 mm时，质量流速M值平稳随着W值成指数变化，并未象误差率一样在W值为50 mm左右发生突变，这证明了误差率受结拱临界条件的影响比质量流速大很多，流速与误差率并不完全同步。

5 结语

本文分析了典型颗粒物料——大米的相关特性，以及影响其重力流出的主要因素，明确了对流速及误差的主要影响因素为给料槽形状、碎米含量、壁面摩擦角（半锥角）等。同时，本文对一种给料槽进行理论分析及实际测试，证实了其形状尺寸的合理性。文章还测试并分析了给料槽闸门逐步关闭过程中的流速及误差的变化情况，发现在这过程中，闸门开口存在一个临界值，当其不断减少并超过该临界值以后，虽然对流速变化影响不大，但会导致误差率快速增大，使料流变得不稳定。