基于RFPA的砾石对砂砾岩破裂影响规律研究

孙元伟，郝勇超，彭国威，王艳丽，董书鑫，程远方，时 贤

（1.中国石油大学胜利学院油气工程学院，山东东营257061；2.中国石油大学（华东）石油工程学院，山东青岛266580）

渤海湾盆地按油气藏类型的统计表明，除构造以外的非构造油气藏探明储量总计约达31×108t，占总探明储量的近40%，其中砂砾岩体油藏探明约6×108t，占7.63%。砂砾岩油气藏一般具有埋藏深、孔隙结构复杂等特点，其储层测井评价、地质工程应用在国内外石油勘探领域均属难题[1-2]，需要新的理论和先进的工程技术来支撑。

组成砂砾岩的材料或组分按其结构特点大体可分为3类：基质，由细小的砂粒组成，具有一定强度；基质中强度较高的砾石,通常不易破裂，具有强度较低的泥岩等；基质与裂缝之间的界面，可能是极为薄弱的裂缝，也可能是具有一定强度的胶结面[3]。砂砾岩内部分布的各种裂纹、砾石等缺陷在外部载荷作用下导致岩石的宏观变形与破坏表现出明显的不连续性、各向异性等特点。常规的力学理论均将岩石视为各向同性介质[4]，忽视了岩石在载荷加载过程中存在的非均匀性特征，其结论无法解决实际工程中存在的问题[5-6]，基于有限元数值计算方法的岩石破裂全过程分析软件系统，RFPA逐渐成为材料破坏分析方面的重要手段之一[7]。K.N.Gebremicael等[8]采用RFPA分析了大倾角每层开采过程中的顶板变形及破坏规律。王云杰等[9]基于RFPA在单轴加载条件下分别模拟了岩石破坏过程及不同尺寸对岩石破坏的影响。钟波波等[10]应用RFPA研究了裂纹倾角及围压对裂纹扩展模式的影响。陈鹏等[11]采用RFPA研究了岩石尺寸对单轴抗压强度的影响，岩石的变形模量和弹性模量随高径比的增大而呈现非线性减小，且抗压强度逐渐增大。黄兴龙等[12]运用RFPA对滑动形成过程进行了数值模拟研究，考虑岩石非均匀性的影响。确定砂砾岩在工程中所表现的力学行为是岩石力学相关的理论研究和工程施工所关心的根本问题。目前人们对硬岩（如花岗岩、砂岩等）以及部分软岩（如泥岩、页岩等）的力学性质研究已经比较成熟，而砂砾岩中各类砾石发育、非均质性强，兼具软岩和硬岩的特点，对其力学性质的研究及岩石力学模型鲜见报道。

笔者建立单轴压缩实验，模拟砾石力学参数、分布特征及形状对岩石弹性参数及裂纹的萌生、扩展和贯通规律进行研究。由于数值模拟技术的可操作性、对比性强，对同一块岩心可以重复进行实验，根据物理实验得到的参数确定数值模型的输入值，建立砾石尺寸、砾石含量及力学性质规律变化的模型，研究这些因素对砂砾岩力学参数裂纹扩展的影响规律。

1 数值模型构建

1.1 基本原理

RFPA是一个以弹性力学为应力分析工具，以弹性损伤理论及其修正后的Coulomb破坏准则为介质变形和破坏分析模块的真实破裂过程分析系统[13-15]。系统将材料介质模型离散化成由细观基元组成的数值模型，材料介质在细观上是各向同性的弹脆性介质，并引入了适当的细观基元破坏准则和损伤规律，基元的相变临界点采用修正的Coulomb准则[16]。材料介质的裂纹扩展是一个准静态过程，忽略因快速扩展引起的惯性力的影响。

RFPA选取等面积四节点的四边形单位剖分计算模型，单元数量以能足够精确的反映介质的非均匀性及一定数量的矿物和胶结颗粒、空洞等细小缺陷为标准。为描述岩石的非均匀性特点，RFPA方法中假定离散化后的细观基元的力学性质服从某种统计分布规律（如Weibull分布），由此建立细观与宏观介质力学性能的联系。如引入Weibull统计分布函数来描述，即：

式中，α为材料（岩石）介质基元体力学性质参数（弹模、强度、泊松比、自重等）；α0为基元体力学性质参数的平均值；m为分布函数的性质参数，其物理意义反映了材料（岩石）介质的均匀性，定义为材料（岩石）介质的均匀性系数，反映材料的均匀程度；ϕ()α为材料（岩石）基元体力学性质的统计分布密度。

利用计算机对岩石的变形与破裂过程进行数值实验，不仅具有通用性强、方便灵活、可重复性强等特点，而且可以通过数值实验得到许多在常规实验中观测不到的重要信息。

1.2 数值模型及参数

在对模型进行数值模拟分析时，所选用的计算输入参数至关重要，本文使用的RFPA商业软件中，将材料假设成非均匀材料，材料细观力学特性的非均匀分布服从Weibull分布。岩体宏观力学特性与细观力学性质通过均质度系数m密切联系。针对本节研究的实际问题，建立的式样尺寸为0.025 m×0.050 m，并划分为200×400=80 000个有限元网格；破坏准则选用经典的Mohr-Coulomb准则。其次考虑到基质与砾石均质度不同，取基质抗压强度和杨氏模量均质度系数m分别为30和3，砾石抗压强度和杨氏模量均质度系数m分别为60和9。RFPA软件将材料的宏观力学参数转化为细观参数后进行输入，转化函数如式（2）所示：

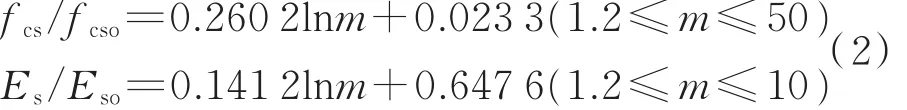
式中，fcs和Es分别为宏观的抗压强度和弹性模量，MPa；fcso和Eso分别为细观按Weibull分布的岩石抗压强度和弹性模量，MPa。基于式（2），大量砂砾岩的室内实验数据与均质度系数m确定模型输入参数（见表1）。

表1 模型的强度参数赋值表Table 1 Model strength parameters

由于数值模拟技术的可操作性、对比性强，对同一块岩心可以重复进行实验，根据物理实验得到的参数确定数值模型的输入值，建立砾石尺寸、砾石含量及力学性质规律变化的模型，研究这些因素对砂砾岩力学参数的影响规律。

通过MTALAB编程建立砾石的随机分布坐标，砾石分布位置不变，简化砾石形状为圆形及不同孔洞尺寸变化的数值模型。应用相同数值模型进行单轴压缩模拟实验，详细探讨了孔洞尺寸的变化对单轴抗压强度、弹性模量、泊松比的影响。设计长50 mm、宽25 mm的标准岩心模型，模型的砾石分布相同、砾石含量为1.6万个/m2、孔径变化在0.4～4 mm的24个理想模型（部分模型见图1），模型的加载条件为位移加载，单步增量为0.000 1 mm。

图1 不同砾石尺寸模型Fig.1 The numerical models of different gravels sizes

2 砾石特征对砂砾岩破裂影响

在建立不同砾石尺寸的标准岩心模型后，首先保持砾石和基质力学参数和分布不变，研究砾石尺寸对裂纹扩展模式及岩心力学参数的影响；然后保持基质力学参数及砾石尺寸、分布不变，仅改变砾石强度，研究其对砂砾岩岩心裂纹扩展规律及宏观力学参数的影响。

2.1 砾石尺寸的影响

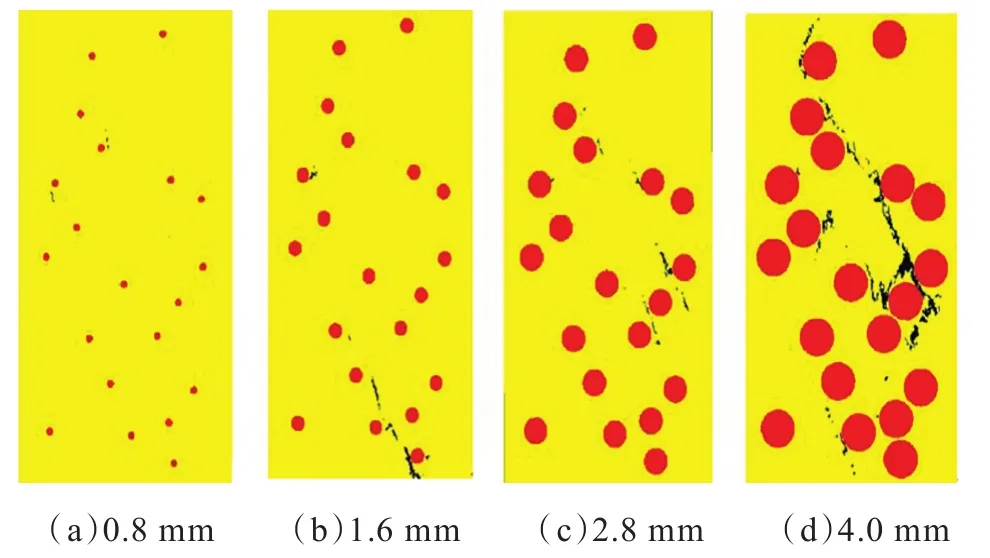
图2 不同孔洞尺寸模型初始破坏图Fig.2 Initial failure diagrams for different gravel size models

对不同砾石尺寸模型进行单轴压缩模拟实验，图2为部分砾石尺寸模型的初始破坏模式。施加轴向载荷，微裂纹最先产生在砾石周围，不同砾石尺寸砂砾岩标准岩心模型的破坏类型皆为剪切破坏。

图3为部分砾石尺寸模型的最终破坏模式。从图3可以发现，轴向位移加载完毕后，随砾石尺寸的增大，生成裂缝越大，破坏越严重；而裂缝产生位置与砾石尺寸无明显相关性，裂纹与砾石成一定角度逐渐扩展，原始裂纹扩展、新裂纹产生并不断发展，直至有规律的按一定方向逐渐汇合、贯通，形成大裂纹，最终导致试件破坏。对比图3中的各小图可以发现，裂缝生成位置基本相同，因此裂缝产生位置受砾石尺寸影响较小，而主要与微裂纹延伸方向和砾石分布特征有关。

图3 不同砾石尺寸模型最终破坏图Fig.3 The ultimate failure diagram of different gravel size models

图4 为不同砾石尺寸岩石模型的力学参数变化规律分布。由图4可知，随砾石尺寸的增加，岩心模型的泊松比与杨氏模量逐渐增加，当岩心中分布砾石后，杨氏模量会突然增大，而后随砾石尺寸的增大缓慢增加；随砾石尺寸的增加，单轴抗压强度变化规律比较复杂，砾石尺寸增大则基质的接触面积增大，基质发生破坏的面积增大，受岩心尺寸限制，当砾石半径大于1.6 mm后，由于砾石的分压作用，岩石强度则开始增加，因此抗压强度呈现先减小后增大的趋势。若砾石尺寸大于岩心尺寸则抗压强度达到最大，可以发现模拟规律与极限状态相一致，与实际情况相符。

图4 不同砾石尺寸模型力学参数曲线Fig.4 Mechanical parameter curves for different gravel size models

2.2 砾石强度的影响

测试新疆玛湖凹陷百口泉组地层砾岩岩心中砾石硬度，发现其差别很大，即存在强度很低的泥岩，也存在强度很高的灰岩。建立砾石尺寸、含量及分布特征均相同的岩心数值模型，仅改变砾石强度，分别赋值砾石强度为基质强度的0.2、0.4、0.8、2.0等倍数，研究砾石的强度对砾岩力学参数影响的规律。

图5为部分模型应力-应变曲线及破坏形式。从图5中可以发现，当砾石强度仅为岩石基质强度的0.2倍时，砾石首先破坏，破坏外模式为拉伸或剪切破坏。对比应力-应变曲线可以发现，当砾石强度较低时，岩石表现为塑性。随着砾石强度的增加，逐渐向脆性转变，岩石破坏方式由砾石最先开始破坏，随后砾石破坏数量和破坏程度逐渐减小，当砾石强度增大到基质的2.0倍以后，裂缝绕过砾石延伸且砾石完全不会破坏。

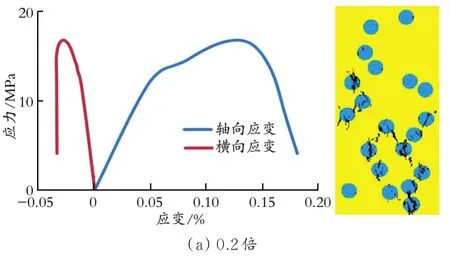
图5 不同砾石强度应力-应变曲线及破坏形式Fig.5 Stress-strain curves and failure modes of different gravel strengths

图6 为单轴抗压强度变化曲线。从图6中可以发现，随砾石强度的增大，岩石单轴抗压强度逐渐增大，当砾石强度增大到基质的2.0倍以后，岩石抗压强度保持不变，主要由基质强度决定。

图6 单轴抗压强度变化Fig.6 Uniaxial compressive strength variation rule

3 结 论

（1）相同强度的砂砾岩岩心在载荷加载过程中，首先在砾石边缘产生裂纹，不同砾石尺寸的岩心均表现为剪切破坏；岩心裂缝产生位置受砾石尺寸影响较小，而主要与微裂纹延伸方向和砾石分布特征有关；砾石尺寸越大，岩石破坏越严重。

（2）随砾石尺寸的增加，岩心模型的泊松比与杨氏模量逐渐增加；当岩心中分布砾石后，杨氏模量会突然增大，而后随砾石尺寸的增大缓慢增加；单轴抗压强度则随砾石尺寸增加呈现先减小后增大的趋势。

（3）砾石强度对砂砾岩破坏影响的研究发现，当砾石强度较小时，砾石会先于基质产生裂纹；而当砾石强度为基质的2.0倍时，裂缝绕过砾石延伸且砾石完全不会破坏。

（4）随砾石强度的增大，岩石单轴抗压强度逐渐增大，但砾石强度增大到一定值时，岩石抗压强度基本保持不变，主要由基质强度决定。