一种新型的基于KCS算法在图像重构中的应用
刘 艳,钱 阳,李 雷
(南京工业大学浦江学院,江苏 南京 211134)
1 概 述
1.1 压缩感知理论基础
在压缩感知理论[1-3]中,如果一组长度为n的被测信号x∈Rn×1在某正交基Ψ=(ψ1,ψ2,…,ψn)T上是可压缩的,则可以通过与稀疏变换基不相关的m×n维(m≪n)测量矩阵Φ对稀疏变换向量Θ=ΨTx进行观测,并通过一系列算法将原始信号x[4]从观测向量y∈Rm×1中重构出来,具体观测模型如下:
y=Φx=ΦΨΘ
(1)
压缩感知(CS)主要包括稀疏、观测和重构三个步骤[5],其中信号的稀疏性是CS的前提,在字典表示下信号的稀疏度决定了重构的效果。而测量矩阵Φ的设计则是压缩感知理论中至关重要的一步,Candès和Tao提出,为了准确地将原始信号重构出来,测量矩阵Φ需满足RIP(restricted isometry property)条件[6]。信号重构的数学模型如下:
(2)
其中,λ为正则化参数。
1.2 核压缩感知理论
Qi Hanchao等[7]将核技巧与CS理论结合,提出了核压缩感知理论(kernel compressed sensing,KCS),并将该理论运用到人脸图像的重构中,获得了较好的效果。KCS[8-9]本质上是一种非线性稀疏表示下的压缩感知,不仅能避开迭代的非线性优化过程,且与线性稀疏表示相比,能用更少的观测数目恢复信号[10]。
KCS理论中,若在特征空间H中,信号x是d稀疏的,则可以用一组稀疏基的d个原子将投影后的信号线性表示出来,即
(3)
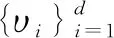
k(x,Φi)=〈φ(x),φ(Φi)〉=
(4)
在特征空间H中,所有测量值可以表示成如式5的矩阵形式,有:
(5)
将式5简写为:
Μkernel=Gkernelβ+ε
(6)

假设存在一组信号{z1,z2,…,zr}与原始信号x比较接近,通过KPCA方法对{z1,z2,…,zr}进行训练,则基原子υk可以表示成:
(7)
进一步,有:
(8)
结合式5,从而得到Gkernel的表达式为:
Gkernel=
(9)
(10)
由于任意信号都可以由一组正交基表示,且表示系数是其与稀疏基的内积。因此原始信号x∈Rn可以依据式11进行重构:
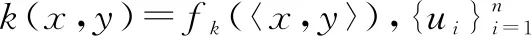
1.3 字典学习方法
1.3.1 K-SVD字典学习算法
基于过完备字典的稀疏表示是近年来广受关注的信号表示理论。其中,由Aharon M等提出的K-SVD字典学习算法[13]较为典型。此算法主要解决如下的优化问题:
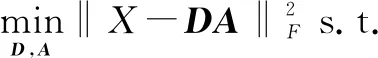
(12)
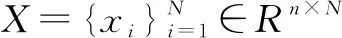
1.3.2 核字典学习方法(Kernel K-SVD,KKSVD)
KKSVD[14]算法的提出是用于实现核字典D的学习,该算法将目标由寻找合适的核字典D转化为寻找合适的字典系数矩阵C。
命题[15]:
存在一个合适的字典矩阵D*,使得
D*=φ(X)C
(13)
其中,C∈RN×K为字典系数矩阵。
此时,KKSVD算法求解的优化目标函数变为:
∀i=1,2,…,N
(14)
KKSVD算法通过获得最优的C和A对式14进行求解。
2 基于自适应核K-SVD字典学习的核压缩感知算法
(1)稀疏编码阶段。
文中将在KKSVD算法的基础上对该阶段进行改进。首先固定字典系数矩阵C,在特征空间引用AK-BRP算法[16]的稀疏编码机制,利用字典的相干性将稀疏约束上限与迭代更新的字典关联,获得自适应的稀疏约束上限,以减少算法运行时间。
设第j次迭代的稀疏约束上限为Tj,则
(15)
(16)
当μ(D)值很大时,则字典的相干性很大,即字典原子间相似程度很强[18]。
根据命题,核字典D可表示为D=φ(X)C的形式,此时有:
(17)
其中,K(X,X)=φ(X)Tφ(X)为核矩阵。
使用上述定义的ai代替KKSVD算法中的稀疏约束上界T0,由于式14中惩罚项可以写为:
(18)
因此,优化问题可以转化为求解如式19所示的N个问题。
T0,∀i=1,2,…,N
(19)
则所提AKKSVD算法的稀疏编码阶段可转化为求解如下的优化问题:
Tj,∀i=1,2,…,N,j=1,2,…,P
(20)
(2)字典更新阶段。
此阶段中,自适应核K-SVD算法采用KKSVD算法的字典更新方式,根据稀疏表示系数矩阵A,对字典系数矩阵C进行迭代更新,字典列的更新结合稀疏表示的一个更新,使得字典系数和稀疏系数同步更新。
综上,AKKSVD字典学习算法的具体实现流程如下:
算法1:AKKSVD算法。
目标:获得字典系数矩阵C
输出:矩阵C和A
初始化:随机初始化归一化字典系数矩阵C0∈RN×K,通过式15获得T0,设置迭代次数j=1
Forj=1,2,…,P
(1)稀疏编码阶段
固定Cj-1和Tj-1,使用KOMP[14]算法求解式20,获得稀疏系数矩阵Aj
(2)字典更新阶段
固定Aj,对Cj-1的每一列ck(k=1,2,…,K)逐个更新
获取更新后的Cj
通过式15计算Tj;j=j+1;
End

(21)
其中,εt为误差,〈·〉表示内积。
通过AKKSVD算法获得核字典系数C,则图像块在特征空间Η中的稀疏表示如下:
φ(xt)=Dat=φ(X)Cat
(22)
其中,C∈RN×K,at∈RK×1表示第t块图像的稀疏表示系数
根据KCS理论,所有测量值在特征空间Η中表示成:
(23)
定义
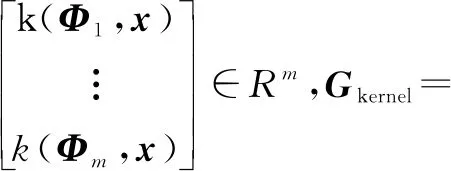
(24)
根据
ykernel=GkernelCa
(25)
令Bkernel=GkernelC,则
ykernel=Bkernela
(26)
其中,ykernel∈Rm,Bkernel∈Rm×K。
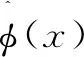
(27)
并将恢复出的原始空间的图像块按照顺序合并成整个图像。
AKKSVD-KCS算法的具体流程如下:
算法2:AKKSVD-KCS算法。
初始化:通过KPCA方法从X中获得特征空间中的基原子,利用其初始化AKKSVD算法中的字典原子,并通过式15获得初始化稀疏约束上限T0,设置迭代次数j=1
利用AKKSVD算法从X中获得核字典系数C=CP
通过式24计算出ykernel及Gkernel
获得式26的欠定方程组
3 仿真实验及结果分析
为了更直观地比较AKKSVD-KCS算法与KKSVD-KCS算法重构出图像的视觉效果,图1给出了采样率为0.4时这两种算法重构出标准图像的视觉效果图。

图1 标准图像的视觉效果
图1中显示,当采样率为0.4时,KKSVD-KCS算法和AKKSVD-KCS算法均能将图像重构出来。两种算法重构出的图像虽然都有分块边界,但可以看出,相较于KKSVD-KCS算法,AKKSVD-KCS算法的分块边界相对模糊,这表明提出的AKKSVD-KCS算法的重构性能更优。
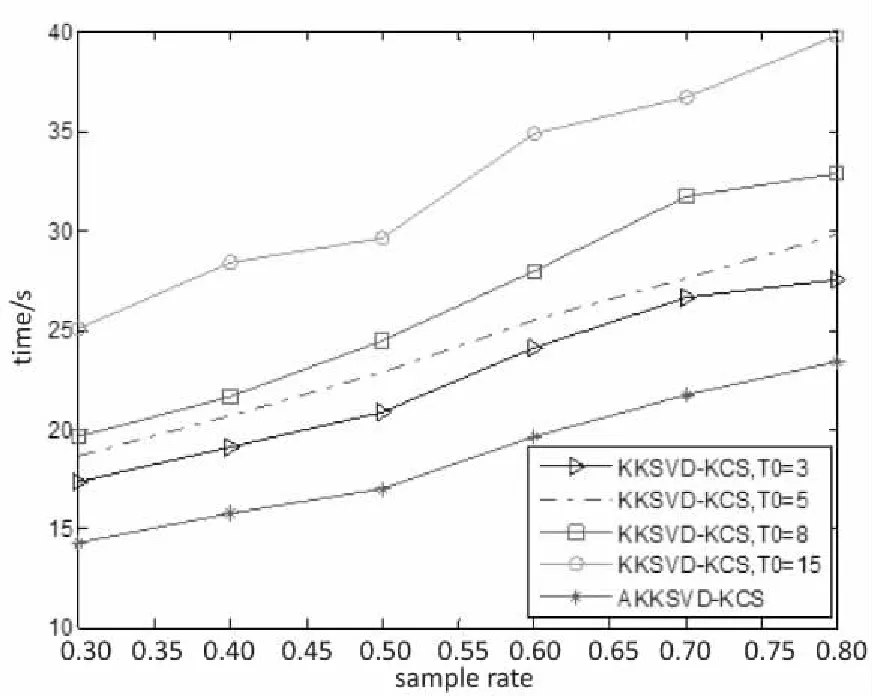
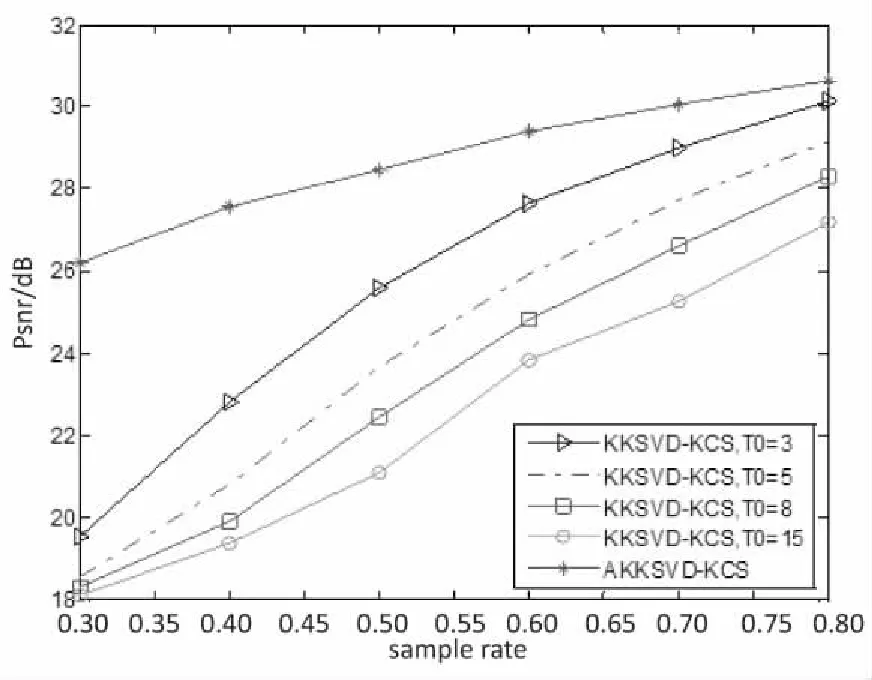
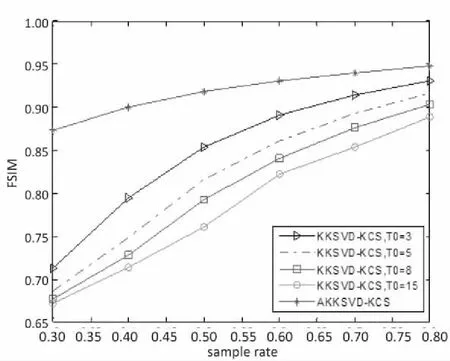
为了进一步验证提出算法的优越性,图2分别给出了KKSVD-KCS算法在不同稀疏度下与AKKSVD-KCS算法在重构时间、峰值信噪比以及特征相似度三个方面的性能与采样率的关系曲线。为了消除随机性,PSNR与FSIM值取10次测试结果的平均值。
由图2(a)可知,各算法的运行时间均随着稀疏度的增加而增加,但AKKSVD-KCS算法的运行时间是最少的;图2(b)、2(c)的结果表明,AKKSVD-KCS算法的PSNR与FSIM均随着稀疏度的增加而增加,由PSNR和FSIM越大,重构性能越好可知,相较于KKSVD-KCS算法,AKKSVD-KCS算法的性能更优,精确度更高。
综上可知,AKKSVD-KCS算法在每次迭代过程中通过自适应地选择较小的稀疏度以提高运行速度及重构精度,进一步验证了非线性流行下该算法的有效性和高效性。
(a)
(b)
(c)
4 结束语
文中在核K-SVD字典学习算法的基础上提出了AKKSVD算法,通过选择较小的稀疏度以提高运行速度,并结合核压缩感知的相关理论,提出了AKKSVD-KCS算法,实现了对原始空间图像的重构。仿真对比实验表明,AKKSVD-KCS算法的重构性能更优。

