基于迭代加权低秩分解的遮挡人脸识别算法

虞 涛，童 莹，曹雪虹

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京工程学院 通信工程学院，江苏 南京 211167)

0 引 言

近年来，基于稀疏表示的方法在人脸识别中得到了广泛应用。针对非约束环境下的人脸识别研究逐渐成为了当今世界人脸识别领域中的热点问题，如何处理光照、遮挡、年龄等干扰因素，已成为计算机视觉领域所面临的一个核心问题。Wright等率先把稀疏表示的理论思想和分类问题结合起来，提出了稀疏表示分类(sparse representation based classification，SRC)方法[1]，从稀疏的角度将待测样本图像表示为训练样本图像的线性组合。Nguyen等[2]通过训练样本构建多尺度字典，分别对待测样本进行稀疏表示，利用权重投票机制进行分类识别。Yang等[3]针对稀疏表示中范数最小化的求解问题提出了新的优化算法，减少了光照、遮挡和表情等干扰因素的影响。付宁等[4]针对实际应用中信号块稀疏度未知的情况，提出了一种块稀疏度自适应迭代算法用于信号重构。Yang Meng等[5]提出鲁棒稀疏编码方法来寻求稀疏编码问题上最大似然估计解，在处理人脸遮挡，光照和表情变化方面有效果。Deng Weihong等[6]提出辅助类内变化字典来表示训练和测试图像之间的变化。胡正平等[7]针对阴影、遮挡等原因破坏图像低秩结构这一问题，提出基于低秩子空间恢复的联合稀疏表示识别算法。

传统子空间理论通常认为单一个体的人脸图像位于同一个低秩子空间中，然而由于光照、遮挡、姿态、表情、年龄等干扰因素，实际获取的人脸图像很少能够显示低秩结构，影响分类性能。Candes等[8]提出低秩矩阵分解(robust principal component analysis，RPCA)即鲁棒主成分分析，将受到噪声干扰的训练样本分解为低秩矩阵和稀疏误差矩阵，通过低秩矩阵构建字典进行分类判别。Chia-Po Wei等[9]针对训练和测试图像数据由于遮挡或伪装而被破坏的情况，提出了基于低秩矩阵分解的新型人脸识别算法，引入结构不连贯约束，对训练样本进行低秩分解，分解为类间差异大的基底。He Ran等[10-11]通过用非凸M估计量取代误差项的1范数，可以精确恢复严重受损的低秩矩阵。

人脸识别过程中，对测试样本进行分类判别得到较差的识别率，原因在于受遮挡干扰会改变人脸图像原本的特征和增加错误的图像，从而对识别结果造成不利的影响，为克服遮挡等因素，构建更加有效的字典也是至关重要的。通过迭代加权低秩分解算法得到的遮挡字典可以充分地表示训练和测试样本中的噪声因素。文中提出的方法对于遮挡干扰因素具有很好的鲁棒性。

1 相关算法

1.1 稀疏表示分类算法

稀疏表示的基本原理是在利用有限个信号通过线性组合表示一个自然信号时，只有为数不多的几个信号对应的表示系数值非零，而其他信号对应的系数值都为0。对未知类别的待测试人脸图像，利用已知的训练样本集对它进行线性表示，通过计算待测样本的重构表示系数值，再利用各类样本及其对应的表示系数做重构残差比较，选择最小残差值的样本类别作为待测试图像的所属类别。

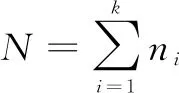
(1)

其中，y为待测试样本；D为由训练样本集构成的字典；α为待求解的稀疏表示系数。

目标函数中利用1范数近似代替0范数来约束表示系数的稀疏性[3]。对于上述最小化问题，文中采用梯度投影重构法[12](gradient projection for sparse reconstruction，GPSR)分析计算。在计算得到稀疏表示系数后，SRC根据系数向量在每类样本上进行重构表示，通过计算待测试样本和各类重构样本之间的残差，比较并选择最小残差的样本类别作为待测试人脸图像的所属类别。目前，稀疏表示分类方法已经在很多领域得到了广泛的应用[13-15]。

1.2 低秩矩阵分解算法

在理想的子空间假设情况下，D应该是低秩的，由于干扰，D呈现满秩的特征，可以将问题抽象描述为：已知训练样本矩阵D，可以将D表示为D=A+E，且低秩矩阵A和稀疏矩阵E是未知的，但由训练样本D的构成可知A具有低秩的特征，E是稀疏的且矩阵中非零的元素可以任意大、数目尽可能少。基于上述问题，可提出以下的等价结论：寻求测试字典矩阵D中主成分矩阵A的最小秩矩阵且具有低秩特征，且误差矩阵E是稀疏的，即非零元素数目尽可能少。于是形成了如下优化问题：

(2)

其中，rank(·)表示一个矩阵的秩；‖·‖0表示一个矩阵中非零元的个数。

通过对式2做松弛优化可以把问题转化为一个易于解决的凸优化问题，即用1范数代替0范数，用核范数代替秩函数，式2就转化为式3所示的易于求解的凸优化问题。

(3)

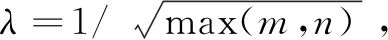
2 基于迭代加权低秩分解算法

正如之前在引言中提到的扩展稀疏表示算法，构建辅助类内变化字典来表示训练和测试图像之间由干扰所引起的差异。但扩展稀疏表示算法构建的扩展字典对于遮挡干扰因素具有较差的识别结果。对于字典来说，应该充分描述训练样本和测试样本中的遮挡因素，而且同一类人脸的字典中不应该包含类间信息，如果同一类人脸的字典包含了其他类的人脸信息，那么在稀疏重构时就会出现错误。

为了解决遮挡干扰因素的影响，该小节提出基于迭代加权低秩矩阵分解算法构建自适应遮挡字典的方法。因为通过低秩矩阵分解算法恢复的低秩矩阵已足够正确，而文中提出的方法是关于训练样本和测试样本中被遮挡因素影响的部分，并且该部分不包含类间信息。对于训练样本，该算法能得到被遮挡因素影响的信息。对于测试样本，在分类之前测试样本所属类别未知，测试样本与不同类的人脸矩阵通过低秩矩阵分解得到的矩阵中包含类间信息，因此文中提出的算法能得到该测试样本中包含遮挡所掩盖的信息，同时除去其他未被遮挡部分的类间信息，并将得到的信息作为每一类人脸的扩展字典。因此，迭代加权低秩矩阵分解算法可以描述为以下优化问题：

(4)

其中，W⊗E表示W是一个权值矩阵，当Eij包含噪声时，Wij被赋予一个近似于1的值，即(W⊗E)ij=Wij·Eij。事实上，遮挡的分布情况是未知的，权值矩阵只能通过一个迭代加权策略来一步一步近似它，因此，选取逻辑函数w(x)=1/(1+exp(μη-μx2))作为加权函数。其中μ和η是正标量，参数μ控制下降速率，参数η控制分界点的位置。经过大量实验得出图片像素值归一化到0和1之间时，μ和η的值取9和0.1可获得最佳效果。

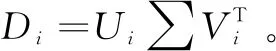
(5)

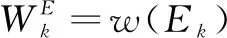
基于非精确拉格朗日乘子法的加权低秩矩阵分解算法：

输入：数据Di∈Rm×ni，正则化参数λ，权值参数σ和ξ；

初始化：Y0,A0=0,E0=0,W0=w(E0),k=1；

输出：W⊗E。

迭代步骤：

1)更新Ek：

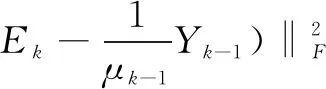
(6)

2)更新Wk：Wk=f(Ek)

3)更新Ak：

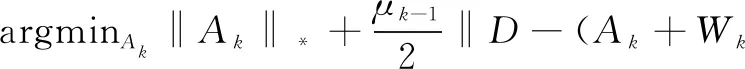
(7)

4)更新Yk,μk：

Yk=Yk-1+μk-1(D-Ak-Wk⊗Ek)，

μk=min(ρμk-1,μmax)，ρ>1

(8)

5)检测停止条件，如果不满足，k=k+1，重复上述步骤1-5，否则，停止迭代，输出W⊗E

根据文献[17]，通过奇异值收缩阈值算子(singular value thresholding，SVT)，能够得到如下的闭式解：

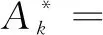
(9)

将Fk=Wk-1⊗Ek带入式6，根据文献[18]通过奇异值收缩算子，能够得到如下的闭式解：

(10)

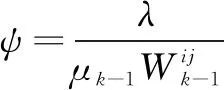
基于迭代加权低秩分解算法的人脸识别算法对某一测试y∈Rm×1的分类步骤如下：

输入：测试样本y∈Rm×1，训练样本Di∈Rm×ni

1)FOR i=1:k

2)利用加权低秩矩阵分解训练的样本Di，得到Wi⊗Ei

3)利用低秩矩阵分解训练样本Di，得到Ai和Ei

4)利用加权低秩矩阵分解Xi=[Ai,y]，取结果矩阵的最后一列得到Wi(ni+1)⊗Ei(ni+1)

5)END FOR

6)构造字典Zi=[Ai,Wi⊗Ei,Ei-Wi⊗Ei,

Wi(ni+1)⊗Ei(ni+1)]，Z=[Z1,Z2,,Zk]

7)利用稀疏表示分类算法对y进行稀疏表示，根据式1进行分类识别

输出：测试样本y所对应类别

3 实验仿真

为了验证算法的有效性，将提出的基于自适应噪声字典的人脸识别算法和其他算法(LR-SRC[7]、ESRC[6]、SRC[1])进行比较。采用AR人脸库和Extended Yale B库进行实验。

3.1 AR库

AR人脸数据库包含126个人的4 000多幅正面对齐人脸图像，其中光照变化图像8张，表情变化6张，眼镜遮挡图像6张，围脖遮挡6张。该实验选取了100类样本，并进行裁剪及归一化处理，裁剪后的尺寸为50×40。图1为AR人脸库中某类人的一些样本图像。

图1 AR库的样本图像

实验包括两部分，实验1选取AR数据库中每类样本中第一部分的前7幅无遮挡图像和任意1张含有眼镜遮挡图像作为训练样本，第二部分的前7幅无遮挡图像和两部分中剩余的5张含有眼镜遮挡图像作为测试样本。实验2选取AR数据库中每类样本的第一部分前7幅无遮挡图像和任意1幅含有围脖遮挡图像作为训练样本，第二部分中前7幅无遮挡图像和两部分中剩余的5幅含有围脖遮挡图像作为测试样本。表1是AR库人脸图像在不同方法下的平均识别率。

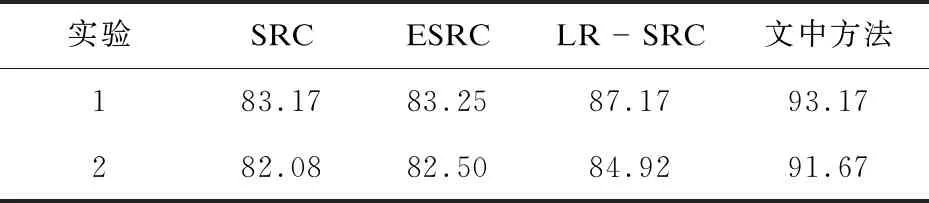
表1 AR库图像的实验结果 %

从表1可以看出，对AR人脸库原图像进行分类识别，在实验1中文中算法取得了93.17%的识别率，比LR-SRC、ESRC、SRC等算法识别结果分别提高6%、9.92%、10%。在实验2中文中算法取得了91.67%的识别率，比LR-SRC、ESRC、SRC等算法识别结果分别提高6.75%、9.17%、9.59%，识别效果有明显提高，主要原因在于利用迭代加权低秩矩阵算法可以得到遮挡所掩盖的信息，遮挡矩阵很好地描述了训练样本和测试样本中的遮挡因素。结果显示了对于眼镜和围巾等遮挡具有良好的鲁棒性，充分验证了文中算法的可行性和有效性。

3.2 Extended Yale B库

Extended Yale B库包含38类人在光照条件变化的情况下获得的人脸照片，图像大小为192×168，每类人有大约64张，共2 414张正面对齐图像。实验中选取有64张图像的人脸作为实验数据，共2 414张图像，并且每张图像大小裁剪调整为50×40大小，并进行归一化处理。图2为Extended Yale B人脸库中某类人的一些样本图像。

实验分别在每类中取出10幅图像作为训练样本，其余54张作为测试样本。表2是在Extended Yale B库人脸图像利用不同方法的识别率。

从表2可以看出，文中算法的识别率相比其他算法有很大提升，提高到92.54%，可以看出迭代加权低秩矩阵算法对于光照具有良好的鲁棒性。主要原因在于利用迭代加权低秩矩阵算法实现过程中同时考虑了训练样本和测试样本中光照所影响的信息，从而更好地提高了识别率。

表2 Extended Yale B库图像的实验结果

图2 Extended Yale B库的样本图像

4 结束语

文中提出了基于迭代加权低秩分解的遮挡人脸识别算法，通过该算法提取训练样本和测试样本中的遮挡信息，在遮挡信息中保留了遮挡的部分，移除了类间信息的干扰，提高了人脸图像的识别率。相比其他算法，该算法可以应用于各种形状的遮挡。通过人脸库测试结果表明，该算法识别结果较好，对干扰具有良好的鲁棒性，尤其是在训练样本和测试样本均含有遮挡的情况下有明显提高。