基于有限元法对异步电动机电磁噪声分析与优化
(中车株洲电机有限公司,湖南株洲 412001)
0 引言
电机中产生的三大类噪声包括电磁噪声、空气动力噪声和机械噪声,其中电磁振动噪声是由气隙磁场与定子结构耦合产生的。为了减小电机体积要增加电机的电磁负荷,导致磁饱和,力波含量增加,激振力波与振型产生共振时会产生更严重的电磁振动与噪声问题。
由于用等效电路法只能近似计及转子导条内的电流集肤效应和电机饱和现象,采用有限元法来计算电机内的电磁场可提高计算精度。电机包含多种形状复杂的部件,有限元法可更准确的计算电机的振动模态。准确的计算电机电磁场特性和振动模态是准确计算电磁噪声的前提条件。
1 电机电磁力波分析
气隙中一系列定转子磁场相互作用可以产生数量很多的电磁力波,从噪声和振动的观点看,主要有主波磁场产生的力波、定子绕组和转子绕组谐波磁场产生的力波,以及定子气隙磁导一阶齿谐波和转子气隙磁导一阶齿谐波磁场所产生的力波[1]。某款额定功率为800kW,极数6极的三相异步电动机参数为:额定电压600V,额定频率50Hz,定转子槽比72/62,绕组星形连接。根据文献[1]该电机定子齿所受径向力波阶次如表1(仅列至定转子一阶齿谐波)。

表1 定子齿受的主要径向力波阶次
各次力波的频率计算公式为
(1)
式中,μ0—空气磁导率;Bμ—转子谐波磁场;Bν—定子谐波磁场;μ—转子谐波次数;ν—定子谐波次数;θ—转子机械角位移;ωμ—转子谐波相对定子的角频率;ων—定子谐波相对定子的角频率;φμ—转子谐波初相角;φν—定子谐波初相角[1]。由于低阶力波产生的振动和噪声较大,计算主波磁场产生的r=6次力波频率为100Hz,定转子谐波产生的r=-2和r=-4次力波频率为1012Hz。
将电机参数输入某有限元软件,计算得空载电流231A(试验空载电流225A),电机定子受力见图1,定子上一点径向力傅里叶分解见图2。由图1知空载时电机定子主要为齿部受径向力,由图2知径向力中100Hz和1000Hz的分量较大,超过3000Hz以后的径向力非常小,与前述理论分析相符。
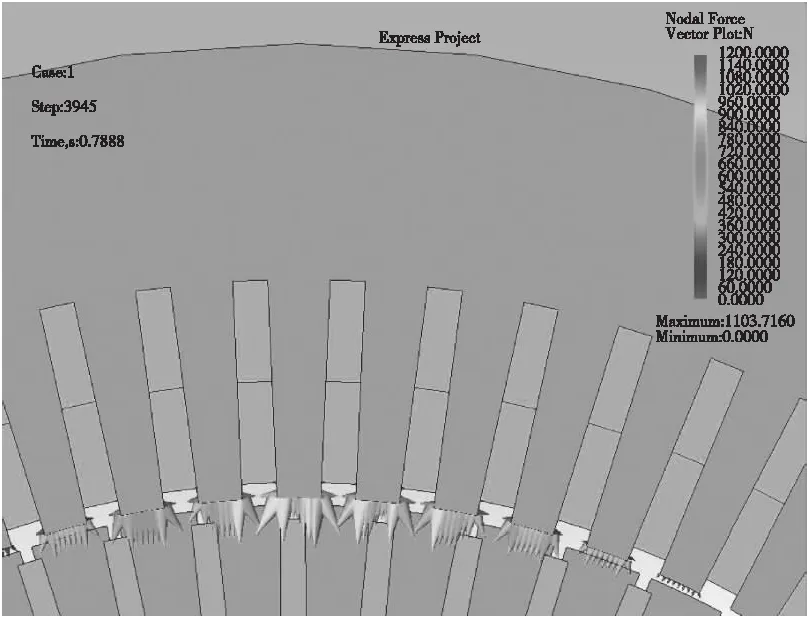
图1电机空载时定子受力分布图
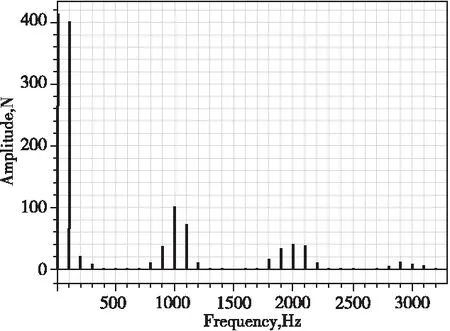
图2电机定子径向力波频率分布
电机定子某一时刻周向空间电磁力波形的傅里叶分解图见图3,由图3知主波磁场产生的r=6阶分量较大。利用一维傅里叶分解法只能对径向力随时间变化进行分解得到径向力频率的分布情况,或者对径向力随空间变化进行分解得到径向力阶次分布情况,这样得到的结果是力波时间分解中含有各次空间谐波分量,力波空间波形分解结果中含有各次时间谐波含量。力波对电机振动和噪声的影响与力波的幅值、阶次和频率同时相关:定子铁心的变形量约与力波阶次的四次方成反比[1];电机铁心和机座都有一定的固有频率。当电磁力波的空间波形和时间频率与铁心和机座振动的振型和频率相接近甚至相同时会产生共振,这时铁心振动及辐射的噪声将大大增大,将电磁力的空间和时间分量组成的矩阵做二维傅里叶分解结果如图4所示。
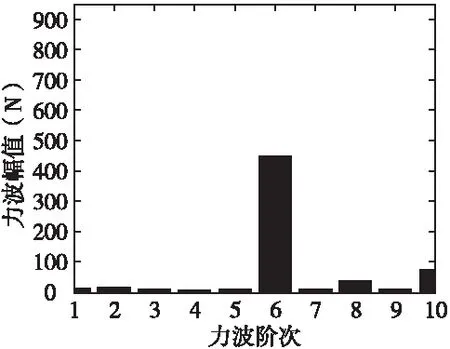
图3电机空载时定子受力分布图
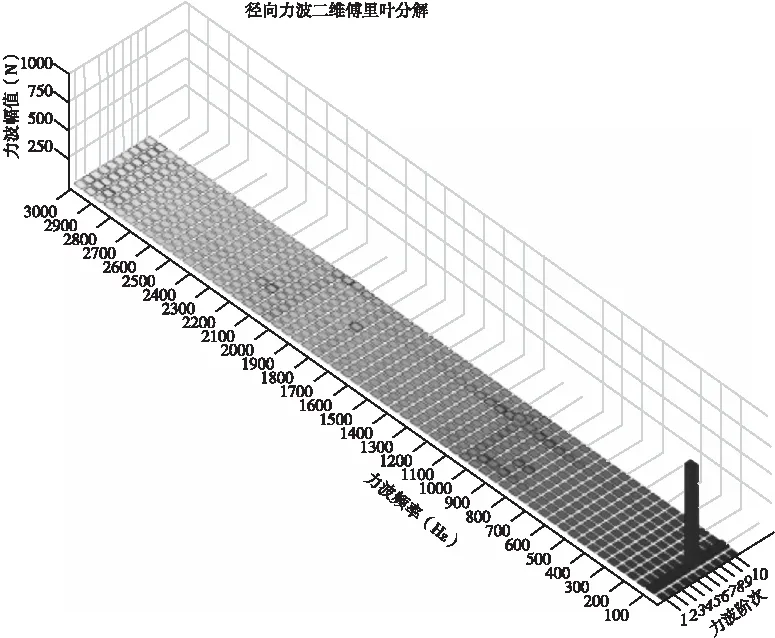
图4电机空载时定子径向力波二维傅里叶分解
由图4知电机径向力波中主要阶次谐波的频率和幅值见表2。
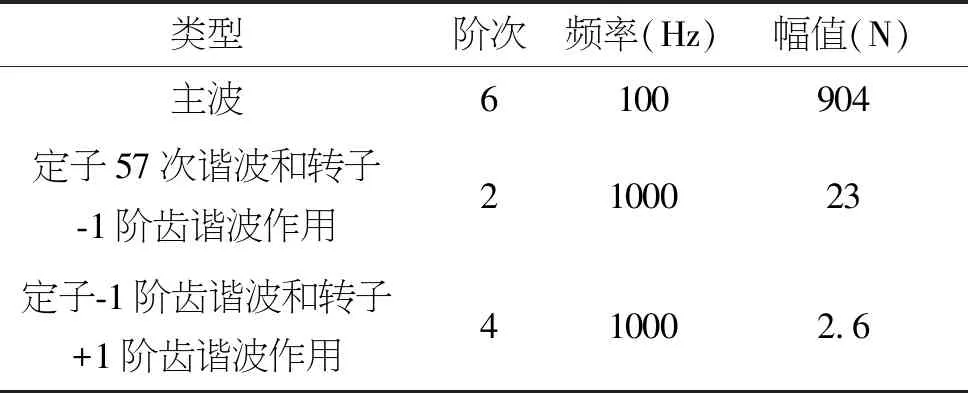
表2 电机径向力波中主要阶次谐波的频率和幅值
2 电机振动模态有限元分析
预测电机的振动和噪声需要准确计算电机定子结构的固有频率和定子的响应特性。振动模态分析,就是利用系统固有模态的正交性,以系统的各阶模态向量组成的模态矩阵作为变换矩阵,对选取的物理坐标线性变换,使得振动系统以物料坐标和物理参数所描述的、互相耦合的运动方程变为一组彼此独立的模态方程。
2.1 电机的转子结构的重力对于定子结构属于静态载荷,会影响它的刚度矩阵,进而影响其固有频率[2],为提高计算速度,本文把转子建为质量点。电机风机建为质量点施加机座上,不考虑接线盒影响。
2.2 叠片结构铁心弹性模量的确定
针对本电机建立三维模型,由于电机铁心结构主要由正交各向异性硅钢片叠压而成,因此定子不能当做一个材料均匀的连续弹性体[3]。把垂直于叠片平面的方向定义为1(电机旋转轴方向),叠片所在平面定义为2~3平面,叠片平面认为各向同性,E2=E3,而垂直于叠片平面的方向上E1低于硅钢。剪切模量G23和G13相等,G12不同。G12依据正交各向异性材料确定,G23和G13取硅钢的90%。定子铁芯材料属性见表3。
2.3 绕组参数的分析与影响
本电机绕组是由若干铜扁线在外包绝缘带后定型成的整体,铜线各向同性,线性弹,但绕组整体正交各向异性。建模时假设定子齿和绕组紧密接触,但绕组的刚度远低于实体铜,绕组贡献的刚度取决于槽满率,相邻绕组之间的间隙决定E值。绕组在纤维方向的弹性模量E1小于实体铜,但大于E2和E3。G12按复合材料弹性参数的计算方法确定[4]。各方向的泊松比均取0.3,绕组的属性见表3。
中大型异步电机绕组对定子固有频率有很大的影响,不考虑绕组时,定子固有频率误差达30%,计算固有频率时不能忽略绕组的影响。端部贡献质量与贡献刚度大体抵消,因此本电机计算时仅考虑绕组有效部分而不考虑绕组端部[3]。

表3 定子材料属性
2.4 振动模态分析结果
电机地脚施加固定约束,定子2阶振型的振动频率为1072Hz,定子形变主要为径向,可与定子径向力发生共振,振动模态见图5。
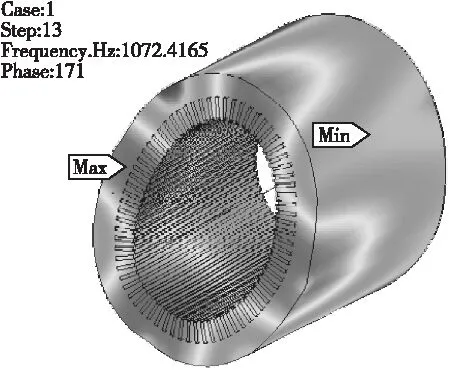
图5定子径向振动的椭圆模态
3 电磁噪声的计算及优化
将第1部分的计算的电磁力节点数据导入到第2部分计算的结构场中,经过网格之间的插值映射,进行电磁场和结构场的耦合计算,求解得出电磁振动和噪声的频响结果。由于定子2阶振型的固有频率为1072Hz,与2阶力波的1000Hz分量较为接近,二者将会产生共振,计算得最大噪声的频率为1125Hz。同时,由于2阶基波的100Hz分量的幅值较大,电机100Hz的电磁噪声较大。电机周围1m的噪声云图见图6,计算噪声频谱与试验值对比见图7,由图可知较大的电磁噪声分布在机座径向周围,计算的频谱总体趋势与试验值基本符合。计算噪声最大值小于试验值,这主要是由计算值未考虑背景噪声及模态计算时材料属性误差引起。
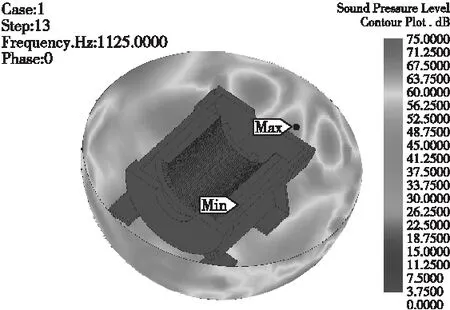
图6电机周围1m内1125Hz噪声云图

图7计算噪声频谱与试验值对比
根据前述分析,为了降低电机电磁噪声,可通过调整电磁方案消除2阶力波的幅值或改变电机2阶振型的频率,或加强机座刚度减定子变形量。本文计算了将原来电机定子铁心与机座间的支撑筋由10根45厚筋改为16根20厚的筋,以改变铁心弯曲时力波相邻节点间的变形量的改进方法,这样重新计算后电磁噪声最大值降低约5dB,优化前后的电磁噪声计算对比见图8。
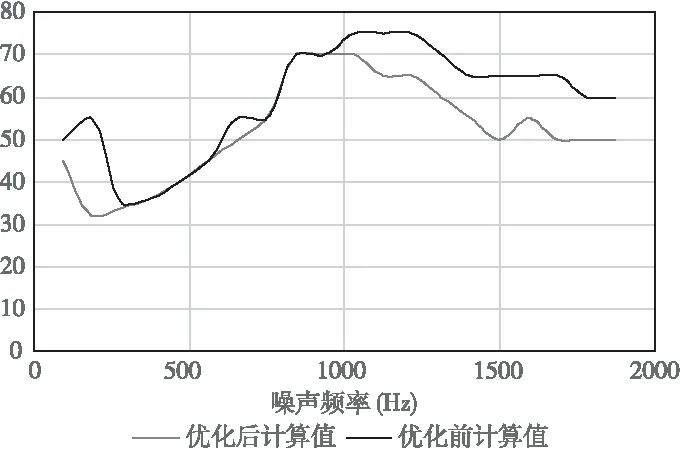
图8优化前后的电磁噪声计算对比
4 结语
通过有限元分析及与试验值比较,确认了计算方法可近似计算三相异步电动机电磁噪声的频谱分布,并对结构优化方案进行了电磁噪声预测,得出该方案不仅减轻了电机重量而且可降低电机噪声最大值约5dB。由于原电机噪声测量的误差、计算模态时材料属性未考虑浸漆的影响、模型的简化方法等因素,优化方案的实际效果需待电机生产后试验最终确认。

