高速铁路信道小尺度衰落与非平稳特性研究

周 涛，李华玉，秦鑫彤，文 辉，陶 成

(1.北京交通大学 电子信息工程学院，北京 100044；2.东南大学 移动通信国家重点实验室，江苏 南京 211189)

《中长期铁路网规划》勾画了新时期“八纵八横”高速铁路网的宏伟蓝图，预示着我国高速铁路发展更进一步。随着高速铁路的快速发展，无线通信系统面临的挑战越来越大，如何保证在高速移动条件下为用户提供更高的带宽、更低的时延、更可靠的通信质量[1]，将是面临的主要问题，掌握高速铁路环境下的无线信道特性对于高铁通信系统的设计具有重要意义。

信道特性的研究必须要有大量的实测数据作为支撑。在高速铁路环境下，由于列车运行里程长，周围环境复杂多变，并且信道测量活动需要铁路部门的配合，因此对信道特性研究带来了一定的困难[2]。近些年来，相关研究人员克服困难，进行了大量的高速铁路信道测量活动，并对测量结果进行分析，取得了丰硕的成果。文献[3]在哈尔滨—大连的高速铁路沿线进行了信道测量活动，分析平原场景下的大、小尺度衰落特性。文献[4]利用Propsound信道探测仪进行信道测量，分析高架桥场景下的大尺度和小尺度衰落特性。文献[5-6]针对高架桥场景，提出一种基于距离的莱斯K因子模型。文献[7]利用GSM-R(Global System for Mobile Communications - Railway)信号在郑州—西安高速铁路沿线进行了测量活动，主要研究了阴影衰落的自相关特性，并提出一种自相关模型。文献[8]基于实测数据，重点研究了U形槽场景下的小尺度衰落特性。文献[9]在京沪高速铁路沿线进行了测量活动，并建立一种基于几何的随机簇模型。文献[10]基于武汉—广州高速铁路沿线的信道测量数据，分析了大、小尺度统计特性。文献[11]研究了地表起伏较大的丘陵环境下的大尺度衰落特性和莱斯K因子。文献[12]基于车站环境下的实测数据，提出一种扩展的Hata模型。

从现有文献来看，还存在一些不足之处。大部分文献都是针对单一高速铁路环境下的信道特性进行研究，并且主要关注大、小尺度衰落的一些常见参数，研究角度特性与非平稳特性的较少。

为了进一步弥补高铁信道特性研究的不足，本文采用LTE(Long Term Evolution)信道探测仪对京津城际高铁线进行无线信道测量，获得了真实场景下的测试数据，以此为基础，对比分析了平原、车站、城郊3个典型的高速铁路场景下的信道小尺度衰落特性，如莱斯K因子、均方根RMS(Root Mean Square)时延扩展、到达角、功率角度谱等特征参数。此外，从两个角度研究了高速铁路信道的非平稳特性：以功率相关性为基础，分析了高速铁路信道的稳态间隔；采用马尔科夫链模型，描述了高速铁路信道多径的动态变化。

1 测量描述

在高速铁路测量活动中，采用自主研发的LTE信道探测仪。探测仪由两个射频模块、一个同步模块、一个数据采集模块、一个数据存储介质和一个高性能计算机等部分组成，其原理图如图1所示。

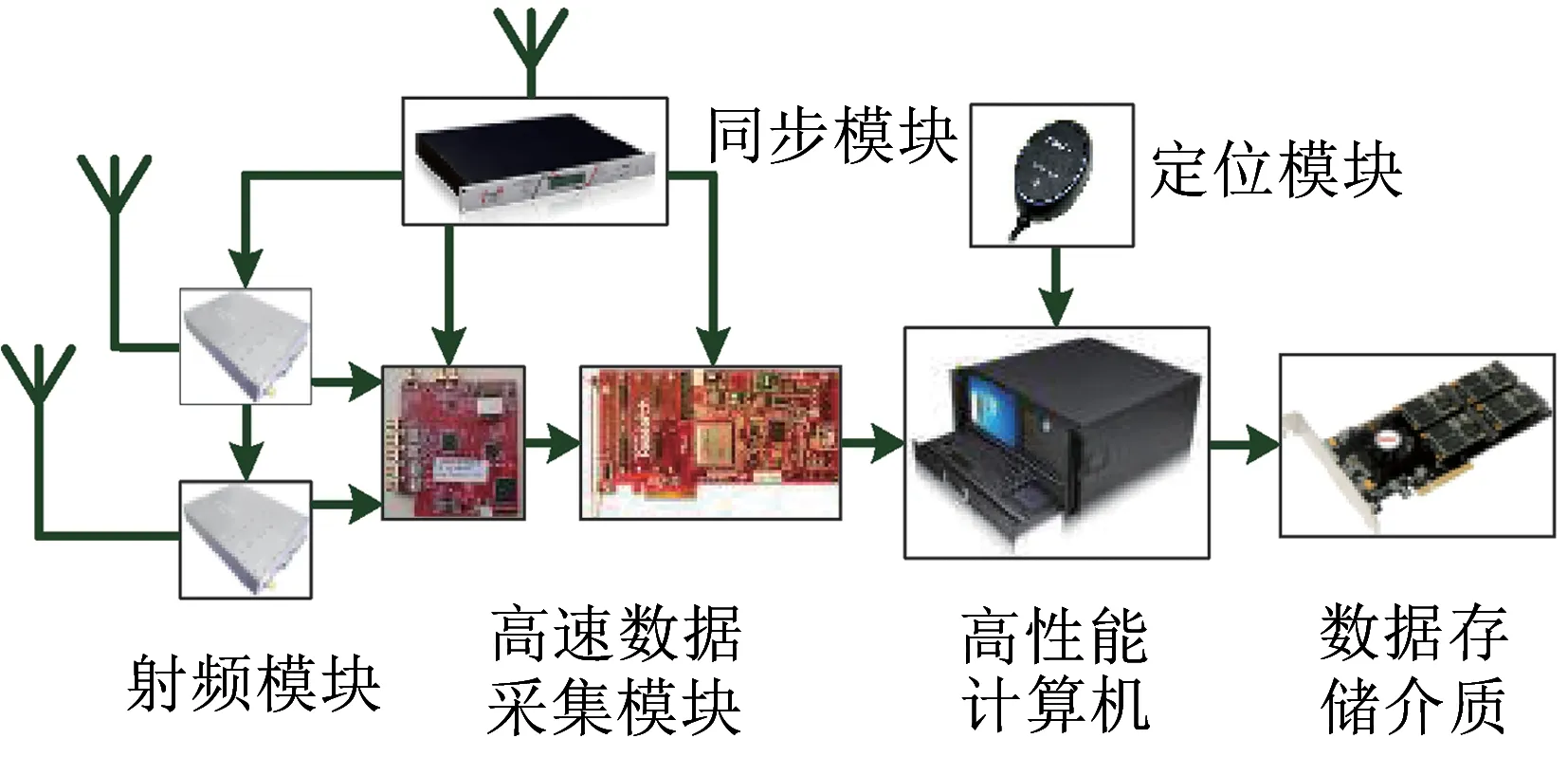
图1 LTE信道探测仪原理图

该信道探测仪在使用时并不发射探测信号，因为它没有发射机，只有接收机，这也是与传统信道探测仪的不同之处。该信道探测仪利用LTE信号中的小区参考信号CRS(Cell Reference Signal)作为信道的探测信号，当接收到LTE信号以后，通过与本地CRS的自相关，获得信道冲激响应，进而提取其他信道特征参数。

本次测量在LTE铁路专网上进行，铁路沿线的LTE基站上部署了信号发射端，LTE信道探测仪位于高铁车厢顶部，在高速铁路列车运行过程中，接收天线作为接收端，连续采集LTE网络下行链路的数据。详细的测量参数见表1。

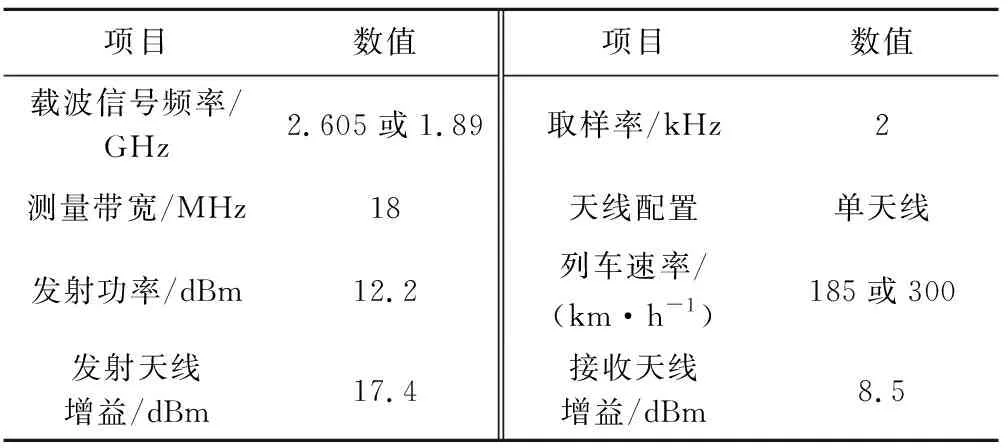
表1 测量系统参数

本次测量线路选择京津城际高速铁路沿线的两段。第一段以平原场景为主，如图2所示，范围是天津站到亦庄站，在该段路程中列车运行速度为300 km/h，接收信号的载波频率为1.89 GHz。途中经过天津武清站时，车站前后范围约440 m的距离内，分为约14 m宽的两边，在这两边之中有宽为9 m的无遮挡部分，如图3所示。区域在本文中作为平原场景和车站场景进行研究。第二部分主要是城郊场景，由亦庄站到北京南站，是从郊区到城市的线路，如图4所示。在该段中列车运行速度为185 km/h，接收信号的载波频率为2.605 GHz。该段区域建筑物主要是低矮的民居，但建筑物密度与城市环境相似，所以此区域既区别于城市环境，又区别于偏远郊区，在本文中作为城郊场景进行研究。城郊场景的边缘处存在较高的居民楼，所以结果可能会有一定的偏差。另外，由于高速铁路信道测量活动的复杂性，本次测量活动只进行了一次，因此论文中所有的统计结果都是一次测量的结果，不具有一般性。

图2 平原场景

图3 车站场景

图4 城郊场景

2 小尺度衰落特性分析

2.1 莱斯K因子

在无线传播环境中，接收机收到的信号包括直射分量与多径分量，一般用莱斯K因子来描述接收信号中直射径与非直射径的能量强度之比。莱斯K因子反映了衰落的严重程度，K值越小，表示衰落越严重。在实际的数据处理中，常见的K因子估计方法为矩估计法[13]。通过该方法，本文得到3个场景下K因子的累积分布函数CDF (Cumulative Distribution Function)拟合结果对比，如图5所示。

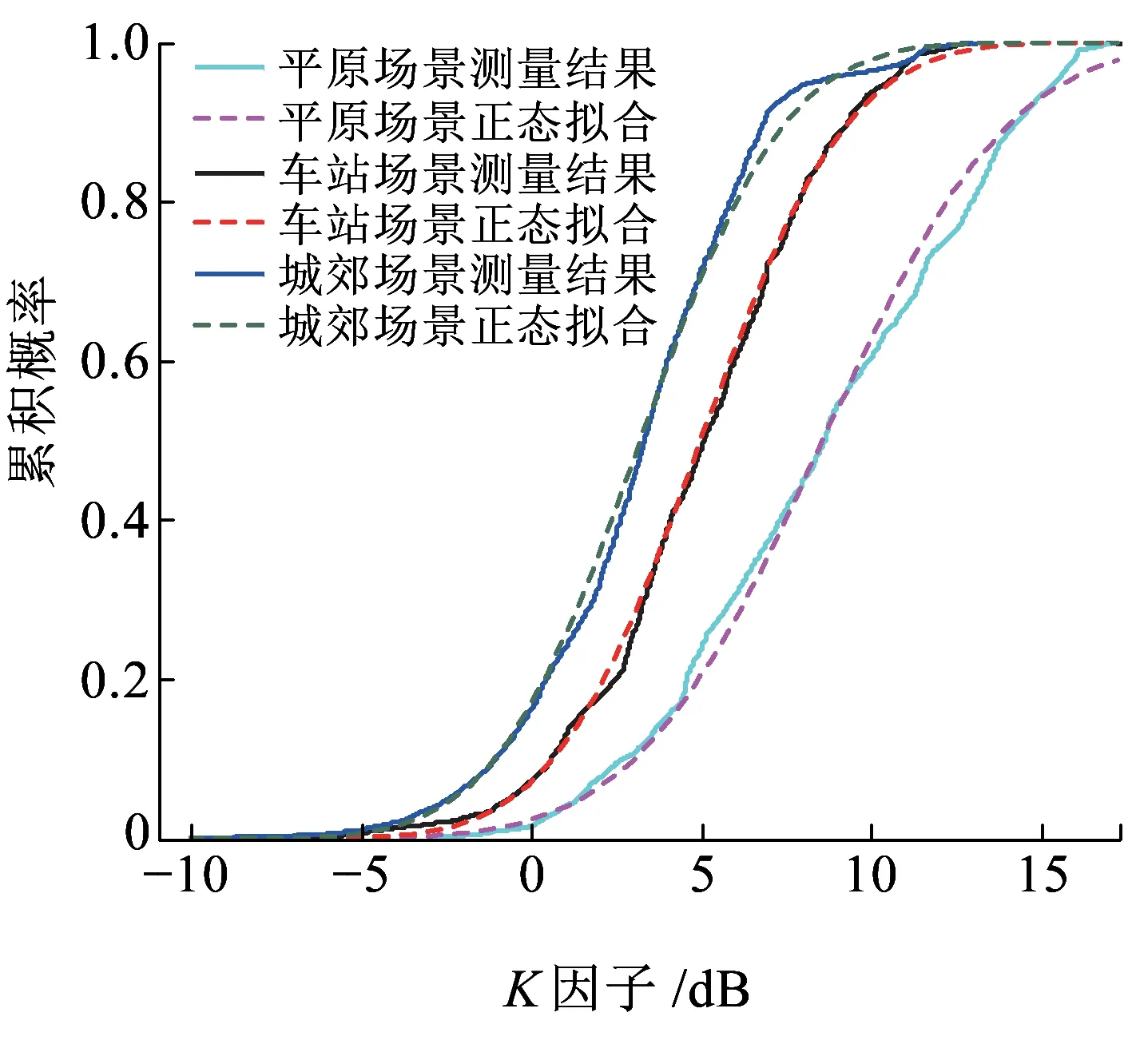
图5 莱斯K因子测量结果

图5中实线和虚线分别代表着根据实际测量的和根据累计分布函数拟合的两种结果，其中城郊场景、车站场景、平原场景对应的曲线分别是左侧、中间和右侧。由图5可知，这3个场景下的莱斯K因子的累积分布都能较好地拟合正态分布，其中城郊、车站和平原环境下的莱斯K因子的标准差分别为3.35，3.40和4.33 dB。在城郊场景中，莱斯K因子的值相对最小，其平均值约3.20 dB。在车站场景中，莱斯K因子的值介于城郊和平原之间，其平均值约为4.98 dB。在平原场景中，莱斯K因子的值最大，其平均值约为8.56 dB。这是因为在城郊环境中，居民区中建筑物较多，传播环境中的散射体丰富。在平原环境中的多径分量较少，而在车站环境下，多径分量介于以上二者之间，因此K因子的平均值介于二者之间。虽然车站周围的散射体较少，但从实际的测量结果来看，该区域的多径分量还是比较丰富，这是由于车站内部相对封闭的结构造成的。

2.2 时延扩展

在多径传播环境下，存在不同传播路径、传播时间的信号分量，因此会产生时延扩展。主要参数有平均时延扩展和RMS时延扩展。

时延扩展的定义与功率时延谱PDP(Power Delay Profile)有关。功率时延谱函数是基于固定时延参考量的附加时延[14]。

( 1 )

式中：h(t,τ) 为时变信道中的冲激响应；trep为信道中冲激响应取值周期；Δτ为时延扩展的分辨率；l为时延扩展中可分辨的数目；itav为时间标，与地理位置对应；W为统计冲击响应的平均窗口宽度，一般取20个波长内的信道快照。平均时延扩展定义为[15]

( 2 )

式中：ak为第k条多径的衰减因子；P(τk)为在时延点τk上多径衰落的相对功率。RMS时延扩展定义为

( 3 )

( 4 )

根据以上RMS时延扩展公式，分别计算平原、车站和城郊环境的RMS时延扩展。在平原环境中，RMS时延扩展的值最小，平均值约为40.4 ns；车站环境中，RMS时延扩展的值介于平原和城郊环境之间，平均值约为146.5 ns，与文献[16]中计算的RMS时延扩展结果131.1 ns基本一致；城郊环境中RMS时延扩展的值最大，平均值约为312.7 ns。对比三种场景下的RMS时延扩展均值，平原场景下最小，车站场景次之，城郊场景下最大，与多径分量的变化趋势相同，与莱斯K因子的变化趋势相反。图6为3个场景下RMS时延扩展的CDF对比图。

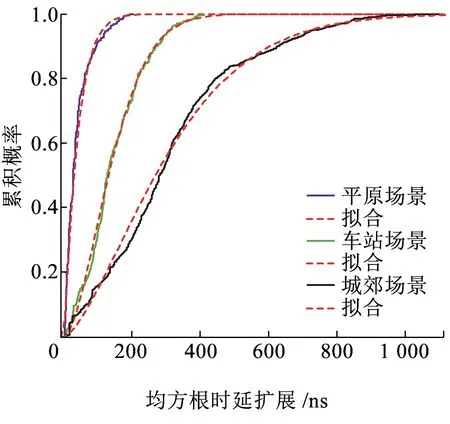
图6 RMS DS测量结果

根据图6，对城郊环境中RMS时延扩展的测量结果进行分析，最大值约为1 000 ns，其中26%的值大于400 ns，70%的值大于200 ns。在车站场景下，RMS时延扩展的最大值不超过400 ns，70%以上的RMS时延扩展集中在200 ns以内，90%以上的RMS时延扩展集中在300 ns以内。在平原场景下，RMS时延扩展均在200 ns以内，90%以上的RMS时延扩展集中在100 ns以内。

图6中红色虚线满足Weibull分布，这是K因子的累积分布函数拟合结果。Weibull分布可以表示为

( 5 )

式中：x为随机分布；λ参数表示比例；k参数表示形状。表2给出了平原、车站和城郊环境中的Weibull分布参数。

表2 Weibull分布参数

2.3 到达角

高速铁路中列车沿铁轨行驶时，忽略基站到铁轨的距离，根据以下简化的几何模型，可以求出接收信号直射径的到达角AOA(Angel of Arrive)为

( 6 )

假设基站位于该段铁轨的中间，其覆盖铁轨是有一定的范围的，D为覆盖长度，v为行驶速度，t为行驶时间，当t为0时表示列车刚运行到信号的覆盖范围内，当t为t0时表示列车运行到信号覆盖范围边缘的时刻，H为基站高度，这里取35 m。

在一般情况下，计算到达角使用的方法为ESPRIT算法[17]，主要通过接收信号的协方差矩阵，通过构造旋转不变子空间，进行特征值分解并估计信号到达角。使用此算法的难度在于需要用多根天线构成天线子阵进行数据接收。而本文采用一种移动虚拟天线阵列的策略[18]，此方法模拟多天线阵列只需要单根天线。基于ESPRIT算法进行改进，可以得到3种常用算法，包括最小二乘LS(Least Square)ESPRIT、整体最小二乘TLS(Total Least Square)ESPRIT以及Unitary ESPRIT算法，在文献[19]中有具体介绍。在本文的实际测量中，使用SCM模型，通过不同的算法计算信号到达角，并比较这三种算法的误差值。根据结果分析，TLS ESPRIT和Unitary ESPRIT算法的性能较LS ESPRIT好，当信噪比较低时，Unitary ESPRIT算法性能稍好于TLS ESPRIT。此外，Unitary ESPRIT算法的计算复杂度相对较低。通过以上比较，本文选择Unitary ESPRIT算法。

由两种方法得到的三种场景下到达角估计如图7所示，实线表示的信号到达角是通过模型得出的，蓝色表示的信号到达角是通过Unitary ESPRIT算法得出的。车站环境中，实际车站的位置位于时间范围7～15 s内。如图7所示，在平原、车站和城郊环境下，信号到达角的变化趋势大致相同。在城郊和车站环境中信号到达角波动较大，这是因为散射体比较丰富，多径分量较多，而平原场景下，信号到达角的变化相对稳定。

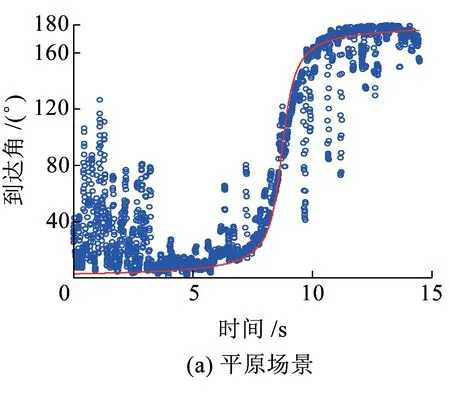
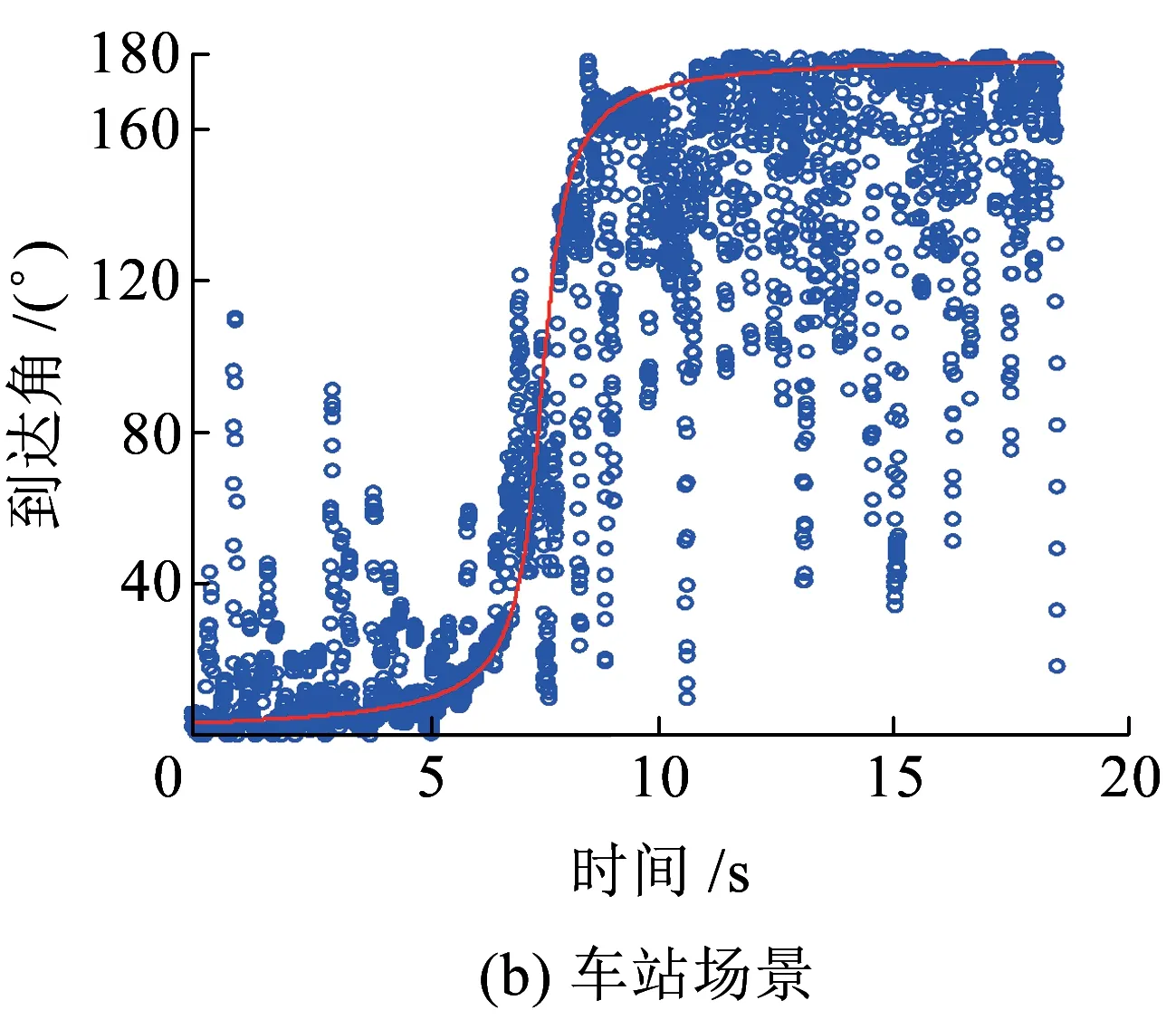
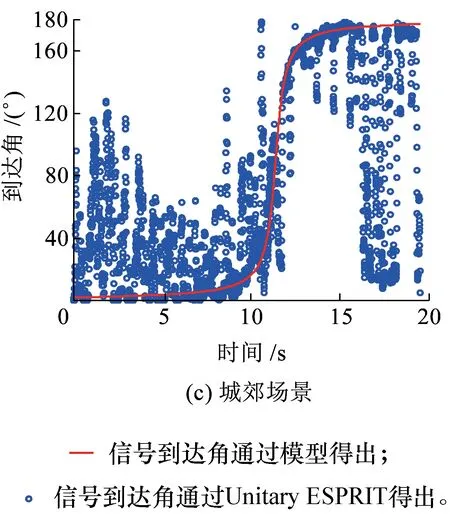
图7 到达角测量结果

2.4 功率角度谱

在任意时刻都存在来自不同方向的多径信号，功率角度谱可以描述这些信号的功率分布情况和角度特性。设t时刻的功率角度谱为P(t,θ),则有

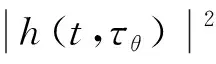
( 7 )

式中：τθ表示到达角为θ的多径分量的时延。本文选择3个不同时段的平均功率角度谱来描述功率角度谱的变化趋势，第一时段是列车经过基站前，第二时段是列车经过基站附近，第三时段是列车经过基站后，3个时段是列车从接近基站到远离基站的过程。

图8为平原场景下的功率角度谱的变化图。由图8可知，平原场景下的功率角度谱变化明显。列车在靠近基站时，0°～60°内的到达波贡献了主要的接收信号能量；列车在基站附近时，60°～120°内的到达波贡献了主要的接收信号能量；列车远离基站时，120°～180°内的到达波贡献了主要的接收信号能量。

图9描述了车站场景下，当列车运行到基站附近时的功率角度谱。由图9可知，在0°～180°内分布着大部分信号。因为在车站场景下，列车运行到基站附近，多径数量较多，几乎各个角度都有。本文并未给出列车未到达车站和远离车站时的功率角度谱图，因为在这两种情况下，列车没有位于车站场景，并且处于平原场景下，功率角度谱趋势和平原场景下的基本一致。

在城郊场景下，由于散射体丰富，列车靠近基站、在基站附近或远离基站3种情况下，各个角度均可以接收到信号功率，多径分量在几乎每个时刻都存在。所以本文未给出城郊场景下的功率角度谱图，其功率角度谱与图9类似。

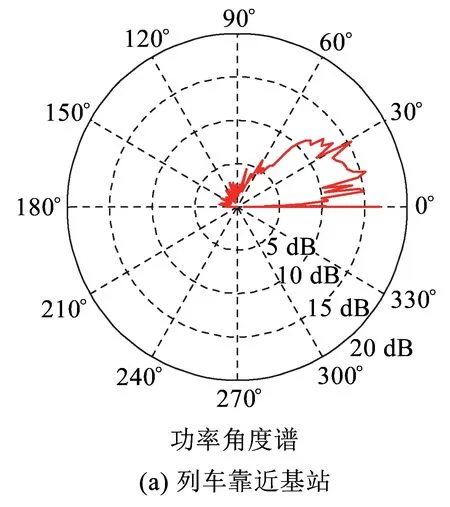
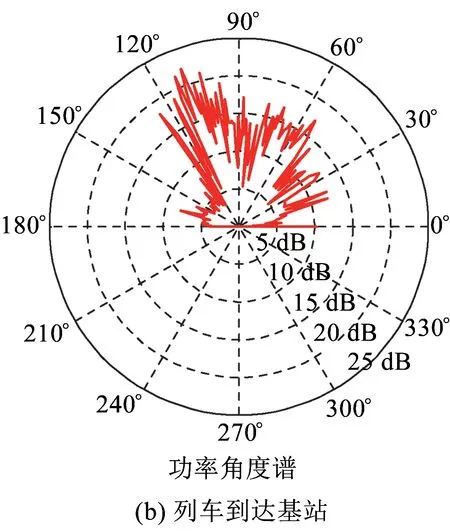
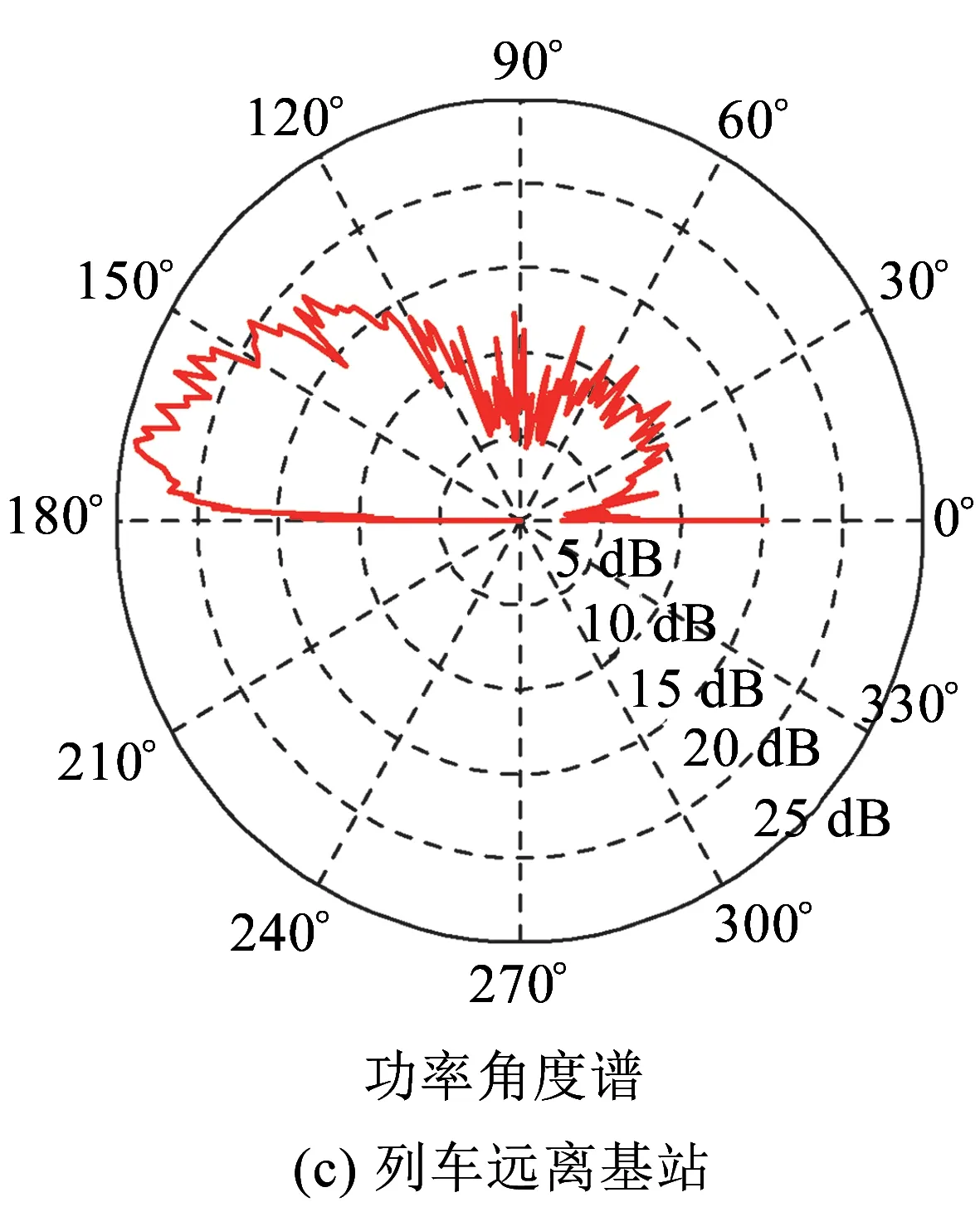
图8 平原场景下功率角度谱测量结果

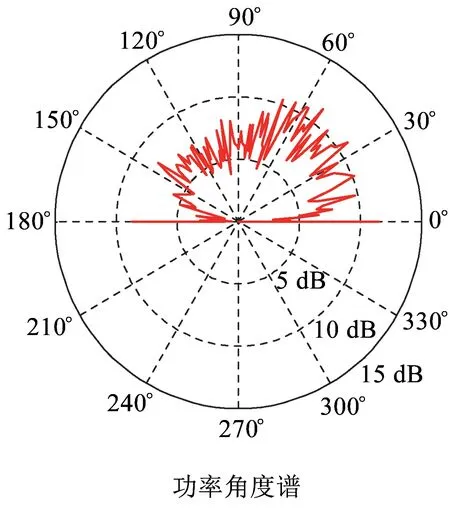
图9 车站场景下功率角度谱测量结果

3 非平稳特性分析

3.1 稳态间隔

高速移动环境下的无线信道并不是平稳的，也就是说，信道不具备广义平稳非相关散射WSSUS (Wide Sense Stationary Uncorrelated Scattering)特性[20]。稳态间隔用来描述信道能够保持WSSUS特性的有效范围，可以基于信号功率的相关性描述稳态间隔，在文献[21]中对这种方法进行了具体的介绍，定义功率相关系数为

( 8 )

其中

( 9 )

式中：h(xm)为xm处冲激响应；N为功率窗长。

定义xk处的稳态间隔Ik为

Ik=(kmax-kmin)Δx

(10)

其中

(11)

(12)

式中：L为处理数据的长度；cthreshold为提前设置的相关系数，在计算中，cthreshold取值分别为0.7、0.8、0.85。

在3种场景下，稳态间隔的累积分布函数曲线如图10所示。由图10可知，同一场景下，cthreshold取值越大，稳态间隔越小。在取值相同时，平原场景下的稳态间隔最大，车站次之，城郊最小。因为平原场景下信道衰落的一致性较高，移动环境变化较小。城郊环境下，障碍物较多，同一时刻来自不同方向的多径信号丰富，造成信道衰落不一致。在车站环境中，信道衰落的变化介于以上二者之间。此外，当cthreshold取值越来越大时，3个场景下的稳态间隔值也越来越接近。表3给出了各个场景下取不同相关系数时的稳态间隔均值。

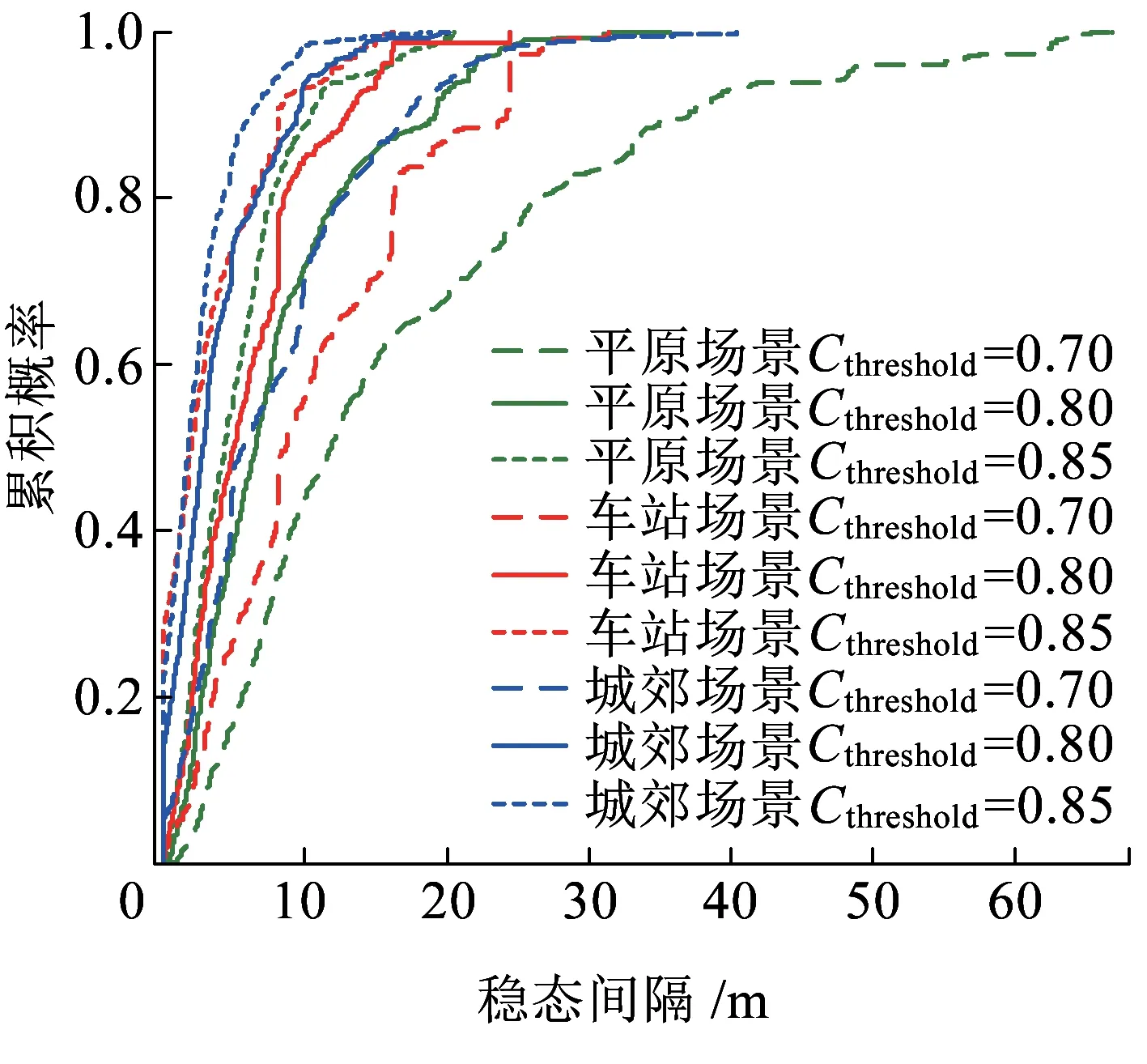
图10 稳态间隔的CDF比较

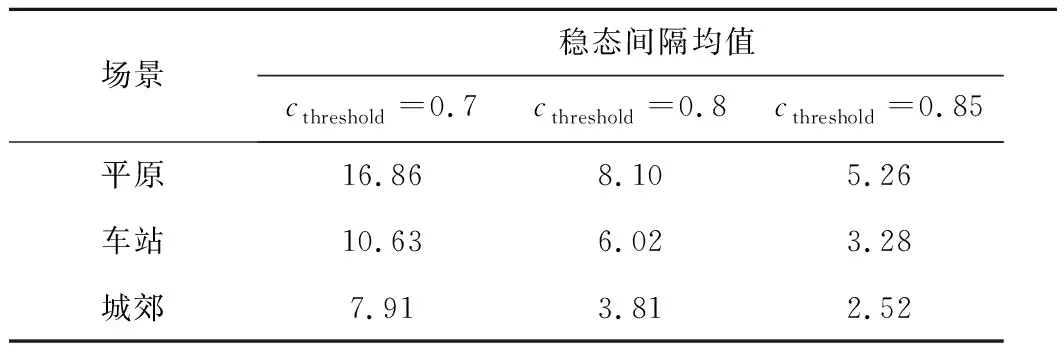
表3 稳态间隔的均值比较 m

3.2 多径的动态变化

不同地区的环境是不同的，当列车移动时，接收信号中的多径分量也不是一成不变的，为了描述这种动态变化，本文使用了一种有限状态的马尔科夫链模型。

和文献[22]一样建立马尔科夫模型，设模型的状态空间为E，则E={S0,S1,S2,S3}，其中：S0表示下一状态时多径分量的数量没有发生变化，没有新的多径分量，也没有多径分量消失；S1表示下一状态时新的多径成分变多，但没有多径成分消失；S2表示下一状态时一部分多径成分消失，但没有新的多径成分；S3表示下一状态时新的多径成分变多，同时也有一部分多径成分消失。

状态描述是指多径的变化情况，并且是下一时刻相对于当前时刻的变化。各个状态在列车运行过程中发生转化，并且最新时刻的状态只与它前面时刻的状态相关。设转移概率Pij表示从状态Si变为状态Sj的可能性大小，其中0≤i,j≤3，则对应的状态转移情况如图11所示。

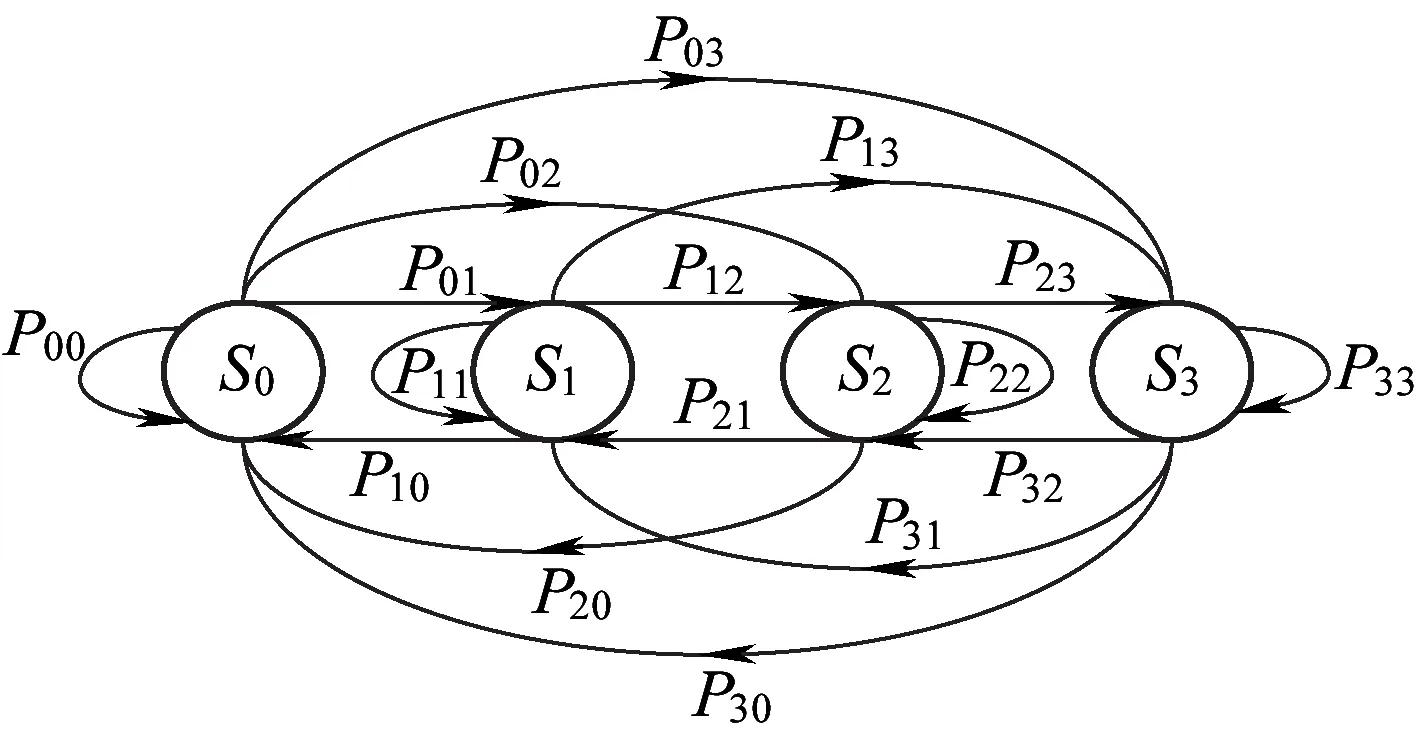
图11 状态转移

对应的状态转移矩阵P为

(13)

0≤pij≤1i,j=0,1,…,N-1

(14)

(15)

式中：N为马尔科夫链中的状态数，此处N=4，相应的稳态概率为

(16)

满足条件

PS0+PS1+PS2+PS3=1

(17)

在3种环境下，最终得到的结果Pplain、Pstation、Psuburb为

分析Pplain、Pstation、Psuburb，根据以上结果可知，在平原环境中：

(1)若目前处于状态S0，下一状态最可能转化为状态S0。表示在这种时刻附近，列车周围的环境变化不大，多径分量的数量没有发生变化。

(2)若目前处于状态S1，下一状态最可能转化为状态S2。表示目前有新的多径成分变多，但是下一状态最有可能有一部分多径成分消失。因为在平原环境中建筑物较少，影响多径分量的物体较少，所以下一状态消失的多径成分，很有可能就是目前产生的新的多径成分。

(3)若目前处于状态S2，下一状态最可能转化为状态S1。表示目前有一部分多径成分消失，接下来也会有新的多径成分产生。

(4)若目前处于状态S3，下一状态最可能没有发生转化，因为当前环境下有比较多的散射体。

在车站场景和城郊场景下，当前时刻无论处于哪种状态，下一时刻最有可能是S3状态。无论何时，当有一部分多径成分消失时，也有一部分多径成分产生，这种消失和产生同时发生的情况是最可能出现的。这是由于这两种环境下散射体较多引起的。

马尔科夫链的平稳分布可以由状态转移矩阵得到。在平原、车站和城郊环境中的平稳分布为

由稳态概率矩阵可知，无论在哪种环境下，最有可能处于S3状态。在平原环境中由于散射体较少，处于S1、S2状态和处于S3状态的可能性大致相同。但是在车站、城郊场景中，由于环境中散射体较多，处于S3的概率远大于其他3种状态。但是无论在哪种环境下，由于接收信号中多径的出现和消失是对等的，处于S1和S2状态的稳态概率都大致相等。

4 结束语

本文基于信道实测数据，对比分析了3个高铁场景即平原、车站、城郊下的信道小尺度衰落特性和非平稳特性。分析结果表明，在平原环境中，莱斯K因子和稳态距离最大，车站次之，城郊环境下最小，而RMS时延扩展正好与此相反。平原场景下，功率角度谱基本随着列车接近与远离基站而变化，而在车站和城郊场景下，无论列车靠近还是远离车站，功率几乎在各个角度都有分布。建立的马尔科夫链模型表明，在多径丰富的车站和城郊环境中，保持S3状态的可能性要远大于其他状态。