巧用三角板学习正方形

王彩霞

摘 要：用全等三角板做教具学习正方形，简洁，直观，激发学生学习兴趣，培养学生观察、思考、归纳总结等数学能力。

关键词：全等三角板;拼图;正方形;性质

正方形是一个特殊的平行四边形。特殊在哪儿呢？首先它是一个平行四边形，其次，它同时具备菱形、矩形的性质。在正方形的教学中，我用三角板做教具，直观简洁，极大地缩短了学生知识内化的过程。

一、导入

提问：

③什么是平行四边形？②平行四边形有哪些性质？

③如何判定一个四边形是平行四边形？用同样的方式提问矩形的定义，性质和判定;菱形的定义，性质和判定。

在提问的同时，我分别拿出全等三角形拼成平行四边形、矩形、菱形。（如图）让学生结合图形，利用数形结合的方式，回憶，思考并回答问题。（这样做的好处，一方面温习了旧知识，另一方面对新知识的学习做了所铺垫.）

二、新知探究

我分别用两个全等的等腰直角三角板和四个全等的等腰直角三角板拼接成两个正方形，如图：提问：我手中的图形是什么？学生集体回答：是正方形。提问：你怎么知道它是正方形？学生回答：看到的。追问：你看到的就是真的吗？

你能正明它就是正方形吗？

学生1：图1中，红色三角板和绿色三角板是全等的等腰

直角三角形，所以，他们的四条边都相等，四个角都是直角。四条边都相等，且四个角都是直角的四边形，是正方形，所以，图1是正方形。

学生2：图2是由四个全等的等腰直角三角形拼接而成，所以，四条边都相等，四个角都是两个四十五度角的和，即都为九十度。所以图2也是正方形。

然后我让小组内用同样的方法拼接正方形，并探究：

问题一：正方形的性质是什么？（小组内观察、探究、归纳） ;交流：叫学生在黑板上自己写出探究出来的性质。边上的关系：两组对边平行且相等，四条边都相等

我引导学生思考总结：“两组对边平行”——平行四边形的定义，所以它是特殊的平行四边形。“四条边都相等”——菱形的定义，所以它又是特殊的菱形。

让学生证明：生1：图1中，因为内错角相等，都是45度，所以两组对边平行。（图2略）生2：因为图1、图2中，正方形都由全等的等腰直角三角形拼接而成，所以正方形的四条边都相等。

问题二：正方形的角、对角线各有什么关系？角上的关系： 对角相等，四个角都是直角。继续引导思考并总结：“对角相等”——平行四边形角上的性质。“四个角都是直角”——矩形角上的性质，所以正方形也属于矩形。对角线上的关系：对角线互相平分。（平形四边形的性质）：对角线相等。（矩形的性质）：对角线互相垂直。（菱形的性质）：每条对角线平分一组对角。提问：你是怎么发现对角线上有这些性质呢？

学生1回答：因为图2是由四个全等的等腰直角三角形拼接而成，并且八条直角边都交于一个点，所以对角线相等，互相平分且垂直。学生2回答：因为图2是由四个全等的等腰直角三角形拼接而成，四个直角都是由两个四十五度的角构成，所以每条对角线平分一组对角。

三、课堂小结

集体回顾总结：正方形是一个特殊的平行四边形，特殊的矩形，特殊的菱形，所以具有这些图形所具有的所有性质。 给学生一分钟的时间，对性质进行理解和记忆。

四.练习巩固：

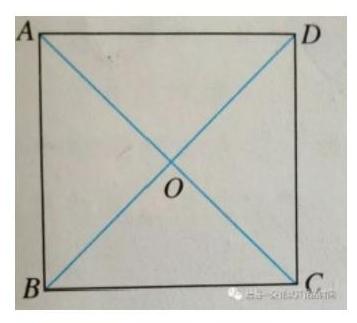
已知四边形ABCD是正方形，对角线AC，BD相交于点O.求证：△ABO，△BCO，△CDO，△DAO是全等的等腰直角三角形。

我先让学生自己读题思考，然后叫学生讲解自己的思路，我再加以提点，最后学生自己到黑板上演题。等学生们做完，我就学生做题情况进行订正点拨。

学生证明：∵四边形ABCD是正方形∴AC=BD，AC⊥BDAO=BO=CO=DO

在△AOD和△AOB中AO=AO∠AOD=∠AOBDO=BO∴△AOD≌△AOB   （SAS）同理△AOD≌△COD，△BOC≌△AOB△BOC≌△DOC

∴△AOD≌△AOB ≌△BOC≌△DOC学生的证明过程很完整，思路也比较清晰，但是过程不是很简洁。简洁过程如下：

证明：∵四边形ABCD是正方形∴AC=BD，AC⊥BDAO=BO=CO=DO

∴△AOD，△AOB，△BOC，△DOC都是等腰直角三角形

∴△AOD≌△AOB ≌△BOC≌△DOC

五：反思

一节课就这样很轻松地讲完了。我觉得用这种方法给学生讲课，简洁直观，对学生的理解和记忆有很大的帮助，更重要的是激发了学生学习的积极性。