模型建立与算法构造：基于Prim算法构造最小生成树

李琳 赵娟 虎建勋

摘 要 最小生成树有许多重要的应用。例如：要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。本文通过使用Matlab软件进行编程实现了用Prim算法构造最小生成树的分析运算。本程序可以方便地处理层次分析法下较大的运算量，解决层次分析法的效率问题，提高计算机辅助决策的时效性。其中建立了有效的基于Prim算法的数学模型并验证了模型的合理性和科学准确性。利用MATLAB、EXCEL、SPSS13.0 for windows等软件，实现了高效、准确的研究。

关键词 模型 atlab软件 算法构造

中图分类号：TP312文献标识码：A

1建立结构模型

1.1最小生成树相关概念

连通图：任意两个结点之间都有一个路径相连。

生成树（Spannirng Tree）：连通图的一个极小的连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。

最小生成树（Minimum Spannirng Tree）：连通图的最小代价的生成树（各边的权值之和最小）。

最小生成树即对于连通的带权图（连通网）G，其生成树也是带权的。生成树T各边的权值总和称为该树的权，记作：这里：TE表示T的边集，w（u，v）表示边（u，v）的权。权最小的生成樹称为G的最小生成树（Minimum SpannirngTree）。最小生成树可简记为MST。

1.2 Prim算法实现

Prim算法是一种贪心算法，将全部的顶点划分为2个集合，每次总在2个集合之间中找最小的一条边，局部最优最终达到全局最优，这正是贪心的思想。在无向加权图中，n个顶点的最小生成树有n-1条边，这些边使得n个顶点之间可达，且总的代价最小。

Prim算法的每一步都会为一棵生长中的树添加一条边，该树最开始只有一个顶点，然后会添加个边。每次总是添加生长中的树和树中除该生长的树以外的部分形成的切分的具有最小权值的横切边。

设置两个集合P和Q，其中P用来存放Q的最小生成树中的顶点，集合Q存放G的最小生成树的边。令集合P的初值为P={V1}（假设构造最小生成树时，从顶点V1出发），集合Q的初值为Q= 。Prim算法的思想是，从所有的边中，选取具有最小权值的边PV，将顶点V加入集合Q中，如此不断重复，直到P=V时，最小生成树构造完毕，这时集合Q中包含了最小生成树的所有边。

Prim的算法如下：

2案例分析

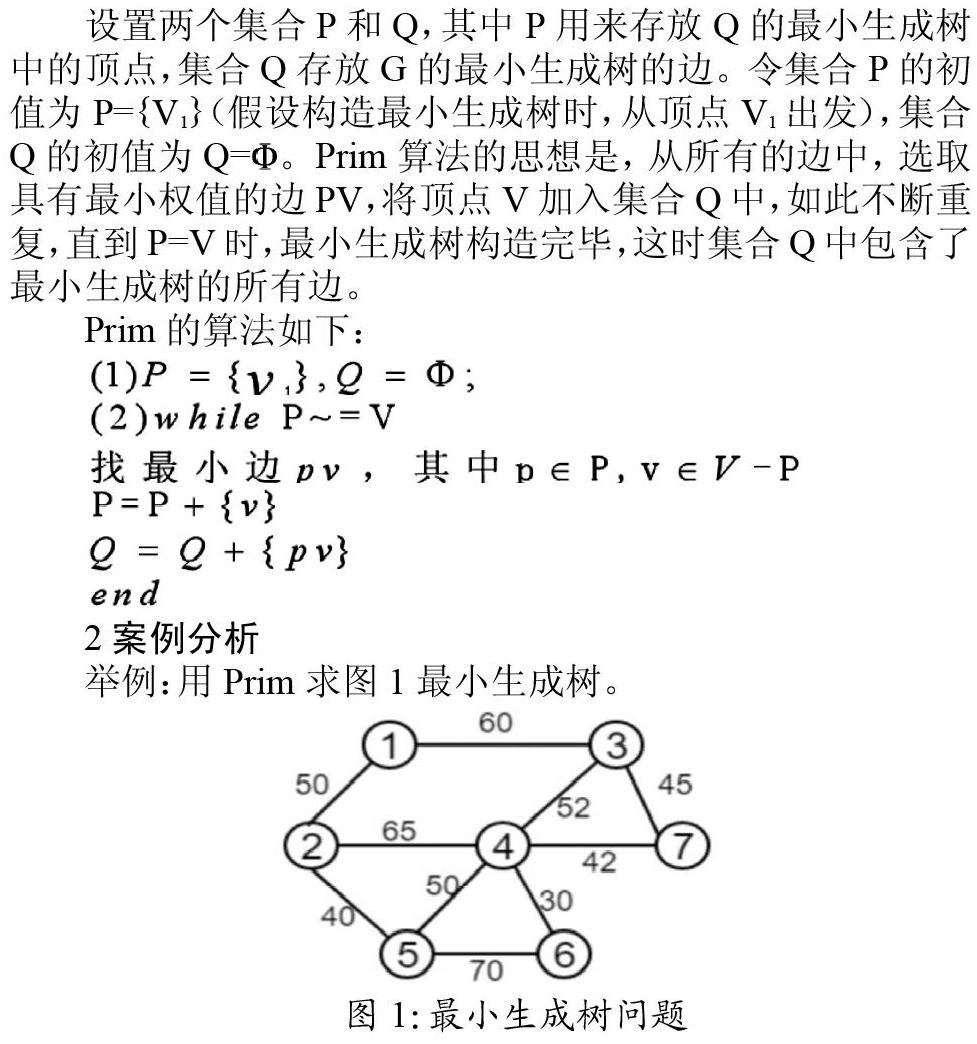
举例：用Prim求图1最小生成树。

用的第一、二、三行分别表示树的起点、终点、权集合。MATLAB 程序如下：

clc;

clear;

a=zeros（7）;

a（1，2）=50;a（1，3）=60;

a（2，4）=65;a（2，5）=40;

a（3，4）=52;a（3，7）=45;

a（4，5）=50;a（4，6）=30;a（4，7）=42;

a（5，6）=70;

a=a+a';a（find（a==0））=inf;

result=[];p=1;tb=2;length（a）;

while length（result）～=length（a）-1

temp=a（p，tb）;temp=temp（：）;

d=min（temp）;

[jb，kb]=find（a（p，tb）==d）;

j=p（jb（1））;k=tb（kb（1））;

result=[result，[j;k;d]];p=[p，k];tb（find（tb==k））=[];

end

Result

计算结果如图2所示：所以由结果可得起点为1，终点为2，权集合为50。很明显对于每个节点（初始节点除外），都要进行此次遍历查找距离树最近节点O（n），和一次更新操作O（n），所以总的时间复杂度为O（n^2）。

参考文献

[1] 严蔚敏.数据结构预算法分析[M].北京：清华大学出版社，2011.

[2] 刘来福，曾文艺.数学模型与数学建模[M].北京：北京师范大学出版社，1997.

[3] 王周宏.运筹学基础[M].北京：清华大学出版社，北京交通大学出版社，2010.

[4] 徐全智，杨晋浩.数学建模[M].高等教育出版社，2004.

[5] 姜启源，谢金星等.数学模型（第三版）[M].高等教育出版社，2004.

[6] 程杰.大话数据结构[M].清华大学出版社，2011.

[7] 梁西陈.最小生成树在网络设计中的应用[J].宿州教育学院学报，2008（11）.

[8] 王新奇.最小生成树算法及其应用[J].西安文理学院学报，2009（12）.