基于林木多期直径测定数据的异龄林年龄估计方法Ⅱ
龙时胜,曾思齐,甘世书,肖化顺,刘 洵,向博文
(1.中南林业科技大学,湖南 长沙 410004;2.国家林业局中南林业调查规划设计院,湖南 长沙 410014)
异龄林是由不同年龄、不同径级的林木在同一立地上组成的一个生态系统。据第八次全国森林资源连续清查统计[1],我国异龄林面积达1.218 4×105hm2,异龄林蓄积达122.96×109m3,异龄林作为我国森林资源的主体[2],在发挥生态效益、维持物种多样性等方面起着重要的作用。目前我国对于异龄林的研究主要集中在空间结构[3-4]、立地质量评价[5]以及经营择伐技术[6]等方面,由于异龄林内部年龄结构和直径结构等的复杂性,我国对异龄林的经营还未形成一套系统的方案。
林分年龄是研究林分生长动态[7]、林分生物量变化[8]以及立地质量的重要基础。随着林分年龄的变化,林分生长往往呈现一定的规律性,例如林分年龄越大,林木的生长速率越高[9]。同时,森林净初级生产力也随着林分年龄的变化表现出一定的规律[10],如阔叶混交林的净初级生产力在林分年龄较小时达最大,而针叶林的净初级生产力在林分年龄较大时达最大[11]。林分年龄对于碳储量的分布也存在一定影响,如林分碳储量随着林龄的增大而增加[12],且不同林龄的林分在林地生产力、碳储量以及土壤养分方面均存在一定的差异性[13]。林分优势木年龄是编制地位指数表的基础,但其研究对象往往是同龄林,利用林分优势木年龄与优势木平均高编制异龄林地位指数表的研究较少,其原因一方面是异龄林内部结构复杂,另一方面则是异龄林的年龄获取难度较大,因此,构建有效方法来估算异龄林的林分年龄至关重要。
林分年龄包括同龄林与异龄林年龄,同龄林内部结构简单,其年龄的获取难度较小,而异龄林林分内部直径与年龄结构复杂,其年龄的获取难度较大。目前,遥感已被证明是一种能有效估算出林分年龄的工具,利用时间序列遥感数据能有效地估算林分年龄[14-15],然而,目前最长时间序列的陆地卫星数据只能追溯到1972年,且许多地区缺少此类数据或质量较差。
在林分调查中,胸径是较容易获取且准确度较高的林木测量因子,且我国的森林资源连续清查工作是每间隔5年进行一次的全国森林资源调查工作,大部分固定样地的林木胸径数据均存在6期(30 a)以上的重复测量数据,因此本文的目的是基于林木多期直径测定数据,提出一种估计异龄林林分平均年龄的新方法。
1 研究区概况
研究区青石冈国有林场位于湖南省东南部,地处罗霄山脉中段,位于113°34′45″~114°07′15″E,26°03′03″~26°38′30″N,海拔分布在165.4~2 115.4 m,年平均气温17.3 ℃,年平均降水量1 496.7 mm。林场内土壤垂直带谱明显,海拔350 m 以下以红壤为主,350~650 m 为山地黄红壤,650~800 m 为山地黄壤,800~1 200 m为黄棕壤,1 200~1 700 m 为暗黄棕壤,1 700 m以上为山地草甸土。林场内的主要优势种群为木荷-针叶混交林,栎类常绿阔叶林等。
2 材料与方法
2.1 材料来源

图1 青石冈林场地理位置Fig.1 Geographical location of Qingshigang forest farm
研究样地设置于2003年,面积为20 m× 20 m,对样地内胸径≥5 cm 的林木进行每木检尺,主要测量胸径、树高、冠幅、第一枝下高,以及每株林木的相对坐标位置,并采用生长锥测定每株林木的年龄。以后每隔3年进行一次复测工作,截止2015年,共进行了5 次,样地的基本概况见表1。

表1 样地的基本概况Table 1 Basic information of the sampling plot
2.2 研究方法
研究提出的异龄林林分平均年龄估计方法,应用对象为具有多期直径测定数据的异龄林林分,具体估计方法如下。
2.2.1 确定各树种的年龄变异范围
相同立地条件下,同一树种相同直径的林木由于受到相邻木的竞争影响,其年龄往往表现出一定的差异性。被压木为林分内生长速率较慢的林木,优势木为林分内生长速率较快的林木[16],相同直径的被压木与优势木,其年龄差异性可能较大。为确定林木相同直径的年龄变异范围,可利用林木相对直径法[17]在林分内选取一株被压木与一株优势木进行树干解析,采用Richards[18]生长方程模拟2 株林木的直径生长过程,其直径生长方程可表达为:

式中:D压为被压木的直径;D优为优势木的直径;A压为被压木的年龄;A优为优势木的年龄;a,r,c 为模型参数。
模型(1)和模型(2)中因变量为直径 D压、D优,自变量为年龄A压、A优,表示林木直径随年龄的变化趋势。而研究是为了解相同直径的年龄变异范围,因此求解模型(1)和模型(2)的反函数,模型表达式转换为:

由模型(3)和模型(4)可知,相同直径林木的年龄变异范围为(A优,A压),该变异范围可表示为同一立地条件下,相同直径林木的年龄范围在A优与A压之间。
2.2.2 确定林木的初始年龄
在林分的多期调查数据中,林木的直径容易获取,而林木的年龄获取难度较大,调查初期林木的年龄是未知的,调查第二期林木的年龄为调查初期的年龄+调查间隔期h,调查第三期林木的年龄为调查初期的年龄+2 倍调查间隔期h,以此类推,调查第n 期林木的年龄为调查初期的年龄+(n-1)倍调查间隔期h(每次的调查间隔期h 相等)。因此,只要知道林木调查初期的年龄,即可知林木在各期的年龄。在现实工作中,林木调查初期的年龄可以采用树干解析、生长锥或生长曲线的方法获取,但获取难度大且成本较高。因此,研究提出一种对年龄取随机值的方法来确定林木调查初期的年龄,具体为:依据调查初期各林木的直径大小,利用Excel 中的Randbetween 函数为各株林木在年龄变异范围(A优,A压)内取随机值,即Ai=(Ai优,Ai压),其中Ai为第i 株林木调查初期的年龄,Ai优为第i 株林木对应直径的最小变异年龄,Ai压为第i 株林木对应直径的最大变异年龄,h 为调查间隔期。
2.2.3 林分直径与年龄信息的获取及生长方程的拟合
利用随机取值的方法获取调查初期各株林木的年龄后,各株林木调查初期的直径与年龄信息即为(D1i,A1i),各株林木第二期的直径与年龄信息即为(D2i,A1i+h),各株林木第三期的直径与年龄信息即为(D3i,A1i+2h),以此类推,各株林木第n 期的直径与年龄信息即为[Dni,Ani+(n-1)*h],由此林分内所有林木在各调查期的直径与年龄信息都已知,利用Richards 生长方程D=f(A)即可模拟出该林分平均直径随平均年龄的变化趋势,再对该生长方程求反函数A=f(D),即可求出该林分平均年龄随平均直径的变化趋势。由于林木初始年龄采取随机函数的方法进行赋值,每一次随机取值,其初始年龄可能都会存在差异性,为尽量减少年龄估算的误差,研究考虑对林木的初始年龄进行10 次随机取值,由此可能生成10 组不同的直径与年龄信息,并且生成10 个不同参数的生长方程,如生成的其中2 组直径与年龄信息见图2。
2.2.4 林分年龄的测定

图2 林木直径与年龄信息分布示意图Fig.2 Distribution diagram of the tree diameter and age information
异龄林林分内直径分布一般呈倒“J”型曲线,中小径阶林木占多数[19],利用算术平均方法计算异龄林林分平均年龄时,可能会导致林分平均年龄偏低,因此采用断面积加权平均的方法计算异龄林林分平均年龄。已知该林分年龄与直径的关系A=f(D),利用断面积加权平均的方法计算出该林分的断面积加权平均直径Dg,将Dg 代入方程A=f(D),即可求出该异龄林林分的平均年龄Ai,其中Ai表示一次随机取值所求得的林分平均年龄,为保证估计结果的准确性,分别利用10 个不同参数的生长方程计算林分的平均年龄Ai,最后取林分平均值=
2.2.5 年龄估计效果的验证
在样地第一期调查时,林木年龄已经利用生长锥获取,利用断面积加权方法可求出该林分在各调查期的真实平均年龄Ai。利用本研究提出的方法同样可拟合出该林分在各调查期的估计平均年龄。采用绝对误差、相对误差、平均绝对百分误差三个评价指标对年龄估计方法进行检验,三个评价指标数值越小,说明估计效果越好,具体计算公式如下:
式中:Ai为第i 个实测值;为Ai的预测值,N为样本数。
3 结果与分析
3.1 各树种的直径变异范围
利用林木相对直径法在样地内分树种选取优势木与被压木各1 株,对6 株林木进行树干解析,采用Richards 生长方程分别模拟6 株林木的直径与年龄生长过程,结果见表2。

表2 优势木与被压木的生长方程拟合结果Table 2 The fitting results of the growth equation of dominant wood and pressed wood
由表2可知,6 个生长方程的均方根误差(RMSE)均在0.6 以下,R2均在0.97 以上,拟合效果好。对被压木与优势木的生长方程求反函数,结果为:

由模型(5)~(10)可知,木荷在该立地条件下的年龄在各直径的变异范围为:[-7.46*ln(1-(D/20.06)0.371),-17.24*ln(1-(D/26.78)0.381)],马 尾 松在该立地条件下的年龄在各直径的变异范围为:[-8.55*ln(1-(D/15.32)0.478,-6.41*ln(1-(D/10.01)0.326)],杉木在该立地条件下的年龄在各直径的变异范围 为:[-10.75*ln(1-(D/21.04)0.587),-10.53*ln(1-(D/12.20)0.576)],各树种的年龄变异区间见图3。
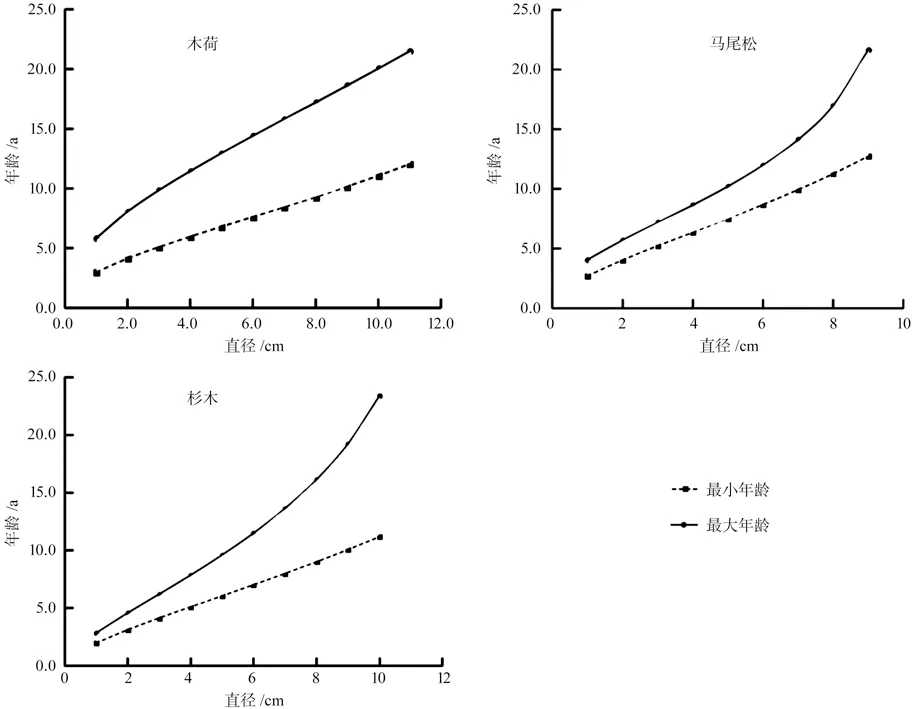
图3 3 个树种的年龄变异范围Fig.3 The age range of the three species
由图3可知,各树种在对应直径下的年龄差异随着林木直径的增大而增加,说明林木生长初期由于所需的营养空间较少,林木生长受到的竞争压力较小,其直径与年龄的差异性较小;随着林木直径增大,所需营养空间增加,林木与周边林木的竞争加剧,其直径与年龄的变异程度增加。
3.2 各树种直径与年龄信息的获取
依图3所示的各树种年龄变异范围,利用Excel 中的Randbetween 函数“=randbetween(最小年龄,最大年龄)”,对样地中各树种第一期的年龄取随机值,林木第二至第五期的年龄分别为第一期年龄加(n-1)倍调查间隔期,3 个树种五期的年龄赋值结果见表3~表5。
由表3~表5可知,依据各树种的年龄变异范围,对林木初始年龄进行随机取值时,相同直径的林木年龄表现出一定的差异性。如表3中,木荷直径为5.2 cm 的1 号和2 号木,其年龄分别为11年和9年;不同直径的林木,其年龄差异性更加明显,如木荷直径为5.2 cm 的2 号木和直径为7.8 cm 的15 号木,其年龄均为9年。由此可知,利用随机取值的方法对林木初始年龄进行赋值,其年龄的变化规律符合异龄林内林木的生长规律。

表3 木荷的年龄赋值结果Table 3 The age assignment result of Schima superba
3.3 各树种平均年龄的估计
基于样地内木荷、马尾松和杉木的直径与年龄信息,采用Richards 生长方程分别拟合木荷、马尾松和杉木的平均生长过程,其结果见表6。
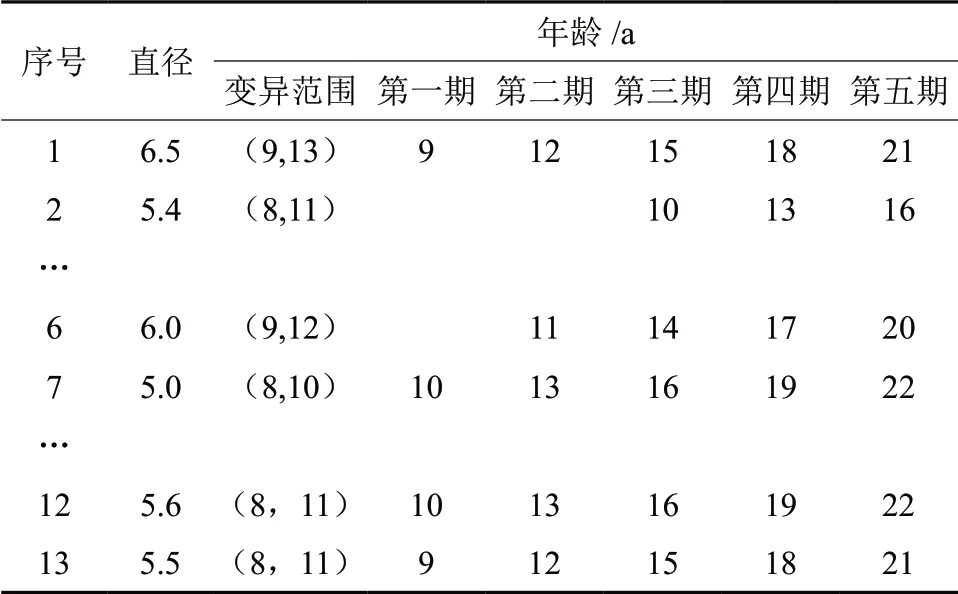
表4 马尾松的年龄赋值结果Table 4 The age assignment result of Pinus massomiana
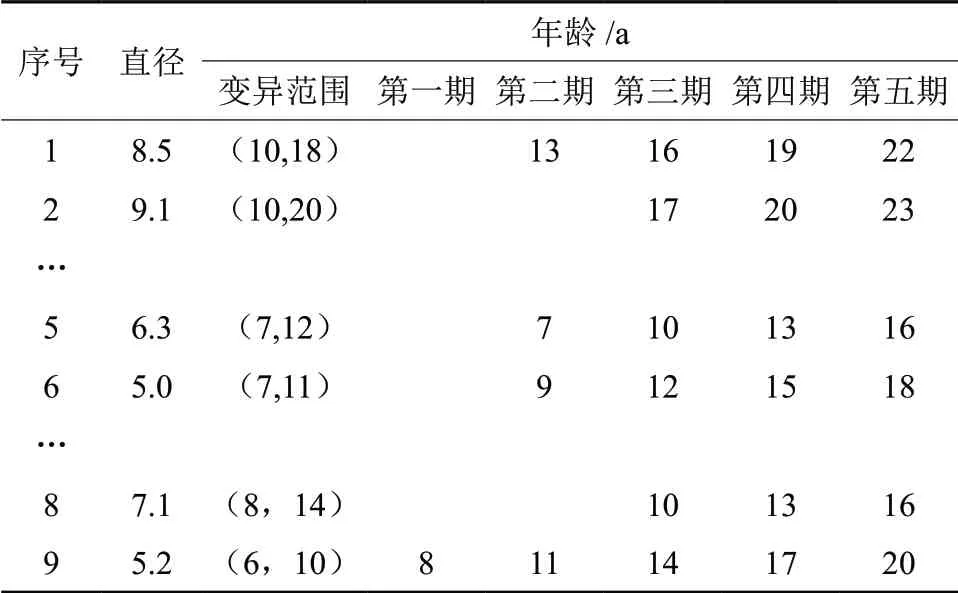
表5 杉木的年龄赋值结果Table 5 The age assignment result of Cunninghamia lanceolata
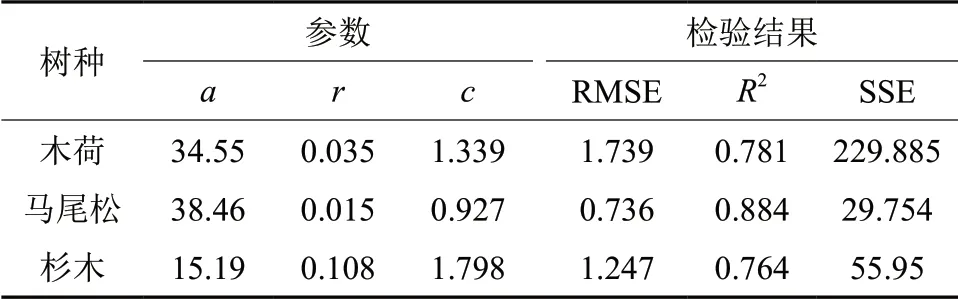
表6 3个树种的生长方程拟合结果Table 6 The fitting results of growth equation of three species
对生长方程求反函数,其表达式为:

式中:A 为林分平均年龄,D 为林分加权平均直径。
利用断面积加权平均的方法计算出2015年木荷林分的断面积加权平均直径D,将D 代入模型(11),计算得出2015年木荷林分平均年龄Ai为22年;同样可计算木荷出林分第一期(2003年)、第二期(2006年)、第三期(2009年)、第四期(2012年)的年龄分别为11 a、14 a、17 a、19 a。为保证年龄估计方法的准确度,利用上述方法对木荷第一期林木初始年龄随机取值10 次,可推算出木荷林分的10 个估计平均年龄。同理,可推算出马尾松和杉木林分的10 个估计平均年龄,对各树种估计年龄与真实年龄进行比较分析,结果如表7。
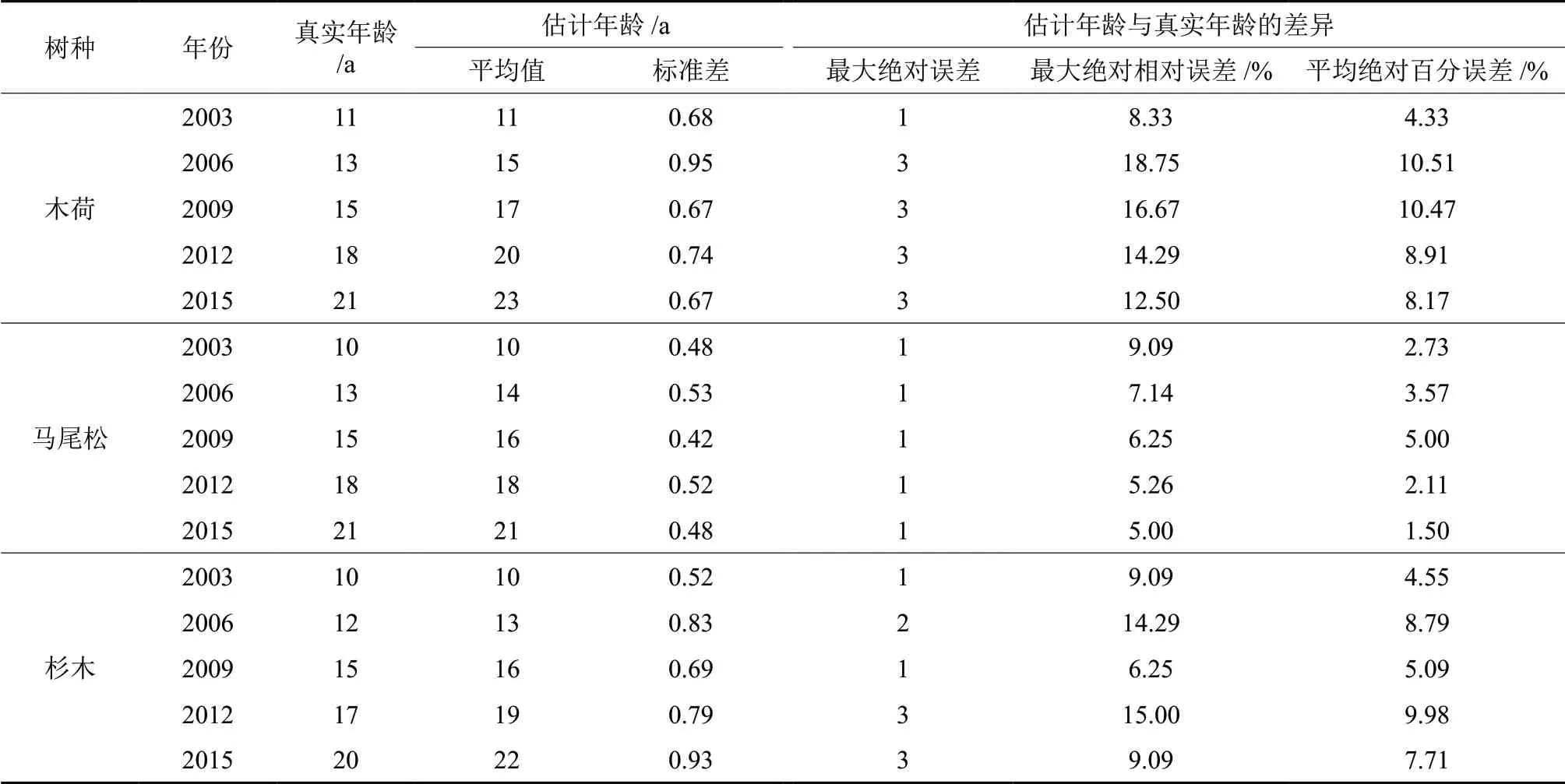
表7 3个树种的估计年龄与真实年龄比较结果Table 7 Comparison of estimated age and true age of three species
由表7可知,估算林分内木荷在各调查期的平均年龄时,木荷10 次估算年龄中与真实年龄的最大绝对误差≤3年,最大绝对相对误差<20%,平均绝对百分误差<11%;估算林分内马尾松在各调查期的平均年龄时,马尾松10 次估算年龄中与真实年龄的最大绝对误差≤1年,最大绝对相对误差<10%,平均绝对百分误差≤5%;估算林分内杉木在各调查期的平均年龄时,杉木10次估算年龄中与真实年龄的最大绝对误差≤3 a,最大绝对相对误差≤15%,平均绝对百分误差<10%。对同一调查期同一树种的年龄进行多次估算时,估算年龄的标准差<1 a,说明该方法估算年龄的效果稳定。
3.4 林分平均年龄的估计
对林分内木荷、马尾松和杉木的直径进行加权平均,估算出林分的平均年龄结果见表8。

表8 林分的估计年龄与真实年龄比较结果Table 8 Comparison of estimated age and true age of stand
由表8可知,该方法估算林分在各调查期的平均年龄时,10 次估计年龄中与真实年龄的最大绝对误差≤3 a,最大绝对相对误差≤15%,平均绝对百分误差<10%,说明利用该方法估算异龄林林分平均年龄的效果较好。
4 结论与讨论
4.1 结 论
研究提出了一种利用林木多期直径测定数据估计异龄林林分年龄的方法,具体步骤为:1)确定林分内各树种的年龄变异范围;2)对林木初始测量直径取随机年龄;3)获取林分内所有林木的直径与年龄信息对;4)利用Richards 方程拟合各树种的直径生长方程;5)代入加权平均直径求算出各树种及林分的平均年龄。
应用年龄估计方法估算异龄林林分及林分内各树种的平均年龄时,估计年龄与真实年龄的最大绝对误差均≤3 a,最大绝对相对误差均<20%,平均绝对百分误差均<11%,说明提出的基于林木多期直径测定数据估计异龄林林分年龄的方法精度较高,适用于林业中异龄林林分平均年龄的估计。
4.2 讨 论
我国的森林资源连续清查[20]是从1973年开始的间隔5年一次的全国森林资源调查工作,连续清查的样地数据特点是持续周期长,样地位置固定,且林木具有多期直径测定数据,但目前研究中对于此类数据的运用不够充分,本研究利用多期直径测定数据来估计异龄林林分的平均年龄,对于了解我国一类清查固定样地的年龄结构具有一定的参考价值。
研究利用5 期直径测定数据来验证年龄估计方法,效果较好,但很多复测数据可能少于5 期,因此利用五期以下的直径复测数据来估计异龄林林分平均年龄时,具体效果如何有待进一步分析。同时,研究选取优势木与被压木来确定林木的年龄变异范围,而现实林分中如果每块样地均选取优势木与被压木进行树干解析,可能成本较高,因此后续研究将进一步分析用统一的年龄变异范围来对林分年龄进行估计的效果。

