曲率组合曲面喷枪轨迹组合优化连接

刘亚举

摘要：针对复杂曲率组合曲面的喷涂机器人喷枪轨迹优化及组合连接问题，基于曲面曲率特性，将其简化为针对大小曲率曲面片上及相交区域喷枪轨迹的优化研究，提出针对复杂曲率组合曲面的喷枪轨迹组合连接算法，实现了对组合曲面的整体快速喷涂，仿真实验验证了该智能算法具有良好的全局搜索能力及快速收敛性，为进一步完善喷涂機器人离线编程系统奠定了基础。

关键词：喷涂机器人;离线编程;喷枪轨迹组合优化;曲率组合曲面

近年来，喷涂机器人以自动化程度高，节能环保等优点被广泛应用于各类喷涂生产中。但随着产品外形设计的复杂化程度不断提升，急需对喷涂机器人离线编程系统建立针对各种复杂待喷涂型面喷枪轨迹优化方法。陈伟等[1]提出将复杂曲面分片后分别进行优化，最后利用改进的蚁群算法将各片轨迹进行优化连接。曾勇等[2]提出了针对大型复杂自由曲面的喷枪轨迹优化方法，但未从曲面曲率角度进行具体化分析。赵德安，[3]张鹏等[4]分别采用遗传算法和粒子群优化算法求解喷枪轨迹组合连接问题，提升了喷涂效率，但未从曲面曲率特性角度研究变曲率组合曲面的喷枪轨迹组合优化连接问题。

综上，需对各种复杂待喷型面建立喷枪轨迹优化方法。本文基于曲面曲率特性将复杂曲面简化为不同曲率曲面的组合，进而优化各个曲率曲面片上及相交区域的喷枪轨迹优化和轨迹组合连接问题，提升喷涂效果。

1涂层累积速率模型的建立

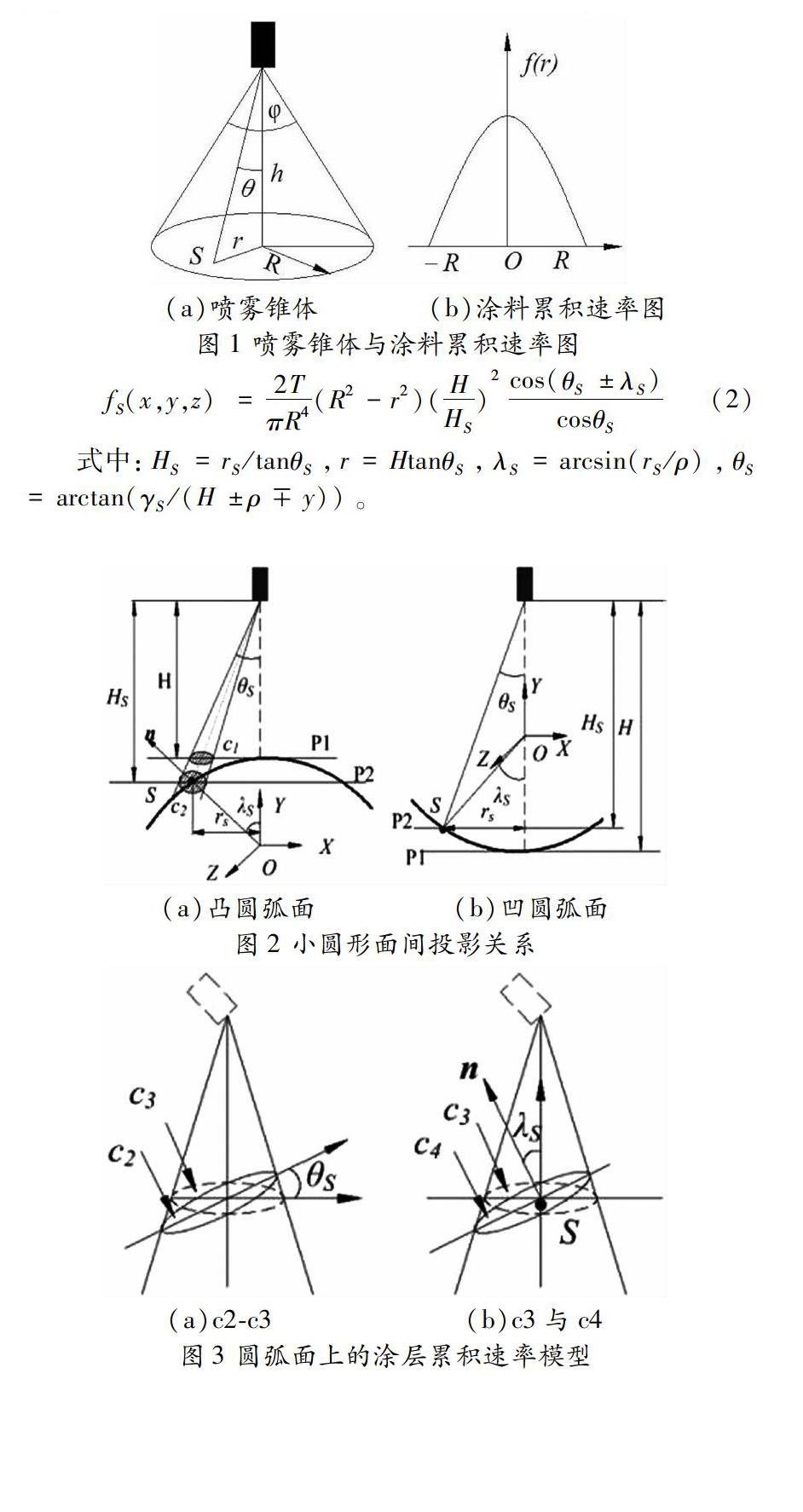
设喷出的涂料雾化形状在三维是圆锥体（如图1a），则其在二维平面生成的分布模型如图1b所示。在喷涂距离保持不变时，设喷涂半径外无涂料累积，则平面上的涂层累积速率模型[5]：f（r）=A（R2-r2），其中R为喷涂半径，r为平面上S点到喷涂中心的距离，A为常数。

实际喷涂生产时，涂料流量一般不变，设涂料流量为T，可求得常数A，上述模型可变为：

因喷涂时喷雾锥不同截面的涂料累积速率不变，可依微分几何学方法[6]建立圆弧面（凸、凹）上的涂料累积情形，如图2。设与圆弧面相切的平面P1为参考面，平面P2与其平行并过S点，θS是喷枪轴线与喷口中心到S点的直线间夹角，H和HS分别是到P1与P2的垂直高度，rS是S点到喷枪轴线距离。设喷射到圆弧面与P1面同等涂料量，且在P1形成的小圆面为c1，c1在P2的投影为c2，小圆形面c3与c2在同一圆锥喷射夹角内且垂直于喷射方向，c4是过S点在圆弧面的小圆形面，λS是c3法向量与c4的法向量n间夹角，如图3。由公式（1）和通过几何运算，可求得考虑涂料流量的圆弧喷枪涂料累积速率新模型：

4曲率组合曲面的喷枪轨迹连接

4.1喷枪轨迹组合分析

完成对曲率组合曲面上单个大小曲率曲面和不同曲率曲面片相交区域的喷枪轨迹优化后，为提高喷涂效率，需找出一条能将各个曲率曲面上的喷枪轨迹连接起来、且只经过各个曲面一次的最短喷枪路径。因此，可将该喷涂问题看成开环乡村邮递员问题，即O-RPP问题。本文基于改进的粒子群算法[9]进行优化求解，算法流程如图6所示。

4.2算法应用

基于算法，选择某复杂曲面，按上文方法将其简化为由小曲率曲面片1，大曲率柱（3、4、5）、锥（2）曲面片组合成的曲率组合曲面，如图7。规划并优化每个曲率曲面片上喷枪轨迹后，需要将所有曲面片上轨迹的起点与终点连接起来，形成一条最短的喷枪路径，使喷枪能沿着该路径喷完所有曲面并且每个曲面仅被喷涂一次。设算法中种群规模为10，最大迭代次数为200，微粒数100，为了应用算法，选择如下十个坐标：[205.5454，380.5827;350.0661，454.9088;363.1773454.9088;497.3883456.9351;502.2936458.9460;576.3848465.3676;573.4007469.3053;478.9153587.6485;470.6608590.2045;389.8969646.2372]。

4.3结果分析

算法运行结果如图8所示，随着进化过程的不断运行，喷枪路径长度呈现快速递减趋势，算法快速收敛，最终趋于稳定不变，在进化到34代得到了976.1902mm的最优路径长度值，说明了此算法在求解文中曲率组合曲面喷枪轨迹组合连接优化问题的时效性，能够极大地提高喷涂效率。

5结语

针对复杂自由曲面，将其具体化为曲率组合曲面进行了喷枪轨迹优化研究，制定了面向复杂曲率组合曲面的喷枪轨迹连接算法，为进一步完善喷涂机器人离线编程系统奠定了基础。

参考文献：

[1]陈伟，赵德安，李发忠.复杂曲面的喷涂机器人喷枪轨迹优化与试验[J].农业机械学报，2011，42（1）：204-208.

[2]曾勇.大型复杂自由曲面的喷涂机器人喷枪轨迹优化研究[D].兰州理工大学，2011.

[3]赵德安，陈伟，汤养.基于遗传算法的喷涂机器人喷枪路径规划[J].中国机械工程，2008，19（7）：777-779+792.

[4]张鹏，龚俊，宁会峰，等.面向大曲率组合曲面的喷涂机器人喷枪轨迹组合与连接问题研究[J].四川大学学报（工程科学版），2016，48（04）：217-222.

[5]GoodmanED，HoppensteradtLTW.Amethodforaccuratesimulationofroboticsprayapplicationusingempiricalparameterization[C].IEEEInternationalConferenceonRoboticsandAutomation，USA：Sacramento，1991：1357-1368.

[6]陈省身，陈维桓.微分几何讲义.北京：北京大学出版社，2001：201-211.

[7]曾勇，龚俊，陆保印.面向复杂曲面的喷涂机器人喷枪路径的规划[J].机械科学与术，2010，29（05）：675-679.

[8]ChenH.P，XiN.AutomatedTooltrajectoryplanningofindustrialrobotsforpaintingcompositesurfaces.AdvManufTechnol，2008（35）：680-696.

[9]任子晖，王坚.动态拓扑结构的多目标粒子群优化算法[J].同济大学学报（自然科学版），2011，39（08）：1222-1226.