叶尔羌河年径流预测模型研究与应用

何兵 高凡 蓝利 覃姗

摘要为提高叶尔羌河中长期径流预测精度，基于小波分析的基础上建立遗传算法优化BP神经网络的耦合模型，对60年叶尔羌河年径流时间序列进行研究。结果表明：耦合模型综合了两者的优势，在保留神经网络优良非线性拟合能力的同时，又融入遗传算法的容错性和全局搜索能力，提高预测径流时的学习速度和泛化能力。在对年径流进行预测时，其预测平均误差为-2.69%，而采用传统单纯的BP神经网络模型预测的平均误差为-10.25%。从预测误差检验以及模型的对比结果可知此模型合理、可行，因此该算法有助于解决叶尔羌河中长期径流预测问题。

关键词径流预测;遗传算法;BP神经网络;叶尔羌河

中图分类号P338文献标识码A

文章编号0517-6611（2019）03-0208-04

doi：10.3969/j.issn.0517-6611.2019.03.065

建立可靠的预测模型历来是水文预测的重要内容，类似的研究成果也较多。受降水、气温及下垫面等多重因素的影响，年径流时间序列具有高度复杂的非线性、非平稳的变化特征，因此很难对其进行预测[1]，尤其针对本底环境极端脆弱的干旱内陆河流地区来说更是一种挑战。如何提高年径流的预测精度，一直是水文工作者的难题，但也成为研究的热点之一。在以往的径流预测研究中，传统的回归模型虽因可操作性强而被广大学者广泛使用，但由于其影响因子的不确定性、不稳定性及因子多重交互性等，难以用简单的线性关系描述，且年径流过程的自相依性较弱，仅应用单一的统计回归模型来预测使得结果难以被认可[2]。随着年径流预测领域的不断发展和完善，径流预测也出现了新的方法，如人工神经网络预测模型[3]、灰色预测模型[4]、支持向量机[5]、遗传算法[6]以及组合模型[3-5]，大致可分为物理成因分析法和数理统计模型2类，但这些统计预测方法各有优缺点，如BP 神经网络模型虽然原理简单易操作，但存在延时、收敛精度不高以及易陷入局部极小点等问题[7]。年径流预测的方法和模型虽然很多，但没有一种统一的方法或模型适用于所有的径流序列[8]。因此，为研究模拟出适用于叶尔羌河流域年径流的预测模型，并与传统的BP神经网络模型做对比，以期提高模拟预测的精度，该研究采用小波分解的信号作为BP神经网络的输入项[9]，其次利用遗传算法能寻优的特点推求出BP神经网络的最优初始权重和阈值，最终建立小波分析—遗传算法优化BP神经网络的耦合模型对叶尔羌河年径流进行研究。目前，国内对叶尔羌河径流特征分析的研究较多，多集中在对径流、降水、气温、蒸发以及生态环境特征等方面[10-13]，而对于年径流的模拟预测研究成果较少。在新疆执行严格的水资源管理制度背景下，对叶尔羌河年径流进行模拟预测，可为流域水资源的合理开发利用、水资源管理等提供理论依据和技术支持，同时也可以为干旱区中小河流的中长期径流预测提供参考。

1研究区概况及数据来源

叶尔羌河是国内最大的内陆河塔里木河的主要源流之一，属冰雪消融补给型河流，发源于喀喇昆仑山脉。叶尔羌河的水量控制站卡群站的集水面积为50 248  km2[14]，多年平均年径流为65.66×108 m3，控制出山口以上河长为527 km，流域面积在国内占9.36×104 km2[15]。叶尔羌河径流由冰川融水、地下水及雨雪水混合补给组成，分别占64.0%、22.6%、13.4%，其年内径流量主要集中在夏季，卡群站6—8月径流量占总径流量的 68.5%[16]。叶尔羌河流域水系由以下河流组成，其中叶尔羌河最大，提孜那甫河次之，柯克亚河与乌鲁克河最小。目前已将提孜那甫河与叶尔羌河通过4条“引叶济提”的水利工程连通;提孜那甫河和柯克亚河、乌鲁克河通过蒙卡提渠也已连通，形成了可统一调度的完整的叶尔羌河水系[17]。

該研究选取卡群水文站共60年（1957—2016年）的资料对径流进行模拟预测。使用前52年（1957—2008年）序列作为模型模拟的训练样本，后8年（2009—2016年）序列作为模型预测的检验样本。

2小波及遗传算法优化BP神经网络模型

BP 神经网络被广泛应用于水文预测预报等领域，不仅因为其结构简单便于理解，而且还具有良好的非线性映射能力[18]。但BP神经网络存在延时、收敛精度不高以及易陷入局部极小点等不可避免的问题，故该研究拟采用小波及遗传算法优化BP神经网络模型。该模型因经小波分解后的每一频率成分都有其自身的约束及发展规律，它既能反映过去随时间的演变，还能预测未来的发展趋势[1]，故将径流序列用小波分解为不同频率的信号，并作为BP神经网络的输入神经元;为提高年径流序列模拟的精度，选用寻优效果良好的遗传算法对BP网络的初始权重和阈值进行优化，并且寻找到最优连接权，从而解决了神经网络收敛速度慢和收敛精度差的问题。

2.2遗传算法优化BP神经网络模型

原序列经过小波分解后能得到不同频率的细节信号，将这些细节信号作为BP网络的输入向量，BP网络的拓扑结构确定后，再确定BP网络的初始权重和阈值时，用寻优能力良好的遗传算法来获得BP网络的最优权值和阈值[21]，继而进行网络测试、误差计算等步骤。如果遗传算法得到的最优解不符合要求，那么再利用 BP 神经网络对初始权重和阈值进行调试直到符合要求为止，以便能够取得满意的模拟结果，其具体优化步骤如下：

式中，n为输入层节点数;m为隐含层节点数;l为输出层节点数。该次试验初始种群的规模为40。

（2）用神经网络误差平方和的倒数来定义适应度函数，计算每个个体适应度值，误差越小，则适应度越大;误差越大，则反之。

（3）产生的最优个体可以直接复制给下一代，其他的个体，使用交叉和变异等操作来进一步的筛选，在该次试验中，交叉概率为0.9，变异概率为0.1，进化代数为30。

（4）重复上述2～3的步骤，直到训练目标的迭代次数达到设定的要求为止。

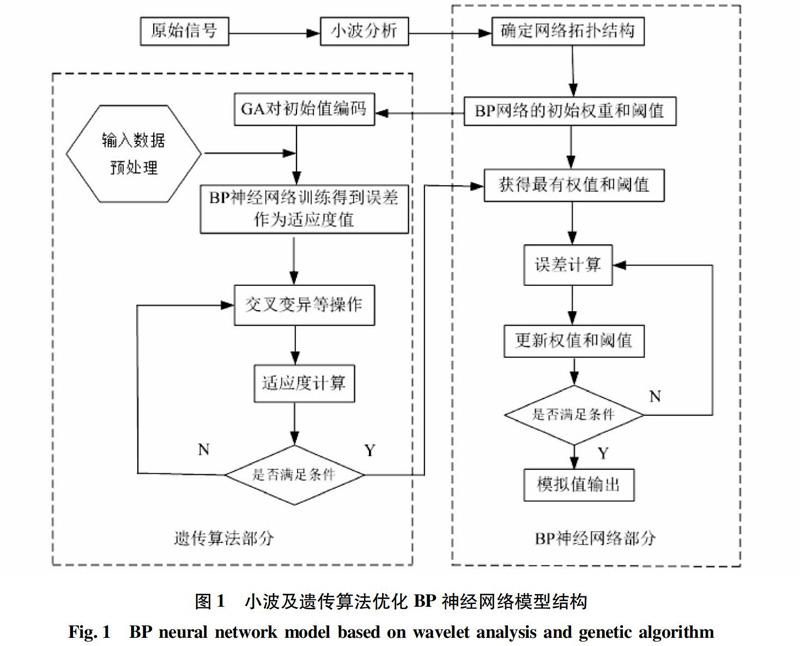
小波及遗传算法优化BP神经网络模型的结构见图1。

3实例分析

3.1模型模拟该研究所做的工作均是在matlab环境下进行。小波分析方面，选用db5小波对叶尔羌河年径流时间序列信号进行小波分解，结果见图2。其中d1到d9是经小波分解后得到的不同频率的信号，可反映年径流序列的细节信息，和原始信号对比后可以看出d1～d5为主信号层，d6～d9为噪声信号层，故可以去掉噪声层，将d1～d5的信号作为BP网络的输入向量，并带入到模型里面进行计算。

将该研究采用的小波及遗传算法优化BP神经网络的模型应用于叶尔羌河年径流时间序列。此模型中，BP 神经网络结构分为输入层、隐含层和输出层，其中，输入层神经元个数为 5，是由小波分解得到的5个主信号层组成;隐含层神经元个数定为11，隐含层节点个数由试算法确定，试算法的思路是取不同的隐含层节点个数分别对样本进行模拟，然后选择模拟效果达到最好时的节点个数，由此确定隐含层个数为11;输出就是最后的模拟值，个数为1。该研究利用1957—2008年的共52年的径流序列样本在优化过的模型中进行训练，并建立模型，利用2009—2016年共8年的实测年径流序列样本进行模拟。遗传算法优化BP神经网络的程序中，种群规模P取30，遗传代数为40，交叉概率Pc取0.9，变异概率Pm取0.1，最后把最优个体作为BP神经网络的初始权值和阈值。采用遗传算法优化BP神经网络，在迭代30次后，适应度值基本趋于稳定（图3）。BP神经网络模型采用的是梯度下降法，误差精度为10-7，学习速率为 0.001。

3.2模型预测

采用适应度值最大的权值和阈值用于网络进行模拟，小波及遗传算法优化BP神经网络模型的预测结果见图4（a）。由图4可知，2009年、2010年这2年模拟的结果与实测年径流值基本接近，2012年、2013年和2016年这3年模拟效果误差稍大，但从整体来看，模拟效果良好。另外，为便于分析比较，同时计算单纯的BP神经网络模型，其结果见图4（b），相比该研究采用的方法，BP神经网络模型除了2010年和实测值接近外，其余年模拟效果都不理想。

表1为两模型模拟值和实测值的具体数值对比，由计算得本文所采用的模型模拟的误差平均值为-2.69%，最大误差值为-8.25%，最小误差值为-1.67%。而BP神经网络模型模拟误差平均值为-10.25%，最大误差值-20.13%，最小-4.92%，也可由图4更为直观的反映此模型模拟效果要比BP神经网络模型模拟好，因此该研究采用的模型可以用来预测未来叶尔羌河年径流时间序列。

根据以上分析和图4（a）可以看出，耦合模型有个别数据模拟精度不高，分析有两点原因：一是因为小波变换采用的实际滤波器与理想滤波器存在的差异性，导致小波分解后的小波系数中存在各种系数混杂现象，相邻的小波系数之间互相受到干扰[23]。这样会导致小波分解后的数据带入到网络模型里存在失真的缺陷。二是年径流时间序列在经过小波分解以及遗传算法寻优的过程中都会产生无法避免的随机误差，以及序列样本的长度限制等，导致模型的部分数据模拟效果欠佳。从整体上看，该研究采用的模型模拟精度要高于单纯的BP神经网络模型，具有一定的参考价值。

4结论与讨论

（1）将小波分析和遗传算法引入到BP神经网络模型中，计算出此模型模拟误差平均值为-2.69%，对比BP神经网络模型模拟误差平均值-10.25%，该模型模拟精度明显高于单纯的BP神经网络模型，故基于小波分解以及遗传算法优化BP神经网络连接权的方法可以提高年径流时间序列模拟的精度，但也有个别数据模拟效果欠佳，大致分析两点原因：一是小波变換特性因素;二是模型误差的影响，表明该模型的方法和精度还有待完善和提高。

（2）目前条件下，依靠以往径流资料来做的径流预测模

型即数理统计模型，由于未考虑其他影响因素，可能会导致

预测精度不理想以及现实意义不大的问题，但在缺乏其他资料地区的情况下，采用此种方法是可行的。该研究以卡群水文站年径流为例进行验证，从预测误差检验以及模型的对比结果可知，在小波分析的基础上建立遗传算法优化BP神经网络的耦合模型是合理且有效的。所建的耦合模型可以用来预测未来叶尔羌河年径流量，也可以为年径流时间序列的预测提供参考。

（3）模型的建立都有一定的适用条件，为找到适合的径流预测模型，单一的方法会受到一定限制，为提高预测精度，将多种方法进行耦合，可以发挥各自优势，扬长避短，从而提高径流预测精度的准确性。

参考文献

[1] 蒋晓辉，刘昌明.基于小波分析的径向基神经网络年径流预测[J].应用科学学报，2004，22（3）：411-414.

[2] 彭欣怡，于国荣，张代青.不同组合小波神经网络模型对径流预测的适用性[J].人民长江，2015，46（24）：24-28.

[3] 李琳琳，岳春芳， 张胜江.基于小波方差分析的BP神经网络年径流预测[J].节水灌溉，2014（6）：44-46.

[4] 晏欣.灰色-人工神经网络组合预测方法在径流中长期预测中的应用研究[D].昆明：昆明理工大学，2013.

[5] 黄巧玲，粟晓玲.基于小波支持向量机耦合的月径流预测方法[J].水力发电学报，2015，34（3）：1-7，20.

[6] 袁晓辉，张勇传，袁艳斌.基于遗传规划的径流预测新方法[J].水力发电，2006，32（8）：11-13.

[7] 郭淳，李祚泳，党嫒.基于免疫进化算法的BP网络模型在径流预测中的应用[J].水资源保护，2009，25（5）：1-4.

[8] 陈汇林，朱凱.年径流的特征及预测研究进展[J].农业与技术，2014，34（1）：162-163，167.

[9] 李祚泳.水文水资源及水环境分析的若干进展[J].四川大学学报（工程科学版），2002，34（2）：1-4.

[10] 杜清，徐海量，张广朋，等.叶尔羌河流域1990—2010年生态环境变化特征[J].干旱地区农业研究，2016，34（1）：252-256，263.

[11] 王修内，黄强，畅建霞.新疆叶尔羌河流域径流规律分析[J].人民黄河，2012，34（6）：45-47，50.

[12] 孙本国，毛炜峄，冯燕茹，等.叶尔羌河流域气温、降水及径流变化特征分析[J].干旱区研究，2006，23（2）：203-209.

[13] 任加国，郑西来，许模，等.新疆叶尔羌河流域土壤盐渍化特征研究[J].土壤，2005，37（6）：635-639.

[14] 古丽孜巴·艾尼，满苏尔·沙比提.叶尔羌河径流量时序变化特征及成因分析[J].科技创新与应用，2014（13）：298-299.

[15] 何兵，高凡，闫正龙，等.叶尔羌河径流演变规律与变异特征[J].水资源与水工程学报，2018，29（1）：38-43，49.

[16] 满苏尔·沙比提， 胡江玲.塔里木河流域水量变化对生态环境影响分析[J].干旱区资源与环境，2007，21（10）：83-87.

[17] 朱芳芳.浅议叶尔羌河水文特征[J].中国水运，2015，15（3）：182-183.

[18] 崔东文.多隐层BP神经网络模型在径流预测中的应用[J].水文，2013，33（1）：68-73.

[19] 刘素一，权先璋，张勇传.小波变换结合BP神经网络进行径流预测[J].人民长江，2003，34（7）：38-39.

[20] 李淼，夏军，陈社明，等.北京地区近300年降水变化的小波分析[J].自然资源学报， 2011，26（6）：1001-1011.

[21] 仲云飞， 梅一韬， 吴邦彬，等.遗传算法优化BP神经网络在大坝扬压力预测中的应用[J].水电能源科学，2012，30（6）：98-101.

[22] 肖迁，李文华，李志刚，等.基于改进的小波-BP神经网络的风速和风电功率预测[J].电力系统保护与控制，2014（15）：80-86.

[23] 何岭松.小波函数性质极其对小波分析结果的影响[J].振动工程学报，2000，13（1）：143-145.