基于SOM神经网络的二阶变异体约简方法∗

宋 利,刘 靖

(内蒙古大学 计算机学院,内蒙古 呼和浩特 010021)

变异测试[1]是一种通过向源程序中人工注入缺陷来模拟软件中实际缺陷的技术,被注入缺陷的程序称为变异体.传统的变异测试是指一阶变异测试,即通过向源程序中人工注入一个缺陷来模拟软件中的一个缺陷[2].但程序中的实际缺陷往往是由两个或者更多个缺陷一起造成的[3,4],所以高阶变异测试被提出来用以解决程序中复杂缺陷的问题,在模拟程序的复杂缺陷方面有着重要意义[5].

由一阶变异体组合形成的高阶变异体数量会大量增加,大大增加了执行开销[6,7].因此,减少高阶变异体数量和发现隐藏高阶变异体(subtle higher-order mutant)已经成为当前高阶变异测试的研究热点[8].

启发式算法被应用于高阶变异测试中解决高阶变异体数量[9-11]的问题,有效减少了高阶变异体的数量,降低了程序的执行开销,但却会存在未被发现错误组合的缺点,这将降低测试组件质量.启发式算法也被应用于解决发现隐藏高阶变异体的问题[12,13],虽克服了未被发现错误组合的缺点,但却增加了时间开销.与此同时,聚类法被证明在变异体约简上有很好的效果[14,15].Ma等人[14]使用聚类法在不影响变异充分度的前提下减少了变异体数量,降低了程序的执行开销,但在运用到高阶变异测试时却因缺乏传值而受限.针对该问题,本文着重研究二阶变异测试.本文分析了影响二阶变异体执行过程中中间值相似性的因素,并将该中间值相似性描述为条件下二阶等价变异体,使用基于SOM神经网络模型[16,17]的方法进行变异体聚类以达到充分考虑二阶变异体组合时减少二阶变异体执行开销和发现隐藏二阶变异体(subtle second-order mutant,本文定义为二阶变异体中单独的一阶变异体均被测试例杀死,但两者结合后的二阶变异体不能被现有测试例杀死的二阶变异体)的效果.

本文第1节介绍相关工作.第2节是本文方法中用到的基础概念.第3节对所提方法进行具体的介绍.第4节对所提方法进行理论分析.第5节给出实验结果及分析.第6节是本文的结论.

1 相关工作

在变异测试中,如果在同一测试例下,变异体的结果和原始程序的结果不同,则称该变异体被杀死,否则它是存活的.被杀死的变异体个数与所有的非等价变异体个数的比值称为变异充分度[2].传统的变异体是指通过在原始程序中注入一个缺陷而产生的一阶变异体.实际上,Purushothaman和Perry已经证明,程序中存在的许多缺陷都是复杂的,这类缺陷无法使用一阶变异体进行模拟.为了解决该问题,高阶变异体则通过在原始程序中注入两个或更多个故障来模拟程序中的复杂缺陷.然而高阶变异测试的成本却很高,因此,降低高阶变异测试的成本是非常重要的.

关于降低高阶变异测试成本方法的研究已经有很多学者在探索,综述文献[8]对相关研究进行了很好的总结分析.其中,减少高阶变异体数量的方法主要有3种不同类型:第1种是选择有价值的高阶变异体,如基于搜索的软件工程的遗传算法[5];第2种是减少变异算子的数量,例如last-to first的变异算子选择算法和互不同的变异算子选择算法[9,10];第3种是减少变异位置的个数,如数据流技术[11,18].关于发现隐藏高阶变异体的方法[8]则更多的关注于使用基于搜索的软件工程中的贪婪和遗传算法的方法来解决[6,12,13].

与此同时,聚类法已经在变异测试中得到了很好的应用[14].该方法综合考虑了动态变异体和变异体筛选的优点.研究表明,该方法在减少变异体数量方面具有很好的效果.虽然聚类法已经在变异测试领域取得了很大进展[14,15,19,20],但是该方法更注重减少一阶变异体的数量并且缺乏中间结果的保存.因此,我们在二阶变异测试中尝试采用一种新的方法,即应用SOM(self-organizing map)神经网络方法进行聚类.

SOM 神经网络[16]是通过模拟大脑神经系统自组织特征映射功能进行的一种无监督竞争式学习前馈网络,经过神经网络学习提取数据中的重要特征或某种内在规律,对数据进行聚类.而SOM神经网络的学习算法则是通过模拟生物神经元之间的兴奋、协调与抑制、竞争作用的信息处理的动力学原理来指导网络的学习与工作.所以该网络具有很强的聚类能力,并且在各领域得到了广泛的应用[17].

本文分析了影响二阶变异体执行中间值相似性的因素.基于因素分析,提出了一种使用SOM神经网络聚类模型进行变异体约简及发现隐藏二阶变异体的方法.具体而言,首先对不同变异点处的变异体组合成二阶变异体,在此基础上进行基于 SOM 神经网络聚类模型的变异体约简,根据不同变异点组合中间结果是否一样为一类,然后从每一簇中选择一组变异体进行继续执行,达到对二阶变异体进行聚类和发现隐藏二阶变异体的效果.

2 条件下二阶等价变异体

二阶变异体的约简原理,主要是根据二阶变异体执行过程中的中间值相似性,即条件下二阶等价变异体进行的,所以本节就条件下二阶等价变异体的概念给出相关定义和示例.

2.1 概念定义

a)等价变异体:指对于任何测试数据,执行源程序和变异体后,输出结果相同的变异体[20];

b)变异体被杀死:指对于相同的测试数据,分行执行变异体和源程序,若变异体和源程序的执行结果不同,则称该变异体被杀死[20];

c)条件下等价变异体(conditionally overlapped mutants):指对于相同的测试用例,一组一阶变异体的中间结果相同,但是有可能会被该测试用例杀死的一组变异体[14];

d)二阶变异体的中间结果:本文定义为仅运行至二阶变异体中两个变异点后得到的结果,而非运行完整个程序后得到的结果,记为intermediate results of second-order mutants,简单记为Irs;

e)条件下二阶等价变异体:本文定义为对于相同的测试用例,一组二阶变异体的中间结果相同,但可能会被该测试用例杀死的一组二阶变异体,记为second-order conditionally overlapped mutants,简单记为Second_CoM.

2.2 条件下二阶等价变异体示例

为易于理解本文所提出的”条件下二阶等价变异体”概念,以图1(a)所示 Java片段为例进行说明.先使用关系运算符ROR和算术运算符AOR分别作用于程序中的第3行、第7行,生成各自的一个一阶变异体如图1(b)、图1(c)所示;再同时作用于第3行和第7行生成一个二阶变异体如图1(d)所示.

Fig.1 A Java example for related concepts图1 相关概念的Java示例

以(A=4,B=2)作为测试数据分别执行源程序和二阶变异体,得到的测试数据信息见表1所列.

由表1可知,一共生成了28个二阶变异体,其中最后一列分别为28个二阶变异体的中间结果.根据条件下二阶等价变异体Second_CoM的概念可知,运行全部程序只需6个二阶变异体即可.理由如下:由变异算子组合ID为1,5,17,21的二阶变异体的中间结果为-8;变异算子组合ID为2,6,18,22的二阶变异体的中间结果为-6;变异算子组合ID为3,7,19,23的二阶变异体的中间结果为-2;变异算子组合ID为4,8,12,16,20,24,28的二阶变异体的中间结果为0;变异算子组合ID为9,13,25的二阶变异体的中间结果为8;变异算子组合ID为10,11,14,15,26,27的二阶变异体的中间结果为2.即该测试例下,共有6组条件下二阶等价变异体,每组条件下二阶等价变异体具有相同的被杀死可能性.所以只需从每一组中选择一个二阶变异体继续运行即可,因此,运行整个程序只需6个二阶变异体.

从示例可以看出,对于条件下二阶等价变异体,因为条件下二阶等价变异体中的二阶变异体中间结果的相似性,所以继续执行程序至最终结果时也一样.因此只需从每一簇中选择一个二阶变异体继续运行即可,这与执行全部的二阶变异体相比会节省很多时间.所以本文提出使用SOM神经网络对条件下二阶等价变异体进行聚类,以减少执行二阶变异体的时间.

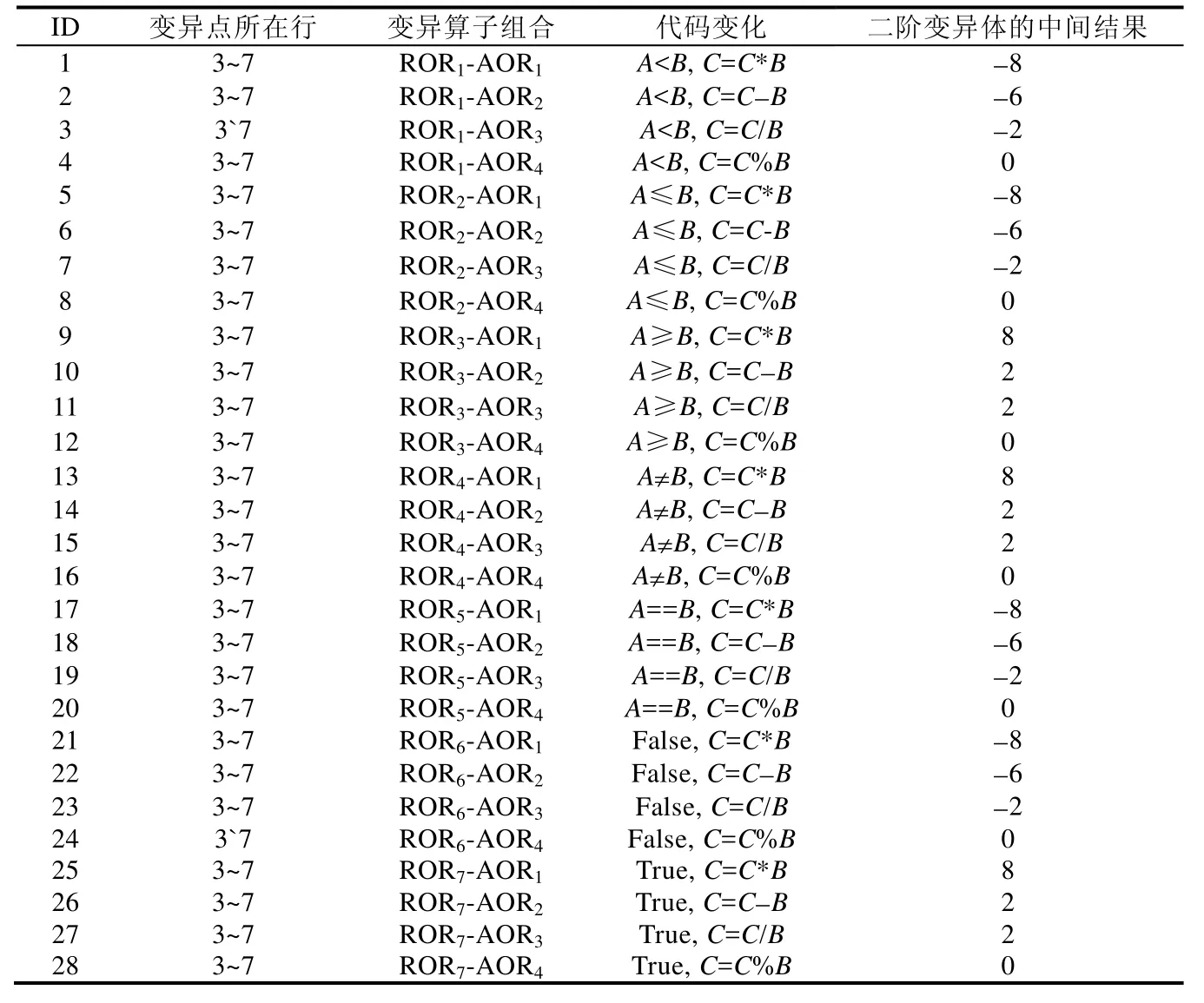
Table 1 Intermediate results of second-order mutants for the example表1 示例中二阶变异体的中间结果

3 基于SOM神经网络的二阶变异体约简方法

基于SOM神经网络的二阶变异体约简方法的总体框架如图2所示.

Fig.2 Framework of second-order mutant reduction based on SOM neural network图2 基于SOM神经网络的二阶变异体约简的框架

该方法主要包括3个步骤,本节接下来将详细阐述这3个步骤.

3.1 二阶变异体的产生

如图2所示,本文中二阶变异体的生成部分主要由以下3步组成.

(1) 一阶变异体生成:使用变异测试工具muJava进行一阶变异体的产生.

(2) 组合策略:提出使用更为全面的缺陷组合策略对一阶变异体组合形成二阶变异体.即对任意两个不同位置处的任意两个一阶变异体进行组合,以充分模拟程序中的复杂缺陷.以第 2.2节例子进行说明,第3行的7个变异体与第7行的4个变异体进行充分组合,产生28个二阶变异体,能够将这两个变异点处的全部错误组合表示出来.

(3) 二阶变异体生成:首先对两个一阶变异体逐行读取,然后根据一阶变异体中变异点行数和变异算子组合等信息替换掉对应的语句形成二阶变异体.为了二阶变异体在执行测试示例时能够及时获取二阶变异体中间结果,本文对muJava工具的源码进行了修改,算法1描述了以变异算子AOR为例的修改.

算法1.含中间结果输出的变异体生成.

输入:源程序语句,原始表达式,AOR算子作用于变异点以后的表达式.

输出:含中间结果显示的变异体的.java文件.

以上即为二阶变异体的生成过程,接下来将分析影响条件下二阶等价变异体的因素,从而确定SOM神经网络中的特征属性.

3.2 特征属性的分析和确定

本文在运用SOM神经网络对二阶变异体进行聚类时,首先分析了影响条件下二阶等价变异体的可能性因素,并将其作为输入层特征属性.主要从以下3个方面进行分析.

(1) 影响二阶变异体被杀死的原因

当二阶变异体的中间结果与源程序不同时,二阶变异体也会被杀死,所以本文根据二阶变异体的中间结果进行分析,以确定二阶变异体被杀死的原因.二阶变异体中按照两个变异点的先后顺序,分别记为第 1变异点和第2变异点.图3所示为根据两个变异点组合的变异体的执行结果进行的分类分析.

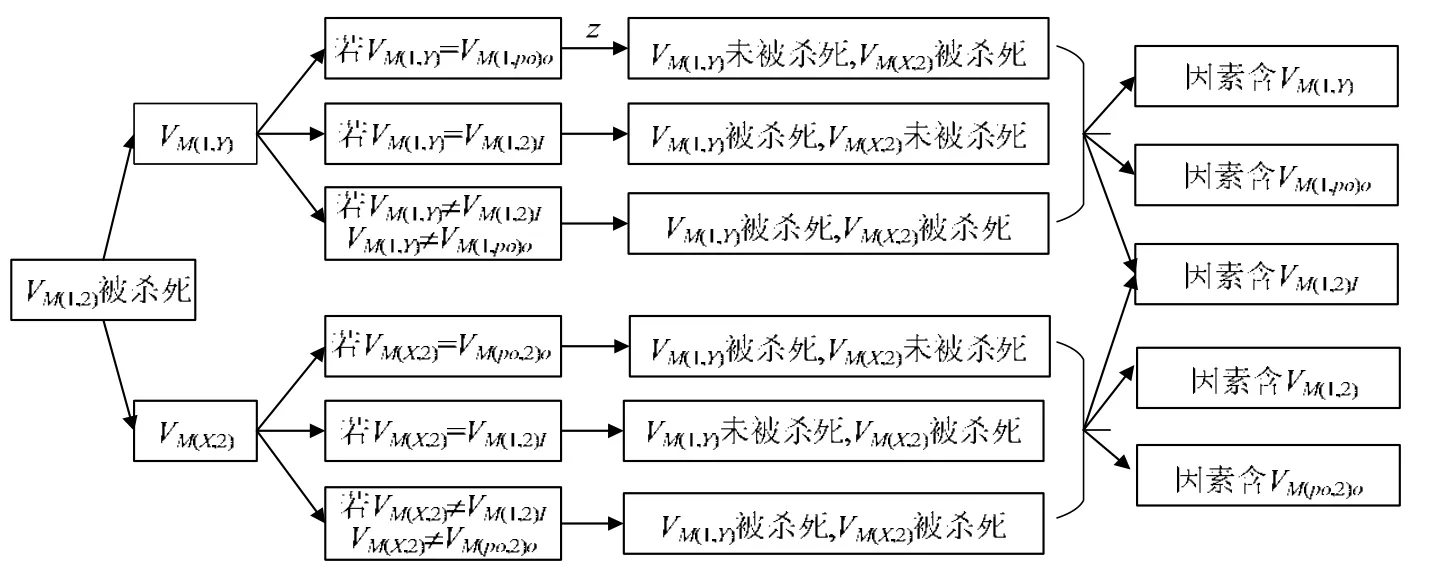
Fig.3 Analysis of the causes of second-order mutants being killed图3 二阶变异体被杀死的原因分析

具体分析如下.

当某二阶变异体被杀死时,可能的原因是二阶组合中的两个一阶单独或者共同造成二阶变异体被杀死的,现分为两种情况进行分析讨论.

a.假设第1变异点变异后的结果(记VM(1,Y)为)造成二阶变异体被杀死,则又可分如下3种情况分析.

· 若VM(1,Y)与第 1变异点的预期结果(两者不发生变异时,由第1个变异点运行至第2变异点时的结果,记为VM(1,po)o)相同,则该假设“VM(1,Y)造成二阶变异体被杀死”不成立.又因二阶变异体被杀死,所以在VM(1,Y)=VM(1,po)o条件下,造成二阶变异体被杀死的原因是第2变异点变异后的结果(记为VM(X,2))造成的.即VM(1,Y)未被杀死,VM(X,2)被杀死时导致了二阶变异体被杀死.

· 若VM(1,Y)与二阶变异体的中间值(两个变异点同时变异时,运行至第 2变异点时的结果,记为VM(1,2)I)相同,所以VM(1,Y)与源程序结果不同,导致VM(1,Y)=VM(1,2)I.又因VM(1,2)I的结果与源程序不同,所以VM(1,Y)造成了二阶变异体被杀死.即VM(1,Y)被杀死,VM(X,2)未被杀死时导致了二阶变异体被杀死.

· 若VM(1,Y)≠VM(1,po)o,VM(1,Y)≠VM(1,2)I说明VM(1,Y)与源程序的第 1变异点的预期结果不同,所以导致VM(1,Y)≠VM(1,po)o;但是VM(1,Y)≠VM(1,2)I,说明VM(X,2)在VM(1,Y)上再次改变了二阶变异体的中间值,导致VM(1,Y)≠VM(1,2)I.即VM(1,Y)被杀死,VM(X,2)被杀死时导致了二阶变异体被杀死.即VM(1,Y)被杀死,VM(X,2)被杀死时导致了二阶变异体被杀死.

b.假设第2变异点变异后的结果(VM(X,2))时造成的,则又可分如下3种情况分析.

· 若VM(X,2)与第2变异点的预期结果(两者不发生变异时,运行至第2变异点时的结果,记为VM(po,2)o)相同,则该假设“VM(X,2)造成二阶变异体被杀死”不成立.又因为二阶变异体被杀死,所以在VM(X,2)=VM(po,2)o条件下,造成二阶变异体被杀死的原因是VM(1,Y)造成的.即VM(1,Y)被杀死,VM(X,2)未被杀死时导致了二阶变异体被杀死.

· 若VM(X,2)=VM(1,2)I,所以VM(X,2)与源程序结果不同,导致VM(X,2)=VM(1,2)I.又因VM(1,2)I的结果与源程序不同,所以VM(X,2)造成二阶变异体被杀死.即VM(1,Y)未被杀死,VM(X,2)被杀死时导致了二阶变异体被杀死.

· 若VM(X,2)≠VM(po,2)o,VM(X,2)≠VM(1,2)I,说明VM(X,2)与源程序的第 2变异点的预期结果不同,故导致VM(X,2)≠VM(po,2)o;但VM(X,2)≠VM(1,2)I,说明VM(1,Y)在VM(X,2)上再次改变了二阶变异体的中间值,导致VM(X,2)≠VM(1,2)I.即VM(1,Y)被杀死,VM(X,2)被杀死时导致了二阶变异体被杀死.

分析了二阶变异体的中间结果被杀死的原因后,可知影响二阶变异体的中间结果相似性,即影响条件下二阶等价变异体的因素含

(2) 分析直观的影响因素

众所周知:当二阶变异体被杀死时,与两个变异体在程序中的位置以及变异算子等有关.现在以经典的三角形程序中的部分代码为例进行说明,如图4所示.

Fig.4 Analysis of intuitive factors图4 直观影响因素的分析

对程序的第1行、第5行语句分别施加ROR变异算子和AOR变异算子,可以得到:如果第1变异体为真时,则第2变异体的结果对程序的最终结果无影响;当第1行语句为真时,则第3行～第16行任意变异点的结果均对最终结果无影响.所以,影响二阶变异体中间结果的因素含测试用例、变异点位置、变异算子、两个变异体的距离.

(3) 影响隐藏二阶变异体的因素

根据隐藏二阶变异体的定义,即二阶变异体中单独的第 1变异体和第 2变异体均被杀死,但两者组合后的二阶变异体没有被杀死的二阶变异体.因此,因素中必含两个变异点分别变异前运行至对应变异点时的预期结果(记为VP(1,po)o和VP(po,2)o)、两个变异点分别变化后运行至对应变异点时的结果(记为VM(1,po)I和VM(po,2)I)、两个变异点同时发生变异后的结果(即VM(1,2)I).注意,VM(1,po)o和VP(1,po)o的区别是:VM(1,po)o表示只有第1个变异点发生变异、第2个变异点未发生变异时的预期结果;VP(1,po)o表示源程序中任意两个变异点均未发生变异时,第1个变异点的预期结果.同理,VM(po,2)o和VP(po,2)o的区别也是如此.

综上所述,本文使用SOM神经网络聚类时的特征属性为:测试用例、变异点位置、变异算子、两个变异体的距离、.

3.3 SOM神经网络的设计

通过第2.2节的分析,确定了影响二阶变异体中间结果的因素.接下来建立适用于二阶变异体的SOM神经网络.

（2）铸造缺陷的修复 铸造厂家对发现的铸造缺陷进行补焊，由于补焊时未预热，焊后未及时进行正火，导致补焊处在中频感应淬火时出现淬火裂纹。由于铸造毛坯经补焊后进行粗加工，导致补焊位置不易识别，在淬火过程中由于应力作用而出现裂纹问题，因而铸造厂家调整补焊工艺，增加焊前预热和焊后正火，以细化晶粒。

根据第2.1节中的方法获取到一阶变异体和二阶变异体的中间结果的信息,将这些信息作为输入层初始数据.对其中的非数值信息,进行ASCII编码转换.本文中的SOM神经网络是在PyCharm中实现,算法的主要步骤和实现如图5所示.

Fig.5 Implementation of SOM neural network algorithm图5 SOM神经网络算法的实现

其核心学习算法每一步的具体实现如下.

(1) 初始化

令获取到的信息为输入数据集dataSet,从训练集中随机取一输入模式并进行归一化处理;竞争层中,各神经元对应的內星权向量为com_weightj(j=1,2,...,m),m为输出层神经元数目,对其进行归一化处理.归一化的方式如公式(1)和公式(2),建立初始优胜邻域和学习率初值设为0.9.

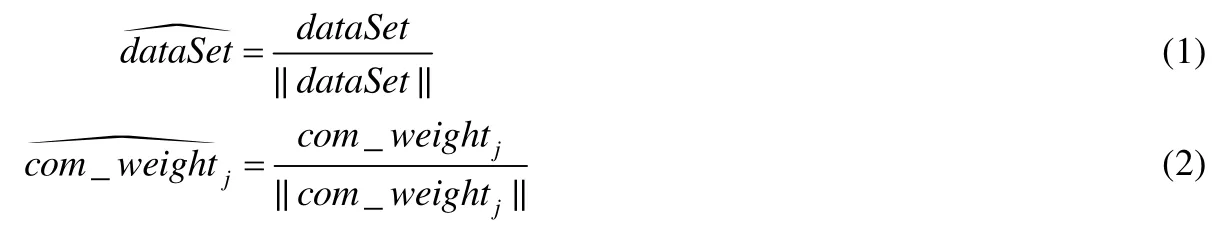
(2) 寻找获胜神经元

根据影响二阶变异体的中间结果的因素,本文中,获胜神经元的计算方式为计算输入样本与权值向量的欧几里得距离(记为dj).即计算输入数据集dataSet归一化后的数据与竞争层中所有神经元对应的內星权向量com_weightj(j=1,2,...,m)的欧几里得距离,如公式(3):

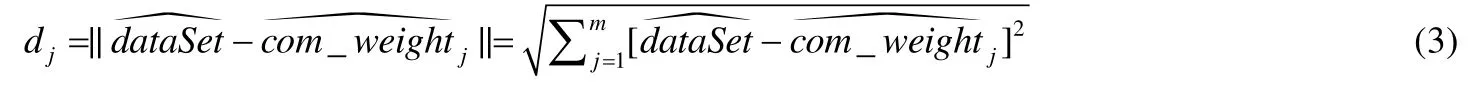
距离最小的神经元赢得竞争,即距离越小的神经元相似度越大,更容易聚为一类.

(4) 调整权值

(5) 重新归一化处理

权向量经过调整后,得到的新向量不再是单位向量,因此要对学习调整后的向量进行重新归一化,循环运算,当eta(t,N)≤etamin时结束训练.不满足时重新进行步骤(1),直到学习率为0.

最后,使用聚类后的约简过的二阶变异体进行程序的完整执行,即强变异测试.

以上 3小节即为本文所提方法的 3个步骤,能充分模拟程序中的复杂缺陷,并且减少程序执行开销的预期效果.接下来,从理论上进行分析和证明所提方法的正确性和有效性.

4 理论分析

为了更加清晰和唯一确定地理解所提出的方法,该节采用Shin等人[21]提出的变异测试的数学理论框架,对本文所提方法的核心理论进行分析和证明.该框架是以程序与程序的差异性为基础展开的,而非程序的正确性.即该框架具有能够说明两个变异体是否能够产生相同结果的功能,而非仅限于说明某个(些)变异体的结果与源程序之间是否相同.同时,所提方法也是基于二阶变异体的中间结果的比较进行的,所以可以使用该框架进行理论分析和证明.本节将从两方面进行数学分析和证明,即变异体约简和发现隐藏二阶变异体.

4.1 变异体约简理论分析

为方便分析和证明,从基于SOM神经网络的聚类结果中的每簇中任选一个二阶变异体用以构成最小二阶变异体集时,以选取每簇中的第1个二阶变异体为例进行分析(实际上,从每簇二阶变异体中选取的需要完全执行的二阶变异体是随机的).给定全部的二阶变异体和测试用例集.假设产生的全部二阶变异体一共有Mall个,聚类后有N个簇,分别编号为M1,M2,...,MN,也就是S_Coms={M1,M2,...,MN};假设簇M1中现有变异体m个,分别简单编号为M1x1,M1x2,...,M1xm;假设N个簇中的任意簇中的二阶变异体的个数为y,例如选取M1中的二阶变异体的个数为y.现选取簇M1中的任意一个变异体作为原点,例如以M1x1作为原点,则簇M1中的所有变异体的中间结果之间相似性可以用数学表示为

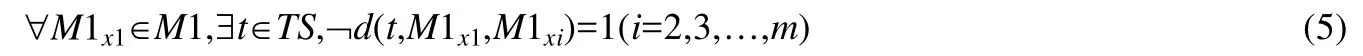
其中,d表示测试差分(简称差分).测试差分表示了程序之间的差异性[21],可用公式(6)[21]表示.

在理论框架中,原点对于公式所表示的内容具有重要意义,而公式(5)中选取M1x1作为原点,则表示M1xi与M1x1的差异性.

公式(6)显示了在相同测试用例下,如果两个程序的运行结果不同,差分d记为1;否则记为0.类似的,采用该框架表示本文中变异体之间的差异性时,可用如下公式表示.

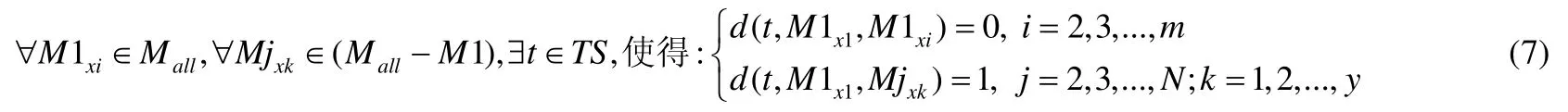
其中,Mjxk表示某一簇中的任意一个二阶变异体.该公式显示了同一簇中的二阶变异体具有相同的二阶变异体的中间结果(即Irs).由于同一簇中的二阶变异体具有相同的Irs,因此测试差分的值为0.不同簇中的二阶变异体具有不同的Irs,所以测试差分d的值为1.

结合公式(5)和公式(7),本文中的二阶变异体的约简原理可作如下推导.

其中,公式(8)中,Mall为全部二阶变异体;公式(9)中,Mi是第i簇二阶变异体;公式(10)中,Mix1表示第i簇中的一个二阶变异体.结合本文选取和确定的特征属性决定了每簇中的二阶变异体具有相似的功能,若该集合具有某种功能,则该集合中的任意一个二阶变异体均具有相似的功能.每簇中选取的二阶变异体构成的新的集合具有全部二阶变异体的功能.

综上所述,理论上,采用本文方法聚类后的二阶变异体个数会减少很多,且不影响原来二阶变异体的测试总结果(例如错误组合的表示情况).

4.2 隐藏二阶变异体理论分析

所提方法发现隐藏二阶变异体的方法和执行步骤为:使用SOM神经网络聚类后,找到某一测试例下的隐藏二阶变异体;找出所有测试例下的隐藏二阶变异体,提取出不同测试例下相同的隐藏二阶变异体,即为找到的隐藏二阶变异体.这些隐藏二阶变异体不能被现有的测试用例杀死.其中,对于某一测试用例下隐藏二阶变异体的数学模型为

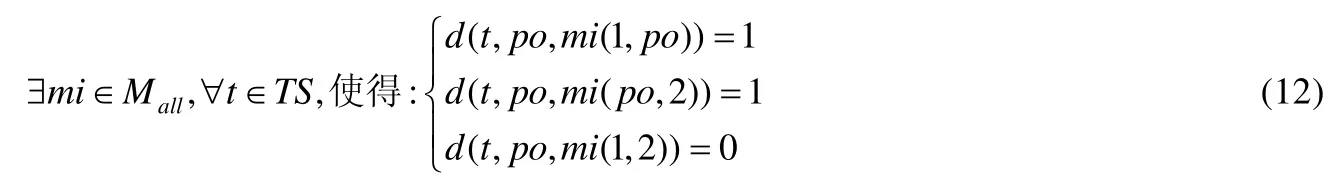
其中,po为源程序;mi(1,po)表示第1个变异点处变异体结果被杀死,第2个变异点未发生变异的变异体.由公式(6)可知,测试差分的值表示该簇中任意一个二阶变异体与测试用例的运行结果情况,所以公式(12)可用于表示某测试例下的隐藏二阶变异体.

但是,使用本文方法时需要找出所有测试例下的隐藏二阶变异体,即需找到满足公式(13)的二阶变异体.

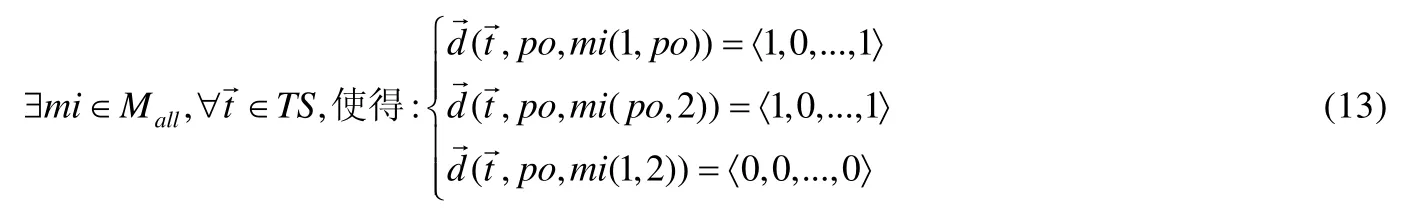
其中,此处的测试用例和差分均使用了矢量,指多个测试用例下的隐藏二阶变异体[21].差分矢量结果中若有混合的1和0,则它们的顺序是任意的(因为变异体可能是被任意测试用例杀死,而不局限于被第1个和最后一个测试用例杀死),此处均记为〈1,0,...,1〉;若只有 0,则没有测试用例可以杀死该变异体.针对多个测试用例下找到隐藏二阶变异体的过程可使用程序空间[21]进行分析,对程序空间改进后,发现隐藏二阶变异体的过程如图6.其中,深黑色圆圈指变异体被测试用例杀死,浅灰色圆圈指未被杀死.图6(1)～图6(3)表示了某二阶变异体在只有一个变异点被杀死时,该二阶变异体能够被3个测试例t1～t3中任意一个测试例杀死;但是如果两个变异点均发生变异后,该二阶变异体反而不能被 3个测试用例杀死,即图6(4)所示.此时需添加新的测试用例来杀死该隐藏二阶变异体,即如图6(5)所示;图6(6)表示推广到二阶变异体中有多个隐藏二阶变异体,然后针对不同隐藏二阶变异体设计新的测试用例(如图6(7)所示),使得该隐藏二阶变异体被杀死,用以提高测试组件的质量.

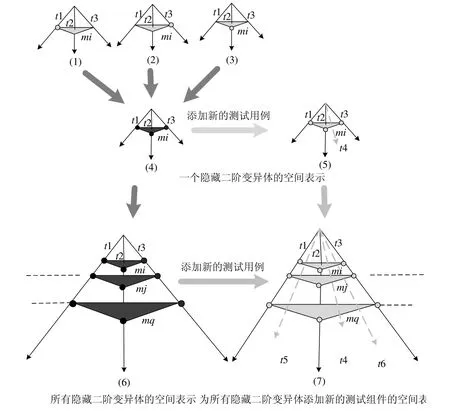
Fig.6 Mathematical model of finding subtle second-order mutants图6 发现隐藏二阶变异体的数学模型

针对多个测试用例下的多个隐藏二阶变异体添加新的测试例前后的变化,使用差分矢量可表示为

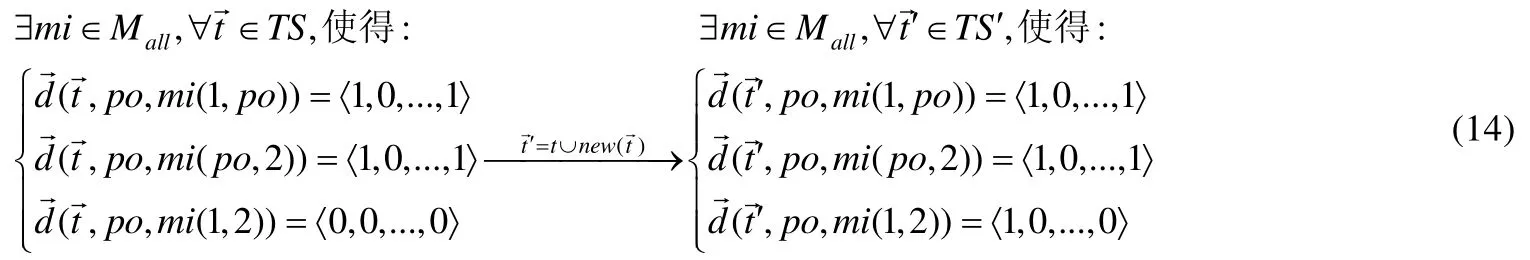
通过使用数学理论框架对本文所提方法进行的分析和理论证明,使得本文所提方法的核心思想更加地容易理解.更重要的是,使用框架中的元素对本文中的方法进行了推导证明,证明了方法的正确性和有效性.接下来,将从实验上验证所提方法的实际效果.

5 实验及结果分析

5.1 实验准备

(1) 程序和实验环境

本文首先选取两个经典的基准程序,即三角形(Triangle)[7,11,14]和找中间数(Mid)[7,11,14]来进行验证,然后使用规模较大的实用性开源项目 Snake和小组团队开发程序 Shopping来验证方法的可应用性和有效性.实验运行环境为Eclipse集成开发环境,实验中的一阶变异体由修改后的muJava工具产生,聚类后变异体由SOM神经网络聚类后产生,基准程序中的测试用例来源于文献[11],实用性项目因为现有文献中没有相同的项目资料,所以使用自己团队编写的测试用例用来验证.因每次对同一数据聚类的结果有细微偏差,所以本文选择其平均值.

(2) 变异算子

本文选取研究中经常使用的变异算子[7,11,14]来进行实验.在符合优秀程序员准则后的程序中,算术运算符、关系运算符和条件运算符等出错的概率比较高,所以这 7个变异算子覆盖了多数程序语言中缺陷常出现的情况,所以这些变异算子具有一定的代表性.其信息见表2.

Table 2 List of mutation operators表2 变异算子列表

其中,

· AOIS表示算术运算符插入,包含有两个操作符,分别为“++,--”.变异点的变异例如“a⇒a--”;

· AOIU表示一元算术运算符插入,包含一个操作符,即“-”.变异点的变异例如“a⇒-a”;

· LOI表示逻辑运算符插入,包含一个操作符,即“～”.变异点的变异如“if (b==a)⇒if (b==～a)”;

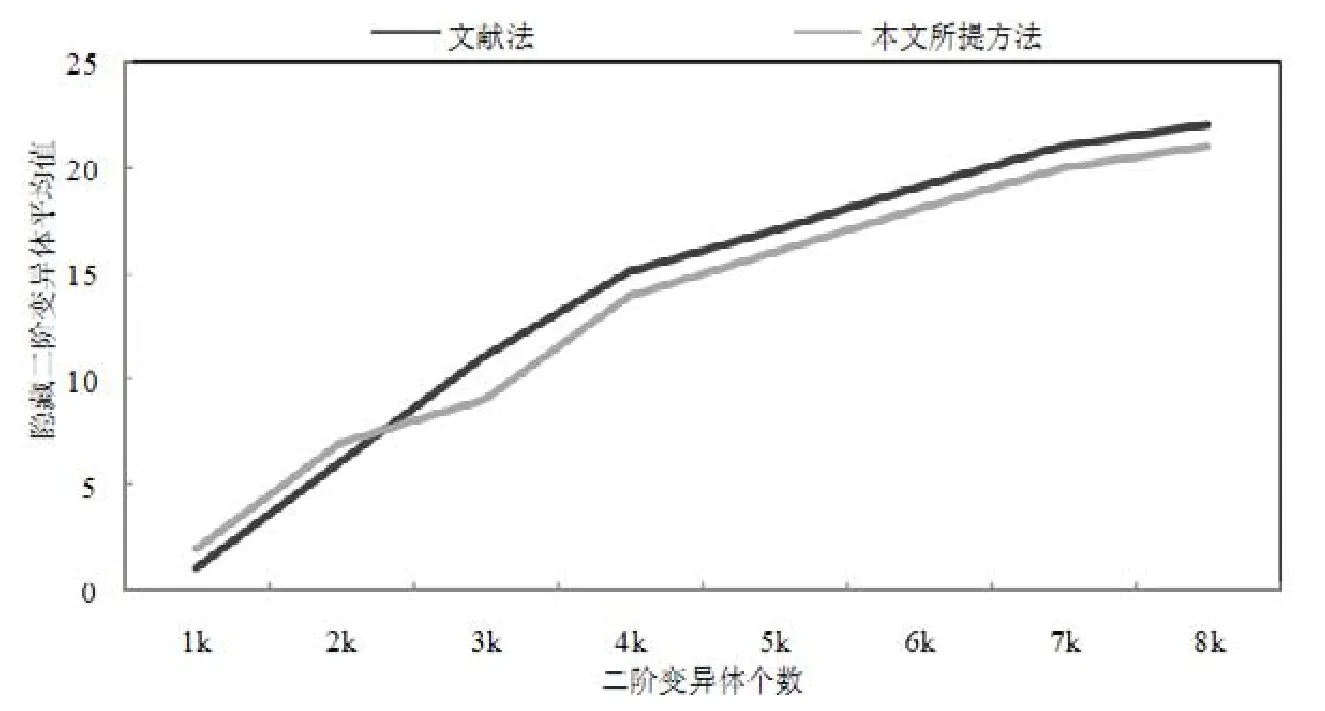
· ROR 表示关系运算符替换,包含 6 个操作符,分别为“<,≤,>,≥,==,≠”.变异点的变异例如“a>b⇒a

· COI表示条件运算符插入,包含一个操作符,即“!”.变异点的变异例如“a≤0⇒!(a≤0)”;

· COR 表示条件运算符替换,包含两个操作符,分别为“&&,||”.变异点的变异例如“(a&&b)⇒(a||b)”;

· AOR表示算术运算符替换,包含5个操作符,分别为“*,/,%,+,-”.变异点的变异例如“(a+b)⇒(a-b).

5.2 实验结果及分析

本文的实验将从以下几个方面开展:所提方法能否减少二阶变异体个数;所提方法对变异充分度是否影响;所提方法能否降低变异测试时间开销;所提方法能否发现隐藏二阶变异体.针对以上几个方面进行如下实验.

(1) 二阶变异体个数的实验

为了验证本文方法能够减少运行的二阶变异体个数.首先用本文方法生成一阶和二阶变异体,通过对一阶和二阶变异体个数的比较,以显示二阶变异体个数的庞大,并和文献[11]方法(记为已有方法)比较.选择该文献的原因如下.

· 首先,该文献中解决的问题和本文所要解决的问题是一致的,即考虑文章中出现的错误组合,然后对二阶变异体个数进行约简;而其他文献中关于高阶变异体的约简则是通过对一阶变异体折半组合以达到减少变异体数量的目的,与本文研究的问题有稍许偏差.

· 其次,该文献作者所在研究组一直跟踪研究高阶变异测试,且该篇文章是该研究组近期发表的一篇非综述类研究高阶变异体约简的文章,该文献的工作具有较好的代表性,所以选其作为对比对象.

实验对比的具体信息见表3.

Table 3 Number of first-order and second-order mutants generated for benchmark programs表3 基准程序生成的一阶和二阶变异体个数

其中,已有方法生成二阶变异体的方法使用的是 Last To First Different Operators策略,该策略忽略了某一个错误组合后再同其他错误组合的情况,造成程序中某些错误组合被遗漏;本文充分考虑程序中可能出现的错误组合,采用较为全面的组合策略对一阶变异体进行组合生成二阶变异体;接着进行聚类前后二阶变异体个数比较的实验,使用二阶变异体减少率的形式展示,具体见表4和表5.

Table 4 Number of second-order mutants after filtering for Mid表4 Mid筛选后的二阶变异体数量

Table 5 Number of second-order mutants after filtering for Triangle表5 Triangle筛选后的二阶变异体数量

如表3所示,为两个程序在本文方法和文献[11]方法下生成的二阶变异体(未筛选)个数.由最后一列可知,与已有方法比,本文方法生成了更多的二阶变异体.如就 Triangle程序而言,已有方法产生的总的二阶变异体的个数为47 557,而本文方法则生成了62 369个二阶变异体,这将有利于充分表示程序中的复杂缺陷.由表4和表5可知,一方面,二阶变异体聚类后个数极少,与聚类前相比减少了很多;另一方面,与已有方法相比,本文方法执行了更少的二阶变异体,如以Triangle为例,已有方法减少了99.86%,而本文方法的减少率至少为99.92%.这表明,基于SOM神经网络的二阶变异体聚类能够有效减少二阶变异体个数.

为了验证结论是否有效,本文对表4和表5中本文方法和已有方法筛选后的减少率做了差异显著性分析(使用的是无重复双因素分析,其中a=0.05),结果见表6.

Table 6 Result of the significance difference analysis of reduction rate of second-order mutants for benchmark programs表6 基准程序中二阶变异体减少率的显著性差异分析的结果

表6从统计学上的显著性差异进行分析,从表格中可以看出,基准程序 Mid和 Triangle的P-value均小于0.01,说明两组数据具备显著性差异的可能性大于 99%,表明本文方法与已有方法的减少率差异极为显著,具有统计学意义上的差异显著性.说明基于SOM神经网络的二阶变异体聚类能够有效减少二阶变异体个数.

(2) 变异充分度的实验

为验证本文方法对变异充分度的影响,首先进行一阶和二阶变异充分度比较的实验,来反映聚类后二阶变异体对变异充分度的影响;然后和文献[11]方法进行变异充分度比较,来反映本文方法的优劣性.实验时使用的一阶变异体和二阶变异体个数的具体信息见表7,变异测试中变异体被杀死的具体信息见表8和表9,变异充分度的比较信息见表10,其中,二阶变异测试充分度计算方法为:假设100个非等价二阶变异体,聚类后有20个簇.若10个簇的代表性二阶变异体被杀死,而10个簇中共含有60个二阶变异体,则变异充分度为60%.

Table 7 Number of mutants under test cases for benchmark programs表7 基准程序的测试例执行的变异体个数

Table 8 Information on the number of first-order mutants killed by executing test cases for benchmark programs表8 基准程序执行测试用例时被杀死的一阶变异体个数的信息

Table 9 Information on the number of second-order mutants killed by executing test cases for benchmark programs表9 基准程序执行测试用例时被杀死的二阶变异体个数的信息

Table 10 Mutation score of first-order and second-order mutation testing for benchmark programs表10 基准程序的一阶和二阶变异测试的变异充分度

表8和表9展示了变异测试中变异体被杀死的具体信息,根据这两个表可得到表10的变异充分度比较信息.其中,本文方法的某个二阶变异体被杀死指该二阶变异体所在簇中的二阶变异体被杀死.以表9中三角形基准程序为例,本文所提方法中被杀死的二阶变异体为12个,则指的是有12个簇的二阶变异体被杀死.

由表10可知,

· 一方面,本文所提方法的二阶变异充分度和一阶变异充分度很接近.以三角形为例,本文方法中二阶变异体的变异充分度为92.5%,较已有文献中的91.7%,更加的接近一阶变异充分度.根据文献[7,11]所述,当二阶变异充分度和一阶变异充分度越接近时,表明二阶变异体选取的越好,即本文选取聚类后的二阶变异体具有很好的效果.

· 另一方面,也表明了本文所提方法取得的二阶变异充分度较文献[11]更接近一阶变异充分度,表明本文所提方法与已有方法相比,能够运行更有效的少量二阶变异体,取得更好的二阶变异充分度.

为了验证该方法的可应用性和有效性,本文使用一个规模较大的开源项目和小组团队开发程序.程序的信息见表11.

Table 11 Information list for practical projects表11 实用项目的信息列表

其中,Snake是一个开源的贪吃蛇游戏,通过键盘上的方向键控制蛇前进的方向,游戏实时记录自己当前的长度及可以计时;Shopping是一个自己小组使用SSH框架开发的电子商城,主要功能有订单管理、用户管理、商品管理.

使用本文提出的组合策略将Snake项目和Shopping项目的一阶变异体组合生成二阶变异体,其中的具体信息见表12.

Table 12 Information of mutants generation for practical projects表12 实用项目的变异体生成的具体信息

由表12中可知,虽然项目代码行较多,但是由于其中多数为不易出错的代码,如Snake中GUI代码,该类代码相似的重复性操作较多(由熟练程序员假设可知,此部分属于不易出错范畴),含操作符代码不多,所以一阶变异体并不多,如Snake一阶变异体数为146个.

因为项目的主要功能分布在某些类中,我们重点对核心类进行分析,实验中,非核心类多数不产生变异体;为验证其可应用性,使用自己团队编写的测试用例进行实验,其中,测试用例并不能保证杀死全部的变异体,选择在全部测试用例下进行分析,而没有再分析单个测试例的变异测试充分度.将聚类前的一阶变异测试充分度和聚类后的二阶变异测试充分度做对比,用以验证本文方法的可应用性.具体信息见表13.

Table 13 Mutation score for practical projects表13 实用项目的变异充分度

由表13可知,两个项目在使用本文方法约简后,二阶变异体测试充分度较一阶变异测试充分度较为接近,如Snake的一阶变异测试充分度为13.68%,其筛选后二阶变异体测试充分度为13.73%.由文献[7,11]可知,当二阶变异充分度和一阶变异充分度接近时,表明二阶变异体约简的效果越好.为验证该结果是否具有统计学上的差异显著性,对实验中的一阶变异测试充分度和筛选后二阶变异测试充分度的数据做差异显著性分析,分析结果见表14.

Table 14 Result of the significant difference analysis of mutation score before and after filtering for practical projects表14 筛选前后的实用项目的变异充分度的显著性差异分析的结果

从表14中可以看出,显著性差异分析结果的P-value为0.894 863,大于0.05,说明两组数据具备显著性差异的可能性小于95%,表明本文方法的筛选后二阶变异充分度较一阶变异测试充分度较为接近.

(3) 时间开销和发现隐藏二阶变异体的实验

因为发现隐藏二阶变异体的实验需知道全部二阶变异体执行过测试例的信息,所以可从聚类后根据符合该特征的簇中获取隐藏二阶变异体.基于该特征,可将发现隐藏二阶变异体和变异体约简的时间开销同时分析.

为了验证本文方法能够降低时间开销,同时便于发现隐藏二阶变异体实验的比较,所以实验中的程序使用基准程序 Coordinate[7],测试例为非充分测试例(即测试组件不能杀死全部二阶变异体),并将本文方法使用的时间和文献[7]中的时间进行比较.

a) 时间开销的实验

本文通过和文献[7]的方法(记为文献法)比较平均时间来反映时间消耗.实验需执行全部的测试组件,而不是执行单独的测试用例进行测试.Coordinate程序的平均时间信息见表15.

Table 15 Average time cost of executing mutants for programs表15 程序执行变异体的平均时间消耗

由表15可知,一方面,虽然聚类花费时间较长,但是聚类后的二阶变异体运行测试例的时间却很短;另一方面,本文中所提方法在发现隐藏二阶变异体功能上,比该文献方法中的时间开销减少了一些,如文献法使用了39 685.000s,而本文方法则使用了38 847.892s.说明本文方法能够减少程序执行开销且用时较少.

b) 发现隐藏二阶变异体的实验

为了验证本文方法能够发现隐藏二阶变异体,实验中每次使用不同个数的算子运用到程序中,生成不同个数的二阶变异体.如图7所示,为该文献方法和本文方法获取到的隐藏二阶变异体的平均数.其中,本文隐藏二阶变异体的获取方法为:根据聚类后的二阶变异体,提取出第一变异体被杀死、第二变异体被杀死,但是二者共同作用时未被杀死的二阶变异体,进行比较,得到隐藏二阶变异体.

Fig.7 Average of finding subtle second-order mutants图7 发现隐藏二阶变异体平均值

由图7可知:

· 本文方法寻找的到隐藏二阶变异体个数的平均数,在总数不是很大时优于该文献.

· 当数据量增大时,与该文献方法几乎一样稍微偏低.原因为数量较大时,根据聚类后的二阶变异体,提取出第一变异体被杀死、第二变异体被杀死,但是二者共同作用时未被杀死的二阶变异体数有少许误差.

综合来说,表明本文方法能够发现隐藏二阶变异体,且数量相差不多.

6 结 论

二阶变异测试中的二阶变异体能够模拟程序中的复杂缺陷,具有重要意义.但由一阶变异体组合形成的二阶变异体数量庞大,因此减少执行的二阶变异体个数、降低程序的执行开销是至关重要的.本文提出了一种基于SOM神经网络的二阶变异体约简方法.

· 首先,采用较为全面的二阶变异体错误组合策略对一阶变异体组合形成二阶变异体;

· 然后,根据二阶变异体执行过程中的中间值相似性,进行基于SOM神经网络模型的变异体聚类;

· 最后,以基准程序和开源项目进行验证.结果表明,组合策略充分模拟了软件中的复杂错误,通过对二阶变异体执行过程中的中间值进行基于 SOM神经网络的聚类,保证了在二阶变异测试充分度较为接近一阶变异充分度的情况下减少了二阶变异测试的执行开销;与此同时,在较短的时间里能够发现隐藏二阶变异体.

另外,二阶变异测试是高阶变异测试的基础,所以该方法可以推广到高阶变异测试中的其他阶的测试.当推广到不同的阶数时,需要另外增加特征属性以达到更好的聚类效果.如果不增加特征属性,也会有一定的聚类效果,但是效果不如现有的方法好,所以需要额外增加特征属性.