基于热传导方程的高温防护服优化模型

王壮 王者 张吉发

摘   要：穿戴高温防护服是防止人在高温作业环境中被灼伤的重要手段。本文对高温防护服传热过程进行分析，在合理简化假设的基础上将此过程转化为一维热传导问题，建立基于一维热传导方程的高温防护服温度分布模型，并确定初始条件、边界条件及耦合条件。为避免求解复杂的偏微分方程，本文采用有限差分法对偏微分方程进行求解。考虑到防护服的实用性及经济性，本文对防护服的厚度进行单目标优化，并采用变步长搜索法对单目标优化模型进行求解。

关键词：热传导方程  有限差分法  变步长搜索  单目标规划

中图分类号：O522                                  文献标识码：A                        文章编号：1674-098X（2019）02（a）-0126-03

Abstract： Wearing thermal protective clothing is an important means to prevent people from being burnt in high temperature working environment. In this paper， the heat transfer process of thermal protective clothing is analyzed. On the basis of reasonable simplifying assumptions， this process is transformed into one-dimensional heat conduction problem. The temperature distribution model of high temperature protective clothing based on one-dimensional heat conduction equation is established， and initial conditions and boundary conditions are determined. Coupling conditions. In order to avoid solving complex partial differential equations， the finite difference method is used to solve the partial differential equations. Considering the practicabili-ty and economy of protective clothing， this paper optimizes the thickness of protective clothing and solves the single objective optimization model by variable step search method.

Key Words： Heat conduction equation; Frinite difference method; Variable step size search; Single objective programming

高温防护服是高温作业人员的重要装备，热防护服不仅要有良好的阻燃性外，还要有较好的隔热性。大量高温环境下的防护服的实验无法重复进行，而且浪费资源，因此研究高温下防护服传热模型是十分重要的。文献[1]建立了多层热防护服的热传递模型，研究了参数最优决定问题。虽然有限元法在处理偏微分方程的边值问题时有一定的优势 ，但在处理热交换边界条件和层状介质的层间热连续条件时往往存在很大的困难。本文将时间空间网格离散化，將热传导方程转化为差分方程，并根据各层交界处的连续性条件列写耦合方程，建立了关于选取的离散点的差分方程组，进行迭代求解，避免了求解复杂的偏微分方程，提高了求解精度和求解速度。本文根据防护服的实际效用与经济成本，建立单目标优化模型，并采用变步长搜索法进行求解。

1  一维热传导非稳态模型

由于本文研究的假人在高温环境中处于静止状态，故可以忽略热对流和热辐射的影响。考虑到防护服各层介质的各向同性，三维传热问题就可简化为一维热传导问题。以防护服与高温环境交界面为轴坐标原点，轴正方向指向假人体内，做出如图1所示的示意图，其中第V层为虚拟的皮肤层。其中防护服各层材料参数如表1所示。

本文将多层防护服等间隔划分77个点（此时d=6mm），对于等间隔的位置节点，将其分为内点，交界点，边界点三类。

1.1 热传导方程

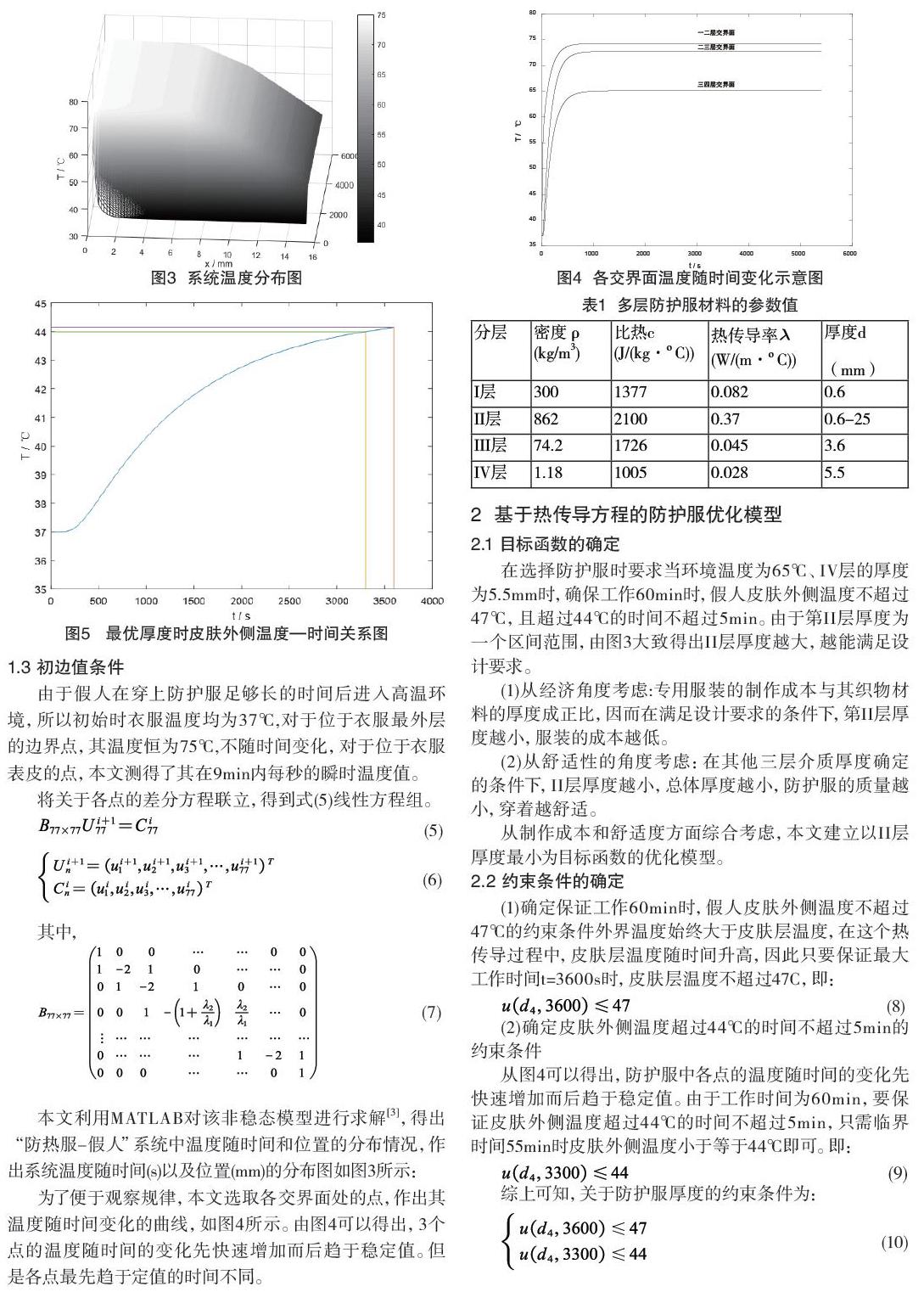
为了便于观察规律，本文选取各交界面处的点，作出其温度随时间变化的曲线，如图4所示。由图4可以得出，3个点的温度随时间的变化先快速增加而后趋于稳定值。但是各点最先趋于定值的时间不同。

2  基于热传导方程的防护服优化模型

2.1 目标函数的确定

在选择防护服时要求当环境温度为65℃、IV层的厚度为5.5mm时，确保工作60min时，假人皮肤外侧温度不超过47℃，且超过44℃的时间不超过5min。由于第II层厚度为一个区间范围，由图3大致得出II层厚度越大，越能满足设计要求。

（1）从经济角度考虑：专用服装的制作成本与其织物材料的厚度成正比，因而在满足设计要求的条件下，第II层厚度越小，服装的成本越低。

（2）从舒适性的角度考虑：在其他三层介质厚度确定的条件下，II层厚度越小，总体厚度越小，防护服的质量越小，穿着越舒适。

从制作成本和舒适度方面综合考虑，本文建立以II层厚度最小为目标函数的优化模型。

2.2 约束条件的确定

3  结语

本文合理简化假设将时间空间网格离散化，针对高温防护服传热过程建立起基于一维热传导方程的非稳态温度分布模型。在此模型的基础上本文对高温防护服的厚度进行单目标优化，建立优化模型并利用变步长搜索算法使用MATLAB求解，该模型具有较高的实用性和推广性。本文为降低高温防护服研发成本、缩短研发周期提供了理论依据，但本文的算法设计仍具有一定的误差需进一步优化设计。

参考文献

[1] 卢琳珍.多层热防护服装的热传递模型及参数最优决定[D].浙江理工大学，2018.

[2] 杨世铭，陶文铨.传热学[M].4版.北京：高等教育出版社，2006.

[3] 史策.热传导方程有限差分法的MATLAB实现[J].咸阳师范学院报，2009，24（4）：27-29.

[4] 姜启源，谢金星，叶俊.数学模型[M].3版. 北京：高等教育出版社，2003.