基于改进迟滞阻尼模型的混合结构抗震分析SRSS法

孙攀旭 杨红 刘庆林

摘 要：混合结构的阻尼矩阵不再满足经典阻尼条件，无法直接采用模态叠加法。迟滞阻尼模型具有每周期耗散能量与外激励频率无关的优点，且时域计算结果稳定收敛，但不满足能量守恒原则。利用结构每周期耗散能量与阻尼做功相等，对迟滞阻尼模型的阻尼系数进行修正，得到了改进迟滞阻尼模型，并提出了对应的混合结构模态叠加法。在此基础上，分析改进迟滞阻尼模型的反应谱特点，计算最不利地震作用效应组合，提出了基于改进迟滞阻尼理论的混合结构抗震分析SRSS法。算例分析表明，改进迟滞阻尼模型计算的地震作用效应比粘性阻尼模型计算的地震作用效应更大，其增大幅度约为15%～20%。

关键词：混合结构;迟滞阻尼;模态叠加法;反应谱;SRSS

中图分类号：TU311.3

文献标志码：A  文章编号：2096-6717（2019）02-0093-06

Abstract：Damping matrix of mixed structure no longer satisfies the classical damping condition. In such a case， the modal superposition method may become invalid. The advantage of hysteretic damping model is that energy consumption is related to external excitation frequencies in each cycle. At the same time， the calculation results of time-domain are stable. However， it does not meet the principle of energy conservation. By the equivalence of energy dissipation and damping power in each cycle， damping coefficient of hysteresis damping model can be modified. Subsequently， an improved hysteretic damping model and its own modal superposition method of mixed structure are proposed in this paper. The characteristics of improved hysteretic damping model response spectrum are firstly analyzed. Then， the most unfavorable combination of seismic effects could be calculated. Based on the improved hysteretic damping model， SRSS method for seismic analysis of mixed structure is performed. Results show that seismic effects of the improved hysteretic damping model are more significant than that of viscous damping model， and the increase is about 15%～20%.

Keywords：mixed structure; hysteretic damping; modal superposition method; response spectrum; SRSS

混合結构的地震响应计算方法与单一材料结构采用的常用方法不同。由于不同材料的阻尼比不同，混合结构的阻尼矩阵并不与质量矩阵或刚度矩阵保持比例关系，故混合结构无法直接采用基于粘性阻尼模型的实模态叠加法，抗震计算时也无法直接采用SRSS法。

目前，常用的阻尼模型为粘性阻尼模型和复阻尼模型[1]。对于混合结构，选择结构的重要振型，可得到相应的Rayleigh阻尼矩阵，进而实现模态叠加法[2-4]，但其结果不具有唯一性，高阶振型地震作用效应亦偏小[5];采用等效阻尼比的思路，将阻尼矩阵等价为比例矩阵，同样可实现模态叠加法[6-7]，但计算出局部结构的地震效应偏小或偏大[8];汪梦甫[9]、Neugebauer等[10-11]利用状态空间法，提出了基于粘性阻尼模型的复模态叠加法，但矩阵维度增加了一倍，计算量较大;刘庆林等[12]基于复阻尼模型的复模态叠加法可直接适用于混合结构，但计算较为复杂，且直接剔除复阻尼运动方程通解中发散项的做法存在理论缺陷[13]。Wang[14]采用Rayleigh阻尼矩阵等效复阻尼矩阵，Reggio等[15]将Maxwell-Wiechert本构模型等效于复阻尼本构模型，进而解决了发散问题，但上述方法得到的计算结果与复阻尼理论存在一定的误差。迟滞阻尼模型计算结果唯一，且克服了粘性阻尼模型中每周期耗散能量与外激励频率相关的缺点。同时，迟滞阻尼模型的时域计算结果稳定收敛，避免了复阻尼模型的发散现象[16]。

迟滞阻尼模型克服了粘性阻尼模型和复阻尼模型的缺陷，但不满足能量守恒的原则。本文利用结构每周期耗散能量与阻尼做功相等的特性，对迟滞阻尼模型的阻尼系数进行修正，得到改进迟滞阻尼模型，并提出了对应的混合结构模态叠加法。同时，分析改进迟滞阻尼模型的反应谱特点，计算最不利地震作用效应组合，并提出了基于改进迟滞阻尼模型的混合结构抗震分析SRSS法。

1 基于改进迟滞阻尼模型的SRSS法

1.1 改进迟滞阻尼模型

迟滞阻尼模型假定阻尼力与结构的位移大小成正比，与结构的速度方向相反[16-17]。单自由度体系的迟滞阻尼运动方程为

由式（15）可计算出对应的自振频率和特征向量，采用改进迟滞阻尼模型时，Kf可视为结构的动态刚度矩阵，结构的振动过程将是刚度不断变化的过程。由式（15）可知，方程的特征值和特征向量不仅与结构的质量、刚度和阻尼有关，还与运动过程中的符号矩阵有关。对于n自由度结构，符号矩阵的个数为2n，因此，需要计算对应的2n个特征值和特征向量。当符号矩阵确定时，利用每个符号矩阵对应的特征向量，可对式（11）进行解耦计算，进而实现改进迟滞阻尼模型的模态叠加法。

利用特征向量和加速度反应谱，可计算每个符号矩阵对应下的地震作用效应，但为了保证结构设计的安全性，用于设计的地震作用效应须选择最不利情况，即多种地震作用效应中的最大值，从而可实现改进迟滞阻尼模型的抗震分析SRRS法。

2 基于改进迟滞阻尼模型的加速度反应谱

采用改进迟滞阻尼模型时，单自由度体系的时域积分计算仍按照时间步长Δt进行离散，任意时刻可表示为tk=kΔt（k=0，1，2…）。当Δt取值足够小时，可利用tk时刻结构的动力响应确定tk+1时刻的符号矩阵，并得到tk+1时刻的运动方程，由此进行时域迭代计算。利用单自由度的加速度响应，可得到基于改进迟滞阻尼模型的加速度反应谱。

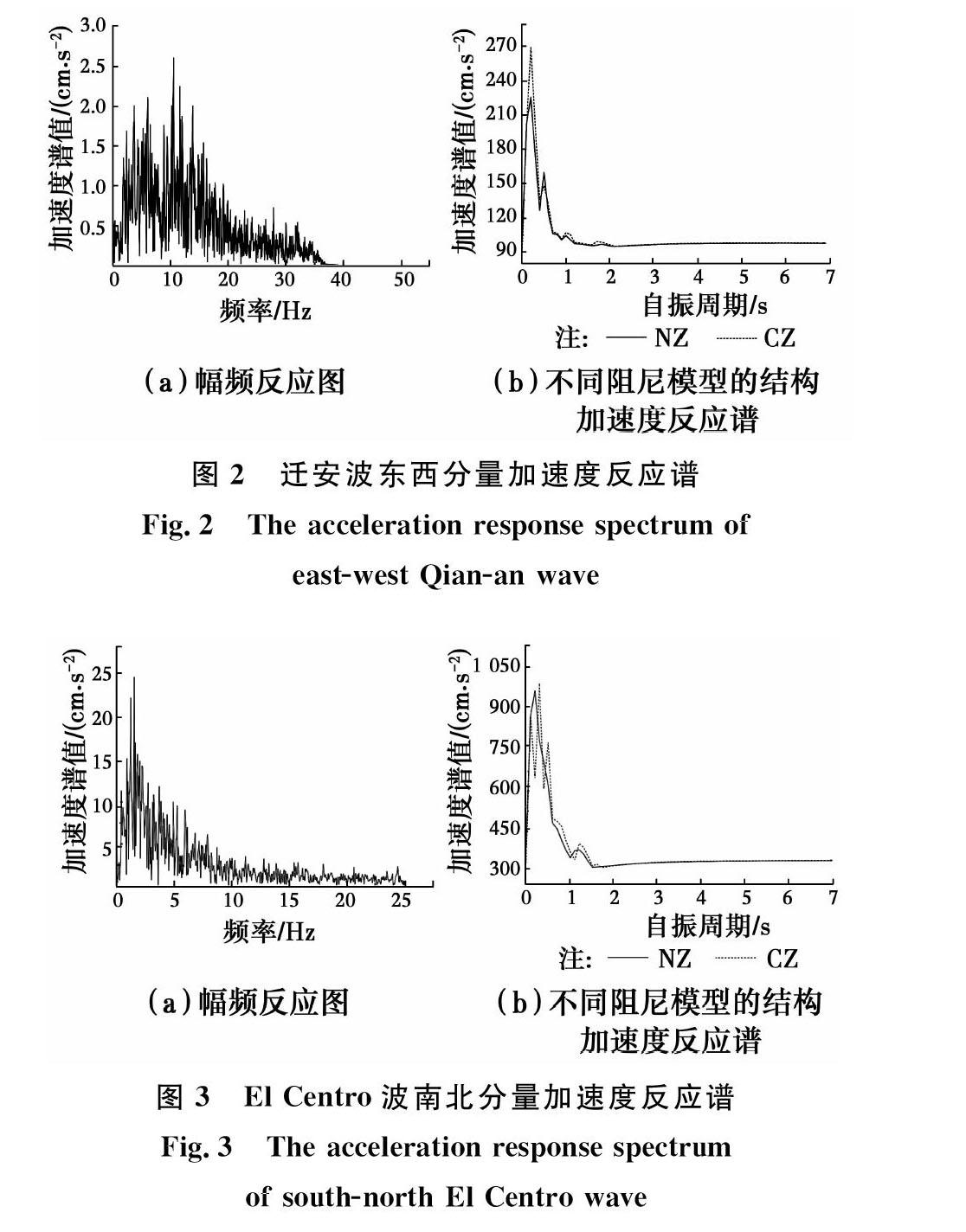
加速度反应谱是结构抗震分析SRSS法的重要依据。以两条地震波为例，分析了改进迟滞阻尼模型加速度反应谱和粘性阻尼模型反应谱之间的差异。

在图2和图3中，计算所得的两条地震波作用下改进迟滞阻尼模型（CZ）的加速度谱值和粘性阻尼模型（NZ）的加速度谱值表明：在短周期段，CZ计算的加速度谱值小于NZ计算结果;在中周期段和长周期段，CZ计算的加速度谱值大于NZ计算结果。

由于本文的重点在于研究迟滞阻尼理论的改进以及混合结构SRSS法的实现方法，对于迟滞阻尼理论反应谱的深入分析以及两种阻尼模型对应的设计反应谱的差异和对地震响应计算结果的影响，有待后续研究进一步澄清。与此同时，考虑到基于粘性阻尼理论的规范设计反应谱存在人为抬高拉平的做法[18]，故在后续算例中采用改进迟滞阻尼模型进行SRSS计算时，仍暂时借用规范的设计反应谱。

3 算例分析

如图4所示，以不同材料组成的3层剪切型框架结构为例，其具体参数为：抗震设防烈度为8度，设计基本地震加速度为0.20g，设计地震分组为第2组，场地类别为II类，钢结构的阻尼比为0.02，钢筋混凝土结构的阻尼比为0.05。

对于3层框架，其符号矩阵共有8个，因此，需要计算每个符号矩阵对应运动方程下的框架层间剪力。如上文所述，基于改进迟滞阻尼模型的SRSS法可暂时采用规范反应谱，据此可计算出8个符号矩阵对应下的层间剪力，其结果如表1和图5所示。

在图5中，绘制了层间剪力的散点图，可得到最大剪力包络线，即选择最不利地震作用效应组合，从而计算出改进迟滞阻尼模型下的框架层间剪力。

混合结构基于粘性阻尼模型的SRSS法可采用等效阻尼比ξd计算层间剪力。选择等效阻尼比时，若直接取阻尼比的平均值，可得等效阻尼比为0.035;若采用复頻率法[6]确定混合结构振型阻尼比，将质量参与系数作为权系数进行加权平均，得到的混合结构等效阻尼比为0.038 9。分别采用粘性阻尼模型的SRSS法（NZ_SRSS）和改进迟滞阻尼模型的SRSS法（CZ_SRSS）计算框架的层间剪力，其结果见表2。

CZ_SRSS的计算结果较NZ_SRSS（ξd=0.035）计算的层间剪力增加幅度为14.81%～16.75%，表明CZ_SRSS的计算结果普遍较大，且顶层剪力增幅最大，达到16.75%;CZ_SRSS的计算结果较NZ_SRSS（ξd=0.038 9）计算的层间剪力增加幅度为16.92%～19.14%，其增幅规律类似，且顶层剪力增幅达到19.14%。

对于N层剪切型框架，第k层结构在符号矩阵中对应的对角元素为1，其他层结构对应的对角元素为-1，即

τ 此时，相比粘性阻尼模型下原结构的刚度分布情况，第k层结构对应的刚度增大，其他层对应的刚度减小，进而导致计算结果中第k层结构对应的地震作用效应增大。

基于改进迟滞阻尼模型的SRSS法选择每个符号矩阵对应下的最大地震作用效应，进而形成最不利地震作用效应组合，使得改进迟滞阻尼模型计算的地震作用效应大于粘性阻尼模型。

4 结论

经理论推导和算例分析，得以下结论：

1）改进迟滞阻尼模型具有每周期耗散能量与外激励频率无关的优点，但改进迟滞阻尼系统不再保持线性特征，具有局部的非线性特征。

2）与粘性阻尼模型相比，基于改进迟滞阻尼模型的模态叠加法可适用于非比例阻尼矩阵的混合结构。

3）基于改进迟滞阻尼模型的混合结构抗震分析SRSS法需要计算每种符号矩阵下的地震作用效应，计算量相对较大;若选择最不利地震作用效应组合，改进迟滞阻尼模型计算的地震作用效应比粘性阻尼模型计算的地震作用效应更大，其增大幅度约为15%～20%。

参考文献：

[1] 梁超锋， 刘铁军， 邹笃建，等. 材料黏滞系数与损耗因子的频率相关性研究[J]. 力学学报， 2012， 44（5）： 933-937.

LIANG C F， LIU T J， ZOU D J， et al. The frequency-dependent study on viscosity coefficient and loss tangent of viscoelastic materials [J]. Chinese Journal of Theoretical and Applied Mechanics， 2012， 44（5）： 933-937. （in Chinese）

[2] 潘旦光，高莉莉. Rayleigh阻尼系数解法比较及对结构地震反应影响[J]. 工程力学，2015，32（6）： 192-199.

PAN D G， GAO L L. Comparison of determination methods for Rayleigh damping coefficients and effects on seismic responses of structures [J]. Engineering Mechanics， 2015， 32（6）： 192-199. （in Chinese）

[3] 黄维，钱江，周知. 基于Rayleigh阻尼模型的竖向混合结构设计阻尼比研究[J].工程力学，2015， 32（10）： 60-67.

HUANG W， QIAN J， ZHOU Z. Research on equivalent damping ratio of vertically mixed structures based on Rayleigh damping model [J]. Engineering Mechanics， 2015， 32（10）： 60-67.（in Chinese）

[4] HUANG W， QIAN J， ZHOU Z， et al. An approach to equivalent damping ratio of vertically mixed structures based on response error minimization [J]. Soil Dynamics and Earthquake Engineering， 2015， 72： 119-128.

[5] 刘庆林，傅学怡. 基于复阻尼假定的不同材料阻尼特性混合结构抗震分析反应谱CCQC法[J]. 土木工程学报，2011， 44（3）： 61-71.

LIU Q L， FU X Y. A response spectrum CCQC method for seismic analysis of structures of multiple material damping characteristics based on complex damping assumption [J]. China Civil Engineering Journal， 2011， 44（3）： 61-71. （in Chinese）

[6] 黃本才. 组合结构振动的等效阻尼比[J]. 上海力学，1998， 19（2）：141-145.

HUANG B C. Equivalent modal damping ratios of vibration in composite structures [J]. Shanghai Journal of Mechanics， 1998， 19（2）：141-145. （in Chinese）

[7] 薛彦涛，韦承基，孙仁范，等. 采用不同材料加层时结构阻尼比计算方法（应变能法）[J]. 工程抗震与加固改造， 2008， 30（2）： 91-95.

XUE Y T， WEI C J， SUN R F， et al. Calculation method for damping ration of different story added structures （strain energy method） [J]. Earthquake Resistant Engineering and Retrofitting， 2008， 30（2）： 91-95. （in Chinese）

[8] 梁仁杰，吴京，孟少平. 能力谱法中等效阻尼比的误差分析及假设检验[J]. 土木工程学报，2010， 43（Sup1）： 33-36.

LIANG R J， WU J， MENG S P. Error analysis and assumption test on the equivalent damping ratio in capacity spectrum method [J]. China Civil Engineering Journal， 2010， 43（Sup1）： 33-36. （in Chinese）

[9] 汪梦甫. 非比例阻尼线性体系地震反应计算的振型分解反应谱法[J]. 地震工程与工程振动，2007， 27（1）： 31-37.

WANG M F. On seismic response analysis methods of non-proportional damped linear MDOF systems [J]. Journal of Earthquake Engineering and Engineering Vibration， 2007， 27（1）： 31-37. （in Chinese）

[10] NEUGEBAUER R， SCHEFFLER C， WABNER M， et al. Advanced state space modeling of non-proportional damped machine tool mechanics [J]. CIRP Journal of Manufacturing Science and Technology， 2010， 3（1）： 8-13.

[11] NEUGEBAUER R， SCHEFFLER C， WABNER M， et al. State space modeling of non-proportional passive damping in machine tools [J]. The International Journal of Advanced Manufacturing Technology， 2011， 53： 945-952.

[12] 刘庆林，傅学怡，孙占琦. 基于复阻尼假定的不同材料阻尼特性混合结构抗震分析复模态叠加法[J]. 建筑结构学报，2011， 32（9）： 27-33.

LIU Q L， FU X Y， SUN Z Q. A complex mode superposition method for seismic analysis of structures of multiple material damping characteristics based on complex damping assumption [J]. Journal of Building Structures， 2011， 32（9）：27-33. （in Chinese）

[13] 何钟怡，廖振鹏，王小华. 关于复阻尼理论的几点注记[J]. 地震工程与工程振动，2002，22（1）： 1-6.

HE Z Y， LIAO Z P， WANG X H. Some notes on theory of complex damping [J]. Earthquake Engineering and Engineering Vibration， 2002， 22（1）： 1-6. （in Chinese）

[14] WANG J. Rayleigh coefficients for series infrastructure systems with multiple damping properties [J]. Journal of Vibration and Control， 2015， 21（6）： 1234-1248.

[15] REGGIO A， DE ANGELIS M. Modelling and identification of structures with rate-independent linear damping [J]. Meccanica， 2015， 50（3）： 617-632.

[16] CHEN L Y， CHEN J T， CHEN C H， et al. Free vibration of a SDOF system with hysteretic damping [J]. Mechanics Research Communications， 1994， 21（6）： 599-604.

[17] 朱镜清. 频率相关粘性阻尼理论及有关问题的解[J]. 振动与冲击，1992，11（4）：1-7.

ZHU J Q. Frequency dependant viscous damping theory and some related problems [J]. Journal of Vibration and Shock， 1992，11（4）：1-7. （in Chinese）

[18] 朱鏡清，朱敏. 复阻尼地震反应谱的计算方法及其它[J]. 地震工程与工程振动，2000， 20（2）： 19-23.

ZHU J Q， ZHU M. Calculation of complex damping response spectra from earthquake records [J]. Earthquake Engineering and Engineering Vibration， 2000， 20（2）： 19-23. （in Chinese）

（编辑 王秀玲）