偏差改正的Partial EIV模型方差分量估计

王乐洋，温贵森

1. 东华理工大学测绘工程学院，江西 南昌 330013； 2. 流域生态与地理环境监测国家测绘地理信息局重点实验室，江西 南昌 330013； 3. 江西省数字国土重点实验室，江西 南昌 330013

在测量数据处理中，Gauss-Markov模型是常用的平差模型，模型解算常用的方法为最小二乘方法。然而在某些实际情况中，Gauss-Markov模型系数矩阵A的元素可能由某些含有观测误差的观测值构成，此时经典的最小二乘平差方法不够严密。总体最小二乘[1-4]是同时顾及了观测向量与系数矩阵误差的平差方法，是变量误差(errors-in-variables，EIV)模型的严密估计方法。文献[5—7]研究了总体最小二乘的迭代算法；文献[8—14]研究了附有等式约束和不等式约束条件的总体最小二乘方法；文献[15]研究了提高计算效率的总体最小二乘方法。部分变量误差[16](partial error-in-variables，Partial EIV)模型是考虑了EIV模型系数矩阵中存在随机元素和非随机元素的情况，相比于EIV模型，Partial EIV模型更具有一般性和适用性，且在算法及应用中都得到了广泛的研究[17-25]。

由于EIV模型或Partial EIV模型受非线性的影响，总体最小二乘解算得到的参数估值及单位权方差估值是有偏的[26-27]。文献[28]分析了系数矩阵误差对EIV模型平差参数估值的影响。文献[29]基于泰勒公式展开的二次项，得到了非线性函数的偏差公式。文献[30]基于EIV模型，通过线性化处理得到了参数估值及参数估值一阶近似协方差阵。文献[27]对迭代的最后一步表达式进行线性化，得到了参数估值的一阶近似协方差阵。文献[16]根据非线性理论得到了参数估值偏差及一阶近似协方差阵。文献[31]通过迭代计算得到参数估值的协方差阵。文献[32]推导了多元总体最小二乘算法并得到了参数估值的一阶近似协方差阵。以上计算方法及通过协方差传播得到的参数估值方差只计算到一阶近似。文献[33]使用SUT(scaled unscented transformation)方法计算得到总体最小二乘参数估值的二阶近似协方差阵。文献[34]推导了总体最小二乘精度评定的二阶近似函数法，将参数估值精度提高至二阶，进一步完善了总体最小二乘精度评定理论。

方差分量估计[35-39]是针对随机模型不准确从而对权进行修正的验后估计方法，方差分量估计方法通过预平差得到的信息根据一定的原则对观测量的验前方差或协方差进行估计、重新定权。文献[40]分析了EIV模型的最小二乘方差分量估计。文献[41]引入权修正因子，推导了Partial EIV模型的Helmert方差分量估计。文献[42]得到了Partial EIV模型的非负最小二乘方差分量估计；然而以上总体最小二乘方差分量估计方法中并未考虑参数估值有偏性的影响。文献[43]推导了EIV模型的最小范数二次无偏估计，分析了由参数估值偏差引起的方差分量估值的偏差，推导了方差分量估值偏差的表达式。

基于上述分析，本文考虑总体最小二乘估计参数估值的偏差，进行偏差改正得到偏差改正后的参数估值，更新由参数估值引起变化的中间变量，将偏差改正与方差分量归为整体同时迭代计算，进行偏差改正后的方差分量估计及二阶精度评定。通过算例试验，将偏差改正后得到的结果与未进行偏差改正的结果进行对比分析，验证本文方法的可行性。

1 Partial EIV模型参数偏差及精度评定

1.1 Partial EIV模型解算

针对EIV模型系数矩阵中存在固定元素及重复出现的随机元素，文献[16]将系数矩阵中的随机元素分离，提出了Partial EIV模型，其数学模型为

函数模型

(1)

随机模型

(2)

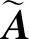
目前针对Partial EIV模型的解法较多，本文参考文献[19]的求解思路，构造拉格朗日条件极值函数

Φ=eTQ-1e+2λT(y-(βT⊗In)(h+Ba)+Ce)

(3)

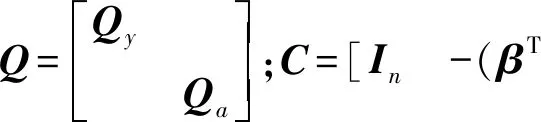
对式(3)进行解算最终可得到参数估值的表达式为

(4)

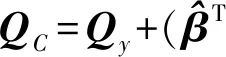
(5)

由于总体最小二乘方法顾及了系数矩阵误差，式(1)可以看作为非线性模型，Partial EIV模型解算得到的参数是有偏或近似无偏的[16]。将Partial EIV模型视为非线性模型得到

e=f(x)-l

(6)

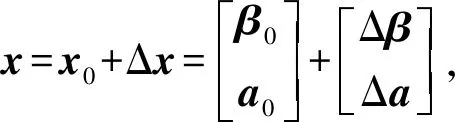
(7)

(8)

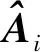
(9)

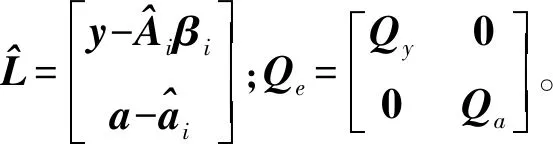
通过迭代计算最终得到参数估值为

(10)

式(4)与式(10)是等价的，通过迭代计算都能得到相同的参数估值。

1.2 基于二阶导数的偏差计算及精度评定

文献[16]针对Partial EIV模型的非线性推导了参数估值的偏差表达式及参数估值的一阶近似协方差阵。参数估值偏差表达式和协方差表达式分别为[16]

(11)

(12)

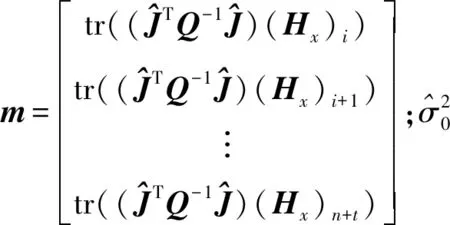
同理，式(4)通过协方差传播律可以得到参数估值的一阶近似协方差

(13)

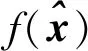
(14)

(15)

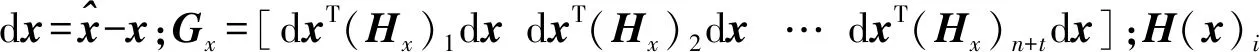
(16)

(17)

式(15)可以得到参数估值的偏差

(18)

进而可以得到偏差改正后的参数估值

(19)

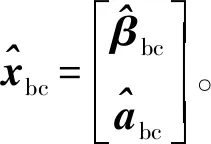
(20)

2 基于偏差改正的方差分量估计

随机模型的验后估计又称方差分量估计，是针对平差前给定的随机模型不准确而提出的方法。方差分量估计的基本思想是先对各类观测值定初权，进行预平差，利用预平差后得到的信息，主要是各类观测值的改正数，并根据得到的观测值的改正数对各类观测值的验前方差和协方差进行估计，重新定权。

考虑式(2)随机模型形式为

(21)

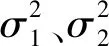
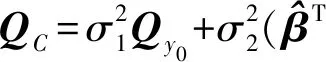
(22)

对总体最小二乘解算可以得到

(23)

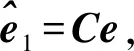
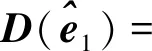
(24)

式中，p在本文中取值为2，Qk的形式为

(25)

式中，k=1时，表示观测量y对应的初始协因数阵；k=2时，表示系数矩阵对应的初始协因数阵。

本文以最小二乘方差分量估计方法为例，文献[40]分析了总体最小二乘的最小二乘方差分量估计，将方差分量作为参数进行最小二乘平差解算得到

(26)

式中，vh表示取出对称矩阵的上三角元素按照一定的顺序排列成列向量。

文献[36]通过公式转换得到法矩阵N和列向量L的形式为

(27)

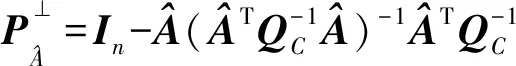
针对Partial EIV模型式(1)，模型的总观测量个数为n+t，必要观测量个数为t+m，在平差计算时是将系数矩阵含有观测误差的数据作为参数进行解算；根据非线性解算理论，参数β与系数矩阵观测值a组成的向量x在进行式(10)的迭代计算时是存在偏差的，而参数估值影响观测值改正数，从而影响方差分量估计。将偏差改正后的参数估值代入方差分量估计中，即存在

(28)

继而有

(29)

式中，下标bc表示偏差改正后对应的值。

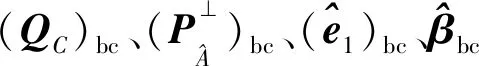
(30a)

进而得到

(30b)

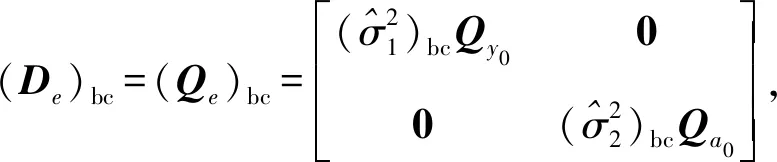
(31a)

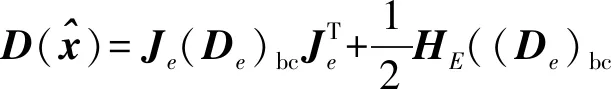
(31b)

将参数估值偏差改正与方差分量估计作为一个整体进行迭代计算，其迭代流程见图1。

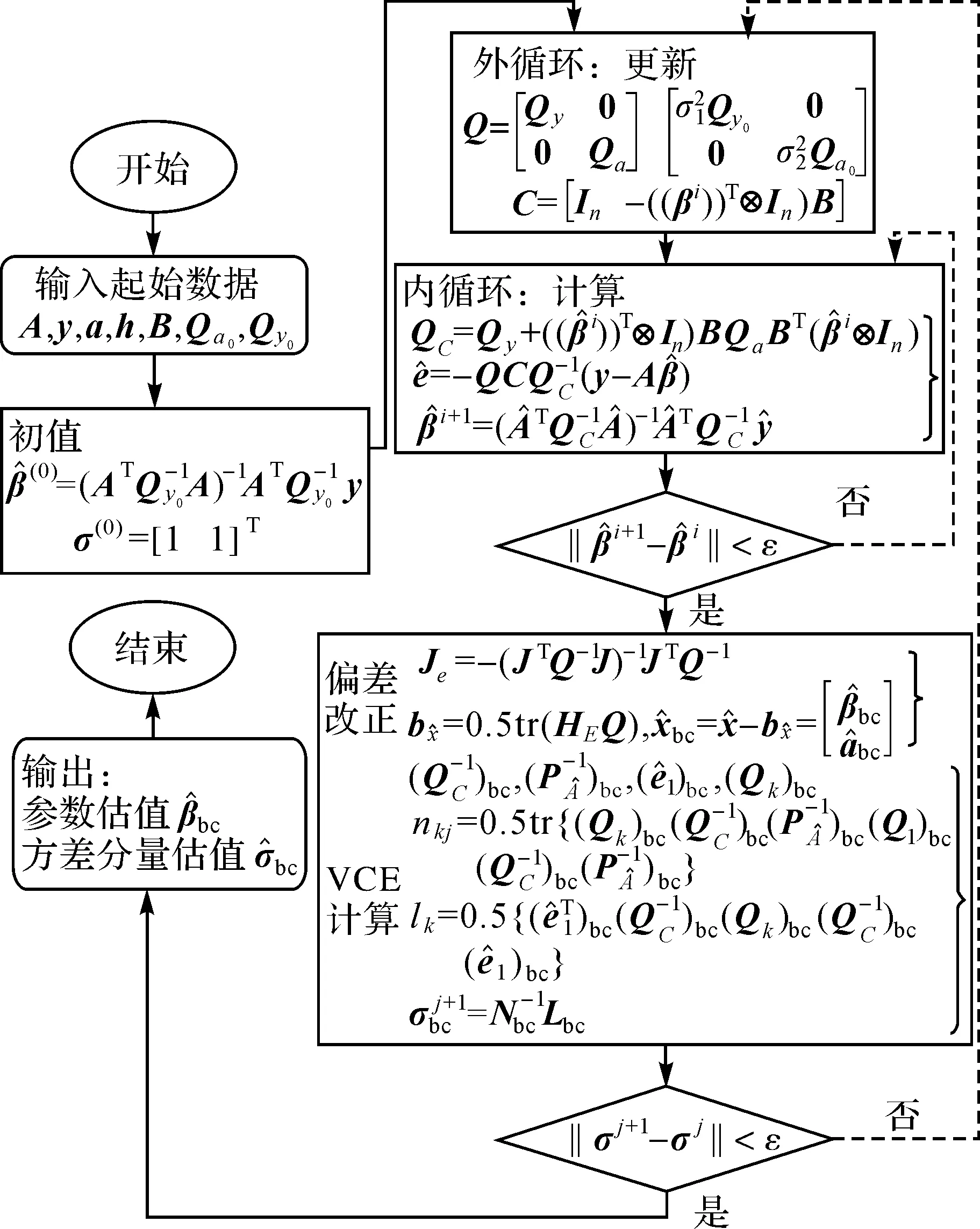
图1 偏差改正方差分量估计迭代流程Fig.1 Flow chart of bias correction variance components estimation iteration

3 算例与分析

3.1 算例1 直线拟合

采用文献[18]的数据，直线拟合的模型为

(32)

已知坐标观测值(xi,yi)和相应的权值(pxi,pyi)，见表1。

考虑观测数据的个数，构造Partial EIV模型的向量h与矩阵B的形式为

(33)

现分别使用最小二乘(LS)、总体最小二乘(TLS)、总体最小二乘的最小二乘方差分量估计方法[40](TLS-VCE)及本文方法(偏差改正的方差分量估计)计算，得到的参数估值、参数估值偏差及方差分量估值结果见表2。

表1 坐标观测值及相应的权值[18]

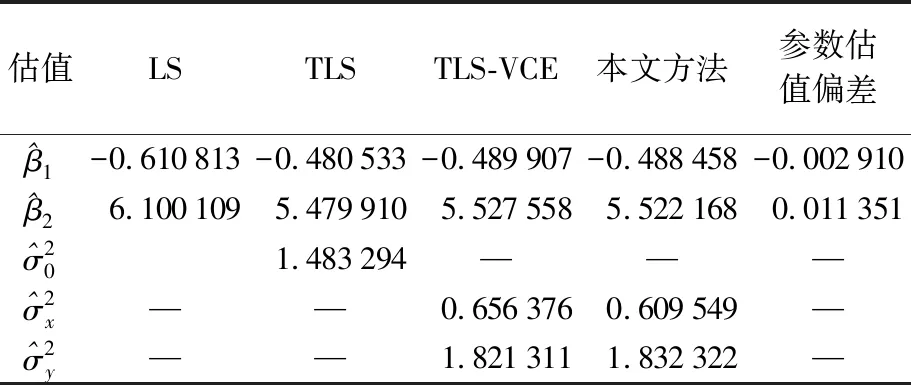
表2 算例1不同方法得到的参数估值、参数估值偏差及方差分量估值

从表2可以看出，经过偏差改正后的方差分量估计得到的方差分量估值及参数估值都有所改变，这主要是由参数估值的偏差引起的，参数估值偏差越大，对结果的影响也越大。计算得到参数估值的标准差结果见表3。

表3 算例1参数估值的标准差

3.2 算例2 二维仿射变换

根据文献[38—39]算例思想，在长宽为100 m的正方形区域内，沿纵横坐标方向每隔10 m选取一个点，共121个点，在正方形区域的所有点中均匀选取31个点作为公共点进行二维仿射变换。二维仿射变换模型可以表示为

(34)

式中，Δx、Δy为平移参数；ωx、ωy为旋转参数；kx、ky为尺度参数；(xi，yi)、(Xi，Xi)分别为第i个公共点的原始坐标系及目标坐标系的坐标。

将式(34)改写成矩阵形式得到

(35)

式中，a1=kxcosωx；b1=kysinωy；a2=-kxsinωx；b2=kycosωy，构造Partial EIV模型的向量h与矩阵B的形式为

(36)

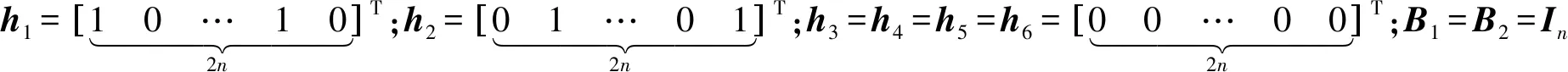
给定一组转换参数真值，Δx=Δy=0，ωx=100，ωy=110，kx=1.01，ky=1.02，假设目标坐标系坐标之间相互独立且等精度，原始坐标同一点中x、y坐标独立，不同点间坐标相关，对应协因数阵中非对角线元素为

(37)

式中，qij为协因数阵中对应的元素值；dij为i、j点间的距离；d0为常数且取值为10 m。

现分别给原始坐标与目标坐标模拟均值为0，服从正态分布的随机误差。其中，原始坐标单位权中误差为1 cm，目标坐标单位权中误差为3 cm。分别使用最小二乘(LS)、总体最小二乘(TLS)、总体最小二乘的最小二乘方差分量估计[40](TLS-VCE)及本文方法计算，得到的参数估值、参数估值偏差及参数估值与真值的差值范数见表4。

表4 算例2不同方法得到的参数估值、偏差及差值范数

从表4可以看出，由于该算例中参数估值偏差较小，不同方法得到的参数估值相差较小，参数估值与真值的差值范数也较小，但方差分量估计方法可以得到与平差前给定的方差分量相近的估值；计算得到原始坐标与目标坐标的方差分量估值见表5。

表5 算例2原始坐标与目标坐标方差分量估值

从表5可以看出，方差分量估计方法得到原始坐标的观测精度为2.994 689 cm，目标坐标的观测精度为1.142 152 cm，与平差前给定的3 cm和1 cm接近；而由于该算例中参数估值偏差较小，经过偏差改正后的方差分量估值与未经过偏差改正的相差较小，但都接近于验前给定的方差分量。

3.3 算例3 四参数坐标转换

在算例2中，由于观测量误差较小，在构造总体最小二乘平差模型时，系数矩阵误差很小，TLS与LS结果相差较小；文献[28]指出系数矩阵的信噪比达到一定量级时，参数估值的相对偏差很小，LS与TLS结果必然没有差别。考虑一个四参数坐标转换模型

(38)

根据所提供坐标个数，得到向量h、B形式如下

(39)

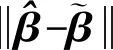
表6 算例3坐标观测值及协因数

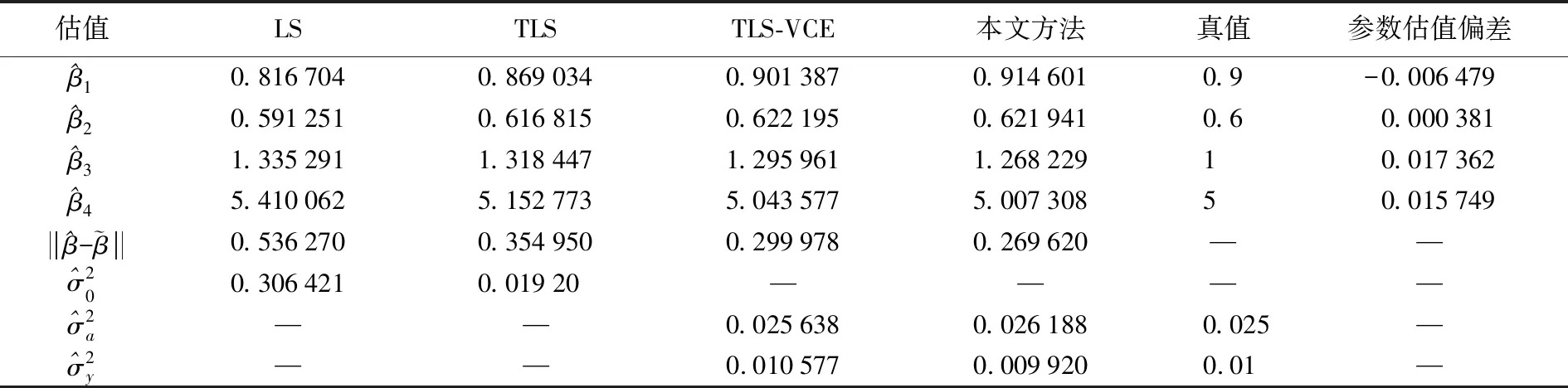
表7 算例3不同方法得到参数估值、偏差及方差分量估值

从表7与表8可以看出，方差分量估计方法可以得到与平差前相近的方差分量，对参数估值也有修正作用，而加入偏差改正后的方差分量估计方法得到的参数估值与真值的差值范数最小，数值为0.269 620，更接近于参数真值。

3.4 算例分析

(1) 算例1中，方差分量估计方法可以得到不同类数据的方差分量估值，而考虑总体最小二乘参数估值的有偏性时，对参数估值进行偏差改正，将改正后的参数估值与方差分量估计结合成整体进行计算，可以得到修正后的参数估值与方差分量估值。方差分量估值影响参数估值的精度评定，从表3的参数估值标准差可以看出，偏差改正后的参数估值标准差小于未偏差改正的参数估值标准差，而二阶方差在数值上要大于一阶，说明在非线性模型的精度评定时应尽可能考虑线性化过程中舍去的高次项信息。

(2) 算例2中，由于观测数据的量级与观测误差的量级差别较大，系数矩阵误差对平差结果的影响较小，相应地将平差模型作为非线性模型时，得到的参数估值偏差很小，量级为10-7，表4所提供的参数估值结果都与LS结果相差较小；表5中方差分量估计方法都可以得到接近于平差前给定的方差分量，说明了方差分量估计方法的有效性；而由于参数估值偏差较小的原因，经过偏差改正后得到的方差分量估值与未经过偏差改正得到的方差分量估值接近一致，这也说明偏差大小与数据初始精度及模型的非线性强度有关[44]。

(3) 算例3中，考虑观测数据量级较小且观测量的方差较大的四参数坐标转换模型，表7中给出计算得到参数估值的偏差最大为0.017 362，参数的偏差百分比为1.34%，模型具有非线性形态且有必要考虑泰勒展开式的二阶项[44]，表7提供的参数估值与真值的差值范数中，经过偏差改正后的方差分量估计得到的参数估值最接近于真值，相比于不考虑偏差改正的方差分量估计方法，更说明了偏差改正的必要性；从表8中的参数估值标准差可以看出，加入偏差改正后得到一阶近似标准差要比不加偏差改正的小，而考虑泰勒级数展开的二阶项时，二阶近似要大于一阶近似标准差，在线性化过程中忽略高次项时可能会舍去某些信息，而考虑了部分随机量的随机性的方法在理论上更加严密。

4 结束语

非线性模型在线性近似过程中会带来模型误差，导致得到的最小二乘估计的参数估值是有偏的。本文考虑了Partial EIV模型参数估值的偏差并得到偏差改正后的参数估值，在方差分量估计中，参数估值对观测值改正数等有直接影响，进而影响方差分量估计的准确性。因此，本文将参数估计、偏差改正和方差分量估计作为整体进行迭代计算，将偏差改正后的参数估值代入方差分量估计中，从而获得更加可靠的方差分量估值与参数估值。根据不同的平差模型及数据结构，当系数矩阵误差与系数矩阵量级很大时，模型的非线性强度较低，参数估值的偏差必然很小，此时进行偏差改正得到的结果变化不大；当偏差较大时，进行偏差改正可以得到更好的结果；得到更加合理的方差分量估值对随机模型进行修正，从而获得更加合理的参数估值及精度信息，是对总体最小二乘理论的进一步完善。本文将偏差改正结合到方差分量估计中，然而并未对偏差量级对结果产生影响的程度进行分析，这也是今后将要开展的工作。