极大似然估计概念的微课程教学设计

陈永娟

(莆田学院 数学与金融学院，福建 莆田 351100)

0 引言

概率论与数理统计是一门基础课程，在高校中不仅是理工科各专业要学习它，管理类各专业、农、林、医、人文等专业也要学习它。但是由于它特有的一些思想方法，使得不少学生掌握起来比较困难。近年来很多概率统计教师，将微课应用于该课程的教学改革中，通常会通过一节十到二十分钟的微课讲清一个概念。如何进行教学设计把一个概念讲清讲透呢？本文给出一节极大似然估计的微课程教学设计，为概率统计微课程的教学设计起到一个抛砖引玉的作用。

1 教学背景

概率论与数理统计中，极大似然估计法的概念方法是在学生已经学习了点估计、矩法估计等概念之后学习的知识点。它是概率论与数理统计的重要概念之一。极大似然估计法应用非常广泛，在以往的教学中发现学生往往只会套模式做相关练习，而对极大似然估计的基本思想和估计参数的原则理解不透彻。一个很重要的原因是教师对这个方法的统计思想阐述得不够透彻。下面通过一节十多分钟的微课程教学设计，让学生能进一步理解极大似然估计的基本思想和概念。

2 教学方法和过程

根据思维习惯由直观到抽象的特点，首先给出一个简单的例子先让学生从直观上去估计参数，这样对于接下来较抽象的理论有较好的引导作用。

例1 一个盒子中装有若干个白色和黄色的乒乓球，不同颜色球的数量比为3:1，但不知哪种颜色的球比较多。现从中有放回地抽取两球,发现都是白球，试估计白球所占的比例。

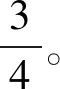
通过上面的简单例子，引入极大似然估计的基本思想：在一次随机试验中，如果有若干个可能的结果A，B，C，…。若在一次试验中，结果A发生了，则一般认为试验条件对A发生有利，基于此所做出的估计要使得A发生的概率最大[1]。

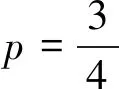
接着介绍极大似然估计法的来历，调动学生的学习兴趣。极大似然估计法，最早由高斯(C.F.Gauss)提出。后来由费歇(R.A.Fisher)1912年在《统计估计理论》一文中重新提出，并证明了此方法的一些性质。极大似然估计法这一名称也是他给出的[2]。

现在在前面直观理解的基础上严格阐述极大似然估计法。

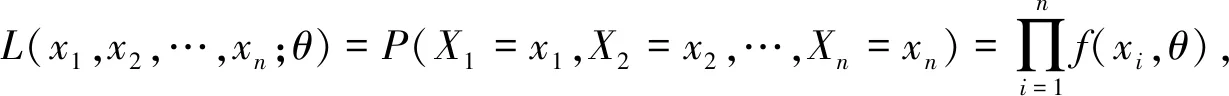
对抽象的极大似然估计法的几点说明：

(1)这里的θ有可能是一个参数，比如说泊松分布θ=λ；也有可能是向量，比如说正态分布θ=(μ,σ2)

(2)这里讲的似然函数就是联合概率函数，我们这里是以离散型随机变量为例，f(x,θ)就是X的分布律；若X是连续型随机变量的话，f(x,θ)就是X的密度函数。选择的参数要使得似然函数最大，也就是使得样本观测值出现的概率最大。由此得出极大似然估计法的原则：对每一组样本观测值，估计出的参数要使得出现样本观测值的概率最大。这是对极大似然估计最朴素和直观的阐述。

(3)极大似然估计法是从观测值出发的，因此直接求出的是极大似然估计值，要求估计量的话，注意把xi改为Xi。

(4)极大似然估计简记为MLE(Maximum Likelihood Estimation)，似然是对Likelihood的一种较为贴近的翻译，可以理解为可能性、看起来像的意思[4]。

下面，再通过一道跟上面的例题有密切联系的例题进行练习，让学生进一步理解极大似然估计法估计参数的原则以及解题步骤。

例2 一个盒子中装有若干个白色和黄色的乒乓球，不同颜色球的数量比为3:1，但不知哪种颜色的球比较多。现从中有放回地抽取3个球,发现取到的第一个球是白球，后面两个球是黄球，试用极大似然估计法估计白球所占的比例。

分析：在例1中学生只要通过直观就可以给出估计，这道题目难度稍微加深，考查如何根据极大似然估计的方法给出严格的估计。

解：根据极大似然估计法的定义，首先写出总体的分布：

X={1,取到白球

0，取到黄球

则概率函数

f(x,p)=px(1-p)1-x,x=0,1

写出似然函数,并带入样本观测值得：

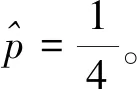
这个例题的设计非常关键，由例1学生能够直观理解的例题进行拓展，由浅入深地阐述极大似然估计的概念同时给出解题的步骤，同时融入了极大似然估计的基本统计思想。通过两个简单的例题就可以讲清极大似然估计的概念。

下面举一个比较贴近生活的应用例子。

例3[5]设电话总机在一天内接到的呼叫次数X服从参数为λ泊松分布P(λ)，现有42个数据如下：

呼叫次数012345>5出现的频数710128320

求参数λ的极大似然估计。

解：x1,x2,…,xn是来自总体X的一组样本观测值，则似然函数为：

两边关于λ取对数求导得似然方程为：

解得λ的极大似然估计值为：

根据题目给的样本数据求得

求得λ的极大似然估计值为1.905。

在传统的教学设计中通常只要求泊松分布参数的极大似然估计量，而没结合实际例子的具体数据，学生往往都只会依葫芦画瓢去进行计算。

通过这道例题既可以总结出极大似然估计解题的基本步骤：(1)根据样本构造似然函数；(2)对似然函数取对数求导得到似然方程；(3)解似然方程，求出参数的极大似然估计值；(4)写出参数的极大似然估计量。我们根据具体实例可以讨论具体的极大似然估计值怎么求。在选择案例的时候要看是否能说明问题，而不是越复杂越好。可以在传统的教学设计的例子中，根据学生的思维特点和学习中存在的困难进行适当的改编以得到合适的例子。

3 结束语

学生在应用概率统计方法的时候，常常都是生搬硬套，并不能真正理解它们的基本思想和原理，因此也就不能灵活应用。教师在教学过程中要讲透那些学生不易理解的概念。教师自己先要吃透相关的概念和思想。在微课程教学设计过程中，就一个点展开，要注意由浅入深，注重学生统计思想的建立，这样才能让学生真正掌握相关的概念。