一种递进关系规划模型在高温防护服中的应用

姚合军，杨 恒，崔金锦，焦筱然

(安阳师范学院 数学与统计学院，河南 安阳 455000)

0 引言

建立规划模型是设计高温防护服的一个主要方向，热量的传递过程中，通过一维抛物型偏微分方程来进行热量和温度之间的转换[1]。一般来讲，通过有限差分法对一维抛物型偏微分方程进行求解，具有高精度的特征[2]。传热方式一般为非稳态的，并且有热传递、热辐射和热传导三种传热方式[3]。人体的各个部位的热量是不同的，在这种情况下运用有限差分法对其求解，难免会因其运算量大、运算过程复杂造成困难。将人体模型进行适当简化，将其视为一个圆柱形模型，改进求解方法，增强模型的实用性[4]。人体在作业时，必然有着时间限制，即使身穿热防护服也仅有几秒的安全时间，故空气层和织物的厚度大小对防护性能的影响十分显著，因此关注温度的变化是必不可少的[5]。

然而，高温防护服领域的研究虽然取得了一定的进展[6]，但因其模型建立和计算的复杂性，在设计常用防护服时会受到一定的制约。本文基于傅立叶导热定律，根据一般防护服的性能要求对其边界条件进行了适当的放宽[7]。而且本文建立的规划模型，考虑了层与层之间的联系，分析了各层之间的数学联系，使模型计算更加准确，与实际效果更为吻合。

1 问题描述

⑴

由于热能密度在非常短的距离内可看作是恒定的，故可用Δx表示热量传递方向上的位置差，S表示圆柱体的横截面积，用体积与热能密度的积Q=qV=qΔxS表示热能。由热能守恒和偏微分的定义可以得到：

⑵

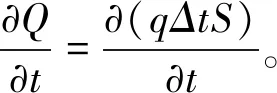
⑶

结合对热能守恒转化过的式子与傅立叶定律，可得到一维的偏微分方程：

⑷

此外，为了减少最终计算结果对实际问题造成的误差，我们引入了显热容这一概念[8]，即用Ci表示第i层的显热容，ρi是第i层材料的密度，ci是对应第i层材料的比热，从而有Ci=ρiCi(i=1,2,3,4)。由于ri和ci是常数，所以Ci也是常数。

2 模型建立

高温作业服装共有四层，其中前三层是由不同的材料组成，第IV层为空气层。基于本文上述假设，后面三层以及隔离层可以近似看作只存在热传导[9]。

2.1 专用服装的热传递模型

⑸

⑹

⑺

2.2 空气层的热传递模型

根据题中假设，可以得出空气层的热传递模型为：

⑻

其中，Ci(i=1,2,3,4)分别是I、II、III和IV层的显热容；ki(i=1,2,3,4)分别是I、II、III和IV层的热传导率；Ωj表示关于x的取值范围，其中Ω1=(0,L1),Ω2=(L1,L1+L2),Ω3=(L1+L2,L4),L4=L1+L2+L3,Ω4=(L4,L5),L5为人体皮肤，t是暴露在外部环境中的时间。q为人体自身的热源，人体自身温度和第I层防护服的外层温度约定为37℃，则q对x的偏导为0，外部环境温度约定为80℃。令mi表示ki与Ci的比值，由于ki(i=1,2,3,4)为热传导率，Ci(i=1,2,3,4)为定值，所以mi为确定值。由于空气层厚度较小，可以将其看成一个圆柱形封闭腔，忽略空气中传导和织物辐射作用[10]。

3 主要结果

根据题中所给的防护服的相关数据，层与层之间的距离较小，并且是一个封闭的环境，因此，在传热过程中，热量从外部传递到第I层末端时的温度和第II层的起始温度相同。即上一层末端的温度和下一层初始端的温度相同。对上述所给的服装热传递模型进行积分可以得到以下方程：

⑼

⑽

⑾

⑿

由于第I层末端时的温度和第II层的起始温度相同，即上一层末端的温度和下一层初始端的温度相同。即可得：T1=T2=T3=T4。即：

⒀

⒁

⒂

由于上一层的末端温度与初始层的初始温度相等，即T0=T1=T2=T3。对以上模型进行求解得：

c12=(c21-c11)x+c22

⒃

c22=(c31-c21)x+c32

⒄

c32=(c41-c31)x+c42

⒅

由上述参数之间的关系，可得出温度变化方程为：

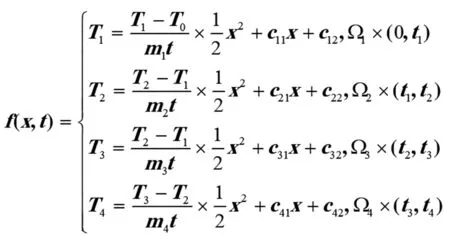
(19)

4 仿真算例

假设各层的密度、比热、热传导率和厚度如表1所示。

表1 各层的密度、比热、热传导率和厚度

其中，密度和比热为固定值，因此Ci=ρici,(i=1,2,3,4)为定值。

各分层温度随时间变化趋势。通过所建立的傅里叶模型将温度转换成热量，根据热传导公式，联立方程，利用差分法[4]，通过软件进行编程仿真，运行得出其温度分布如下表所示。

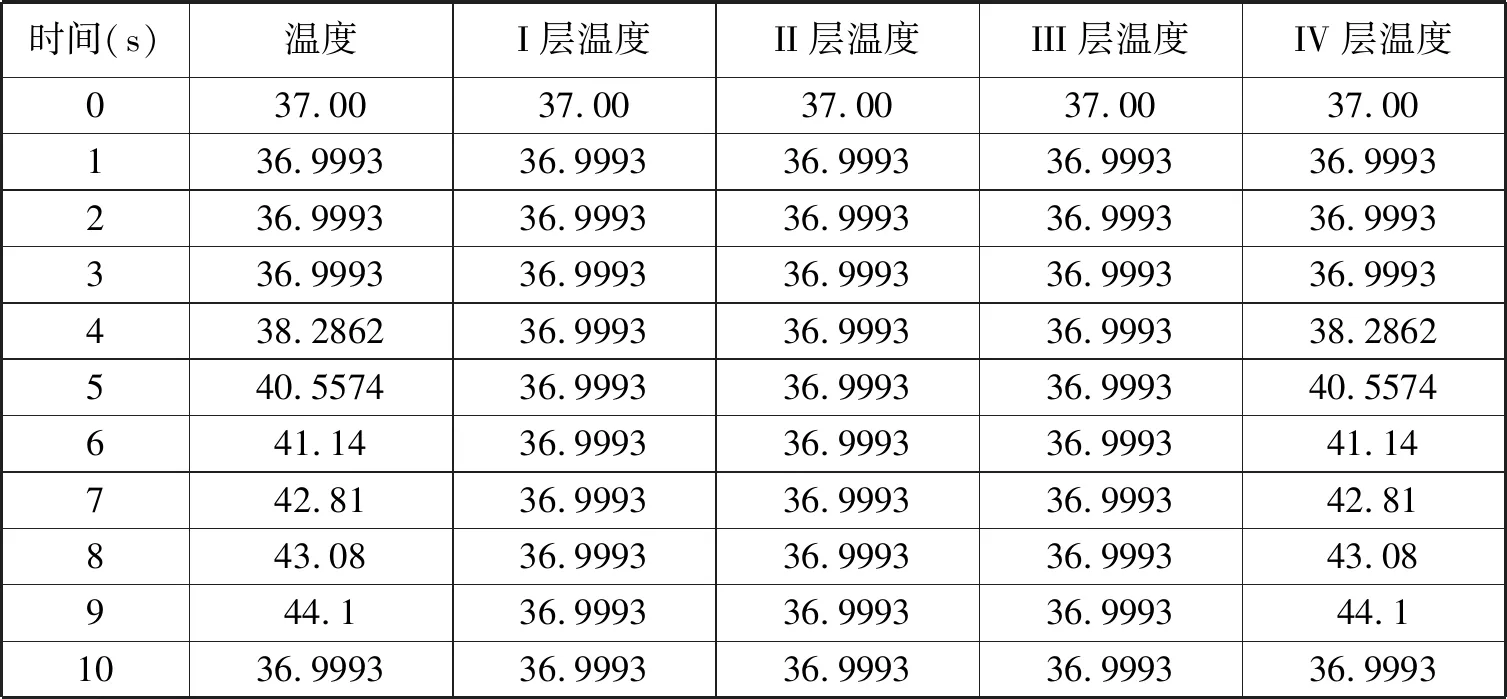
表2 各分层温度随时间变化趋势表

5 结论

根据所建立的模型，在外部热源通过防护服向人体传递热量时，每一层的交界处温度相等，即上一层末端的温度和下一层初始端的温度相等，因此整个传热过程具有连续性。本文在建立规划模型时主要考虑了层与层之间的联系，将规划模型有机地看做一个整体，使模型更加符合实际。而且模型具有适用性广、计算方法简便的优点。