一类五阶色散波方程解的平均性质

王宏伟,袁 伟,柴亚喃,韩校涛

(安阳师范学院 数学与统计学院，河南 安阳 455000)

0 引言

在研究具有弱横向效应的色散长波传播问题时,Kadomtsev和Petviashvili[1]提出了如下的KP方程

它是KdV方程在2维空间中的推广。如果研究的长波具有高阶色散项,就得到如下一类五阶色散波方程

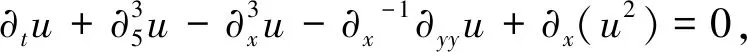
u(x,y,0)=ψ(x,y)

(1)

方程(1)适定性问题的研究,得到了许多学者的关注,取得了丰富的成果[2-5]。本文将研究方程(1)的解具有的积分平均性质,得到的主要结论如下:

定理1如果ψ∈L1(R2)∩H2,0(R2),u(x,y,t)是方程(1)的一个广义解并且u∈C([0,T];H2,0(R2)),那么对任意的t∈(0,T],y∈R在广义Riemann 积分的意义下,有

(2)

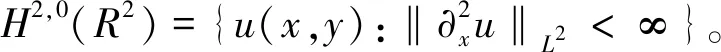
1 线性方程

首先考虑方程(1)对应的线性方程

u(x,y,0)=ψ(x,y)

(3)

它的解u(x,y,t)可以表示为

u(x,y,t)=S(t)ψ=G(x,y,t)*ψ,

G(x,y,t)=F-1(eit(ξ5+ξ3+η2/ξ))

下面我们证明线性方程的解具有积分平均性质。

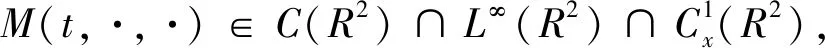
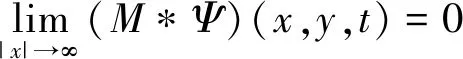
(4)

即,线性方程(3)的解u(x,y,t)满足如下的积分平均性质

证明:做变量替换η'=ηt1/2/|ξ|1/2,得到

G(x,y,t)

定义

下面证明，固定t>0,则H(λ)是连续的。当λ>9t/20时,相函数φ(ξ)=i(tξ5+tξ3+λ)没有驻点。当λ≤9t/20时,相函数最多有两个驻点ξ1,ξ2(ξ1<ξ2)。这里仅考虑最差的有两个驻点的情况。对充分小的ε>0,记

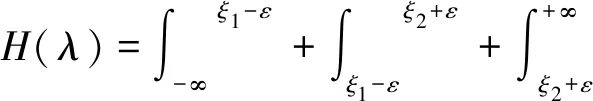
+I2(λ)+I3(λ)

易知I2(λ)是一个连续函数,又

故I3(λ)也是连续函数。同理,I1(λ)是连续函数。这说明G(x,y,t)是eit(ξ5+ξ3+η2/ξ)的傅里叶逆变换。

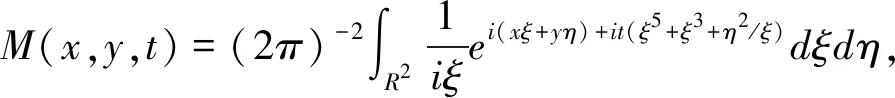
M(x,y,t)

令

下面证明N(λ)是连续函数,并且当|λ|→∞时,N(λ)→0

将N(λ)改写为

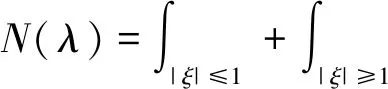
因为|ξ|-1/2在零附近是可积的,根据Riemann-Lebesgue定理知,N1(λ)是连续的,且

下面分两种情况讨论N2(λ)

情形1λ>9t/20

利用分部积分,有

第一项是连续函数,并且当λ→∞时极限为零.注意到

再根据控制收敛定理知N2(λ)是连续的,另一方面,当λ≥1时,有

故当λ→∞时,N2(λ)→0

情形2λ≤9t/20

在由N2(λ)定义的积分中,仅考虑积分区间为[1,+∞]的情况,(-∞,-1]的情况同理可得。此时,相函数φ(ξ)=i(tξ5+tξ3+λ)至多有一个驻点ξ0。此时,取充分小的正数δ,并记

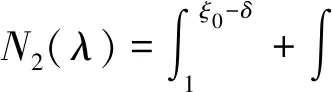
+I2(λ)+I3(λ)

最后,易知在广义函数意义下∂xM=G。因为M和G都是连续的,M关于变量x的古典导数就是G，定理得到证明。

2 非线性方程

利用线性问题的方法,并适当加强初值条件,就能证明本文的主要结论。

定理1的证明。根据Duhamel公式,方程(1)等价于下列积分方程

其中

使用定理2中的记号,有

M(x-x',y-y',t-s)

令

则利用Lebesgue微分定理,有

由于L在[0,t]上关于变量s是可积的,由Lebesgue定理知：

是一个C1函数,并且

最后来证明(2)。根据线性问题的证明知,固定s,x',y',当|x|→∞时,上式积分号中的函数趋于0.另一方面,由于

|M(x-x',y-y',t-s)(uux)(x',y',s)|

根据u∈C([0,T];H2,0(R2)),上式右端关于变量s,x',y'可积并且不依赖于x.由控制收敛定理知(2)成立.定理得到证明。