区块链系统中矿池间的博弈问题及优化*
杨 天,薛 质
(上海交通大学 电子信息与电气工程学院,上海 200240)
0 引 言
区块链是一种分布式共享总账,系统中的每一个参与者都负责数据的记录与存储,从而实现了去中心化[1]。目前在各种区块链系统中,比特币是区块链最成功的应用之一,它在区块的生成过程中使用了PoW(Proof of Work,工作量证明)机制。PoW是一种激励性算法,它的核心概念是通过矿工之间的竞争来保证数据的安全性、连续性与一致性。系统中各节点根据各自的算力争相角逐,共同解决一个求解复杂但是验证容易的SHA256数学问题[2]。其中解决该问题的节点会提供一个合理的Block Hash,同时获得在区块中记录数据的权利,并得到系统自动生成的比特币奖励。一个符合要求的Block Hash由N个前导零构成,零的个数取决于网络的难度值。要得到合理的Block Hash需要经过大量尝试计算,计算时间取决于机器的哈希运算速度。当某个节点提供出一个合理的Block Hash值,说明该节点确实经过了大量的尝试计算,当然,并不能得出计算次数的绝对值,因为寻找合理Hash是一个概率事件。可见在PoW机制下,每个矿工为了获得比特币奖励将会尽其所能地利用其算力解决问题并尝试挖矿,新的数据区块不断生成,从而产生了区块链[3]。
其它基于PoW的区块链系统也是以同样的方式运作的,虽然各种系统所提出的数学难题并不相同,但是都有一个共同特征:用算力换收益,并且利用分布网络节点的工作量证明使各个节点达成共识,从而实现交易数据的记录与存储,同时产生了一套有时间先后顺序的,不可篡改的,可信任的数据库。通过复杂的校验机制,区块链系统可以保证数据库中数据的完整性,连续性,和一致性。即使部分参与者作假也无法改变区块链的完整性,也无法篡改区块链中的数据。简而言之,区块链技术涉及的关键点有:去中心化、集体维护、去信任、可靠数据库、时间戳、非对称加密等[4]。
1 背景知识
1.1 矿池概念
区块链系统中,生成区块的过程被称为挖矿,所有参与挖矿的节点被称为矿工。由于全网算力非常巨大,而区块产出有限,单个设备或少量的算力都很难在比特币网络上获取到比特币网络提供的区块奖励。为追求稳定收益,人们自发地将算力联合起来形成矿池。一个矿池有一位管理员,当矿池的一位参与者挖到区块时,比特币奖励会发送到矿池管理员。然后,管理员根据每个参与者对矿池算力的贡献,向参与者发放比特币奖励。在此机制中,不论个人矿工所能使用的运算力多寡,只要是通过加入矿池来参与挖矿活动,无论是否有成功挖掘出有效资料块,皆可经由对矿池的贡献来获得少量比特币奖励,亦即多人合作挖矿,获得的比特币奖励也由多人依照贡献度分享。
1.2 区块截留攻击
由于每一个矿工只要提供一个网络ID数字就可以加入矿池,一个开放的矿池很容易遭受攻击。具体形式为:一些矿工会发送部分工作量证明(Partial Proof of Work,对产出几乎无帮助,只是证明干了活),抛弃完整工作量证明(Full Proofs of Work,收益来源)。这就是所谓的区块截留攻击,这个行为看似损人不利己,那么选择攻击的矿工的目的是什么呢?主要原因是,区块链协议具有难度自适应的特征,会根据当前区块生成速度调整前导0的个数,从而改变难度,控制区块生成速度保持不变。有矿工选择攻击会导致矿池有效算力减少,协议为了保持区块生成速度不变,自会降低挖矿难度,这样滥竽充数的矿工就会得到更多收益。其次是因为,得到奖励的矿池会根据工作量证明按照矿池中每个矿工贡献算力的比例将所获奖励分配给每一个矿工。而完整的工作量证明很难生成,偷奸耍滑的矿工可以选择向开放矿池发送部分工作量证明来获得本该贡献实际算力才能得到的奖励。
在一个开放矿池中,一个矿工可以选择与其他矿工合作或是对其他矿工发动区块截留攻击,两种选择都会获得相应的收益。当所有矿工都选择攻击时,它们获得的收益比所有矿工都不选择攻击时获得的收益要小。这种情况被称为PoW共识算法中的挖矿困境[5],对于一个矿工来说攻击是最好的选择,而这个选择会使系统收益减少。所以,为了促使矿池中的所有矿工合作挖矿提高系统收益,需要开发一种激励性机制来促进矿工合作从而优化区块链PoW共识算法。
1.3 初步建模及策略
为了避免区块链中的矿工陷入挖矿困境,选择合作的矿工可以采取一些策略来解决攻击矿工“拿钱不干事”的问题或者尽量减小损失。有了相应的策略,矿池中一个矿工不管与它竞争的对手矿工采取什么策略,它都能单方面地控制对手从自己这里得到的期望收益并分给对手一定比例的期望收益从而促进对手更倾向于合作。以更宏观的视角分析,不妨尝试将两个矿工之间的博弈以类似的思路放大为两个矿池间的博弈。考虑到全网的其中两个矿池A和矿池B,B矿池派出总算力为b的矿工,在A矿池注册,这些矿工在A矿池进行区块截留攻击。这样一来总算力降低,根据协议,区块生成难度降低,B矿池获得正收益,而A矿池通过不断减少的收益中能发现它正在遭受攻击,但很难发现究竟是那些矿工进行攻击。实际情况中,攻击往往是双向的,设A矿池派出的渗透算力为a,B矿池的渗透算力为,则对于A矿池来说,面对B矿池可以采取多种策略来应对。
目前常见的策略有如下9种[6](分别用Pn表示):
P1--ALLC:All Cooperate,永远合作策略,无论对手采取何种策略,都选择合作,即令渗透算力a恒为0。
P2--ALLD:All Defect,永远背叛策略,无论对手采取何种策略,都选择背叛,即令渗透算力a恒为最大。
P3--TFT:Tit For Tat,一报还一报策略,第一次选择合作(即a=0)此后,如果对手的渗透算力b大于某一阈值,则下一轮背叛(即a=max),否则合作(即a=0)。
P4--Grim:冷酷策略,第一次选择合作(即a=0),只要对手背叛一次,就不再合作,令a=max。
P5--WSFS:Win Stay Fail Shift,赢存输变策略,第一次选择合作(即a=0),之后每一轮如果收益高于某一阈值,就保持策略不变,否则采取相反的策略(即a=max)。
P6--Random:离散型随机取值策略,a以等概率取0或max。
P7--TFT_D:TFT_Defect,类似于TFT,区别在于第一次选择背叛(即a=max)。
P8--Grim_D:Grim_Defect,同上,类似于Grim。
P9--WSFS_D:WSFS_Defect,同上,类似于WSFS。
2 矿池博弈模型与IPD
2.1 数学建模
根据1.3所描述的情况,全网中的两个矿池A和B互相派出渗透矿工攻击对方。为方便计算,设全网总算力为1,A矿池算力为s,B矿池算力为t,显然s+t<1。A矿池派出的渗透算力为a,B矿池的渗透算力为b,派出的间谍矿工将进行区块截留攻击,因此不贡献任何算力。能派出的算力有限,故可设0≤a≤0.1s。全网实际算力从1降低为1-ab,故单位算力的产出速度提升到原来的倍。
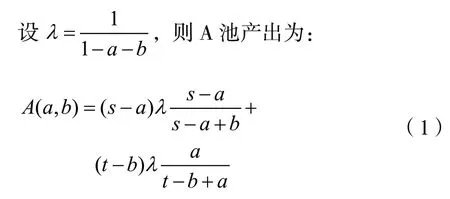
同理,B池产出为:
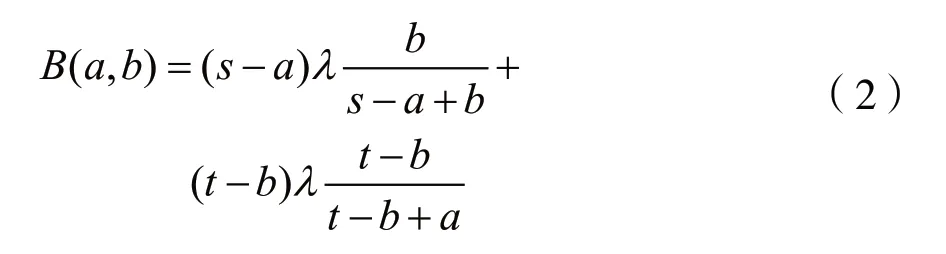
由于0≤a≤0.1s,0≤b≤0.1t,s与t的值相差不大,故可将a、b视为小量,则a2、b2、ab趋近于0。所以等式(1)可以化简为:
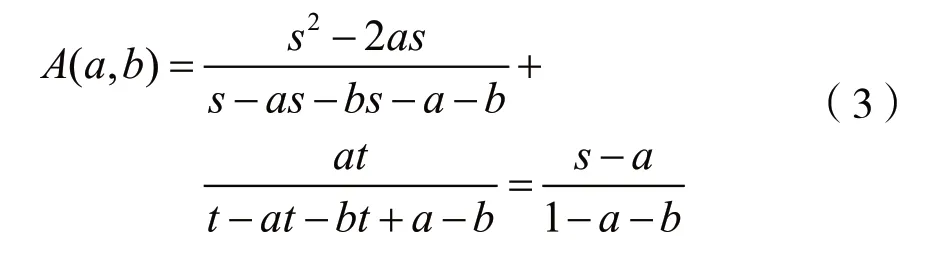
同理:

设s=0.2,t=0.2,b=0,A(a,0)的图像如图1所示。

图1 矿池B选择合作时,A矿池收益与渗透算力a的关系
这是近似线性的单调递增函数,即A矿池攻击越强(a↑),其收益越高(A(a,b)↑)。
将(3)与(4)相加得到A矿池与B矿池的总收益:

将a+b视作一个变量,则G(a,b)与a+b关系如图2所示。
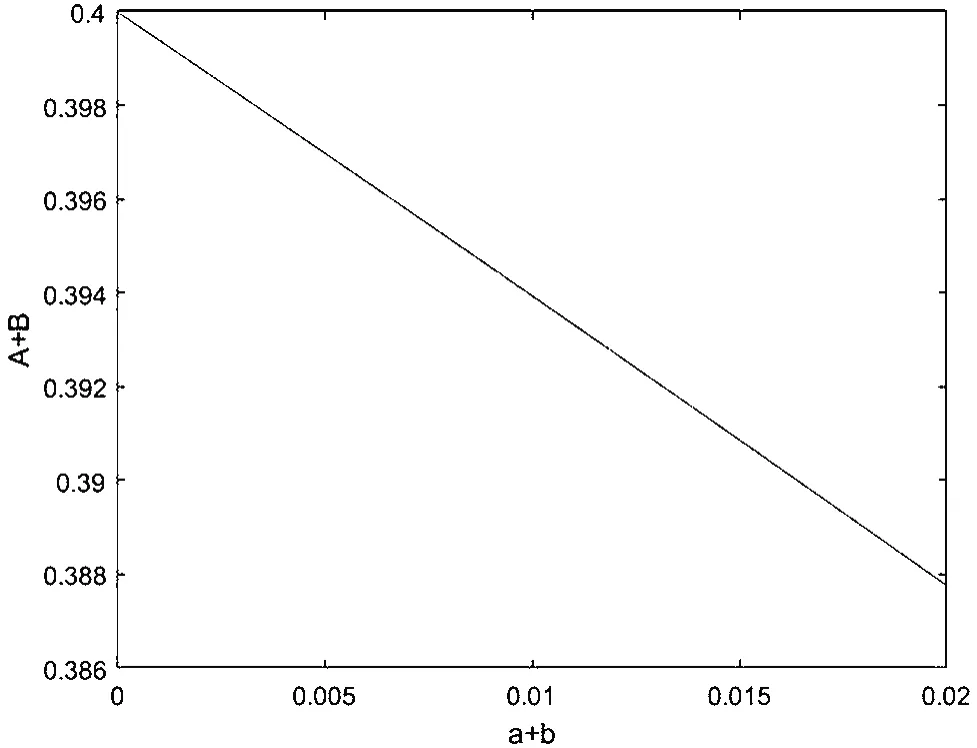
图2 A、B两矿池收益总和与渗透算力a、b之和的关系
这是近似线性的单调递减函数,即两者的攻击越强((a+b)↑),总收益越低(G(a,b)↓)。
2.2 囚徒困境与IPD
以上所述的特征与经典的囚徒困境十分相似。即两个共谋嫌疑犯被捕后单独审讯,如果两个人都不坦白罪行,则由于证据不足各判一年;如果其中一人坦白,另一人不坦白,则坦白的人因立功而立即获释,不坦白的人因不合作而被判十年;两个人都坦白罪行,则证据确凿,各判八年。由于囚徒无法信任对方,因此倾向于互相揭发,而不是同守沉默。最终导致纳什均衡仅落在非合作点上的博弈模型。其收益矩阵如表1所示。

表1 经典囚徒困境收益矩阵
这与挖矿困境的相同点在于,坦白(攻击)对个体而言是最优的选择,而对于总体(全网)而言,每个个体都选择坦白(攻击)就不是最优选择了。不同点在于,经典囚徒困境中策略集只有(坦白,沉默)两种取值,是一个离散问题;而矿池间的博弈问题中,策略集是渗透算力(a,b),是连续的 控制量。
囚徒困境指出,如果只进行一次博弈,那么双方都会毫无疑问地选择背叛(在矿池博弈中,即令a=0.1s,b=0.1t)。但在实际情况中,双方往往会进行多次,甚至海量的相互博弈,为此引入IPD(Iterated Prisoner's Dilemma,重复囚徒困境)模型。IPD中,博弈被反复地进行。因而每个参与者都有机会去“惩罚”另一个参与者前一回合的不合作行为。这时,合作可能会作为均衡的结果出现。欺骗的动机这时可能被受到惩罚的威胁所克服,从而可能导向一个较好的、合作的结果。作为反复接近无限的数量,纳什均衡趋向于帕累托最优(没有再进行帕累托优化的余地)[7]。
囚徒困境的主旨为,囚徒们虽然彼此合作,坚不吐实,可为全体带来最佳利益,但在无法沟通的情况下,因为出卖同伙可为自己带来利益,也因为同伙把自己招出来可为他带来利益,因此彼此出卖虽违反最佳共同利益,反而是自己最大利益所在。但实际上,执法机构不可能设立如此情境来诱使所有囚徒招供,因为囚徒们必须考虑刑期以外之因素(出卖同伙会受到报复),而无法完全以执法者所设立之利益(刑期)作考量。
同样的,对于两个矿池A和B在无限次重复博弈中,博弈者可以采用的策略有无穷多种,采用什么样的策略才可以实现相对更高的收益呢?收益较高的策略之间存在共性吗?Axelrod实验可以解决这个问题。
Axelrod实验是以计算机程序对弈、竞赛的方式进行的。他要求参与竞赛的编程者充当囚徒困境的局中人,以谋求博弈收益的长期最大化为目标,用计算机程序编成特定的策略,每一策略按一定的规则实施合作或者背叛来对付对手。然后用单循环赛的方式将有所参赛程序两两对弈。[6]显然,不同的策略对弈会有不同的得分结局,这样就可以通过比较每个策略得分的多少来衡量其优劣。
2.3 不定值策略与定值策略
第一节最后提到的九种策略正是经典Axelrod实验中的常见策略,在本文的矿池博弈问题中,策略集被连续化,取值并不确定,在此基础上设计出新的策略:
P10--不定值策略:a的取值在[0,max]区间内均匀分布。
在此基础上对不定值策略进行帕累托优化(在没有使任何矿池收益减少的情况下,至少使一个矿池的收益增加)。单次博弈不可能保证该优化的实现,因为若a=0,b=0,根据等式(5),总收益G(a,b)已达到最大值,则矿池A,B其中一个收益增加必然会导致另一个收益减少;同理,若a、b不全为0,说明至少有一个矿池在攻击对方,则无论是攻击矿池还是合作矿池收益增加后必然会导致对方收益减少。所以只有尽可能地在重复博弈中实现帕累托优化。在非合作关系中(a、b不全为0),纳什均衡状态即为帕累托最优,即总收益G(a,b)不变。为了接近最优状态,根据等式(5),a,b不全为0时,a在b不为0时取0;而在b再次为0时,设b从不为0到重新取0共经历了n+1轮,a此时取值为m,且满足本轮G(a,b)的n倍等于前n轮G(a,b)之和。这就是基于不定值策略的优化策略--定值策略:
P11--定值策略:第一次令a=0,若此后b一直取0,则a继续取0,若某一轮b>0,则a继续取0,设本轮b取值为b1,下一轮若b>0则a继续取0,b取值为b2,依此类推。在b>0之后的第n+1轮b再次为0,此时设a取值为m,且m满足:
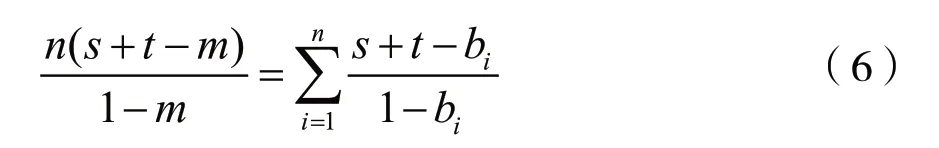
该策略理论上可以使两矿池接近纳什均衡,具体表现还要通过数值仿真来验证。
3 数值仿真
3.1 两两博弈的仿真结果
本文一共提出了11种不同的策略(经典策略9种,新设计策略2种),两两匹配,共有55次不同的博弈(每次模拟100轮),这里仅选取其中一些具有代表性的结果进行展示和分析。
计算可知,每轮博弈中,一方的最低收益为0.183 7,最高收益为0.204 1,差距仅10%左右,直接将收益作为纵轴作图,近似为线性,很不直观。为解决这个问题,可将每轮的收益减去0.183 7,称为“额外收益”,并以此为纵轴作图,使得结果较为直观。
部分结果如图3、图4、图5、图6所示。
图3表明,ALLC策略平均收益低于离散型随机取值策略。
图4、图5表明,当定值策略、ALLC、TFT、Grim、WSFS等友善型策略两两互相博弈时,会进行持续合作从而获得不错的收益(约1.6)。
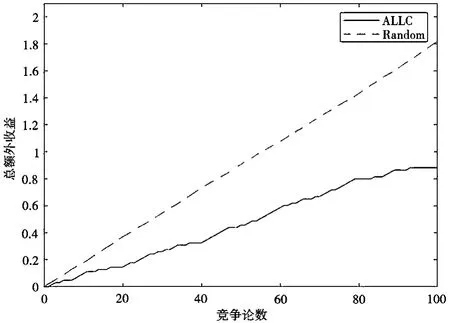
图3 P1与P6的竞争结果

图4 P1与P11的竞争结果
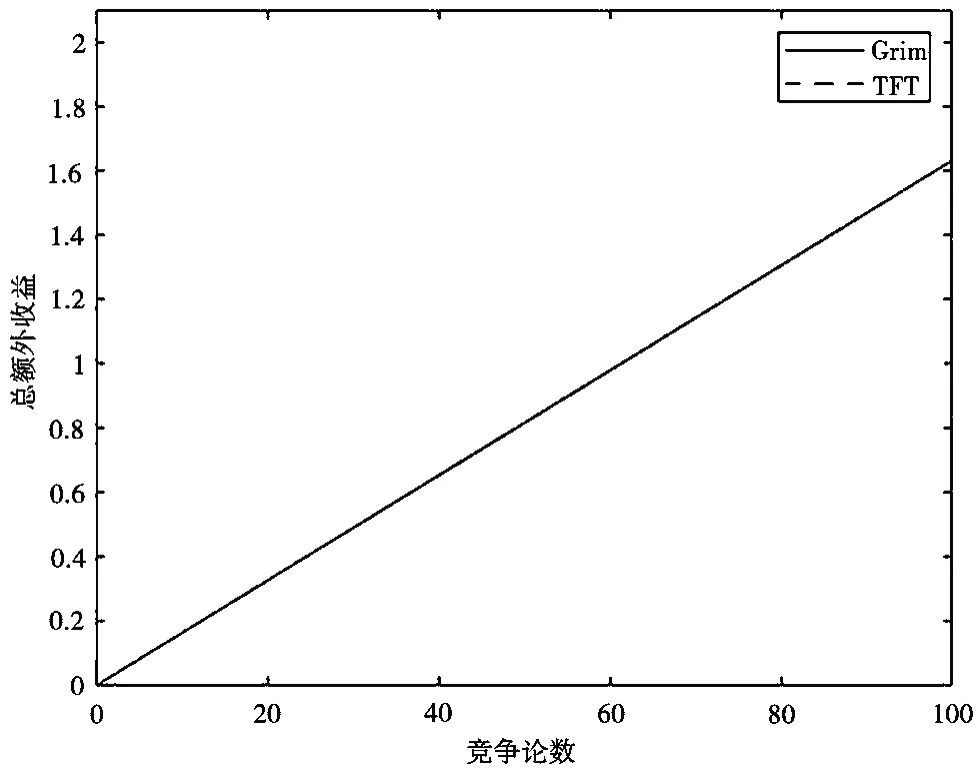
图5 P3与P4的竞争结果

图6 P10与P11的竞争结果
图6 表明,定值策略会根据对手策略做出相应的调整,导致不管和谁博弈,其收益都接近,除了ALLD。定值策略和ALLD的博弈与ALLC和ALLD的博弈是一样的。
3.2 总体表现的仿真结果
单看两两博弈的结果很难分析每一个策略的优劣,为此,我们统计了每个策略与其它所有策略进行博弈时的平均收益,并从高到低进行排序,结果如图7所示。
图7表明,表现最好的是定值策略,WSFS仅次于定值策略。表现最差的是TFT_D、Grim_D。
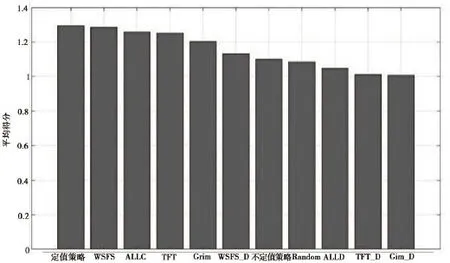
图7 11种策略的总体表现排名
3.3 仿真结果分析
对上述仿真结果进行分析,归纳出该博弈模型的以下特点:
(1)ALLD策略在每一次博弈中都不吃亏,但在总体上却是一种很差的策略;
(2)一般而言,“善意”的策略表现要优于“贪心”的策略;
(3)第一次的选择非常重要,对整个策略的表现影响很大。
传统IPD中,TFT策略和Grim策略表现最佳。而在该区块链博弈模型中,定值策略和WSFS策略表现最好,且定值策略较传统的WSFS更胜一筹。
4 总结与展望
矿池间的相互攻击是区块链中的常见现象,但此前的研究工作大多集中在单个矿池内矿工间的相互博弈。在本文中,我们首次对该问题进行了研究。
在研究方法上,我们选用了数学建模和数值仿真的方法,参考了经典的囚徒困境模型和IPD模型,但根据该问题的特点自行建立了具有连续性的收益矩阵,并根据该矩阵设计了两种新的策略——不定值策略、定值策略,并编写代码进行仿真。
在仿真中,我们比较了11种不同的策略,结果也与传统IPD模型有较大差异。根据结果,我们建议矿池的管理者采取定值策略或WSFS策略。
在矿池的博弈模型中一定存在更为优秀的策略等待我们去发掘,也有很多问题摆在我们面前。是否可以引入某些遗传算法,令目前设计的策略进行组合、突变或演化呢?超过两个矿池的多矿池博弈模型中,各种策略及其效果又会如何呢?后续工作将对这些情况进行研究和分析。

