两种高程坐标预测模型的精度对比分析

张明敏,刘 盼,周海龙,从建锋

(山东科技大学 测绘科学与工程学院，山东 青岛 266590)

目前，IGS测站在全球分布越来越多，积累近二十年的坐标时间序列，准确分析其变化特征，从而获得精确的测站坐标，不仅对于研究大陆板块运动具有重要的意义，而且可以对各种坐标参考框架进行修正，进一步提高IGS测站坐标的精度[1-2]。鉴于IGS测站的广泛性及重要性，对IGS站点坐标的准确预测不仅在气象预报，高精度快速测绘等领域具有重要作用，而且可以为地震分析预报、地壳变形监测、研究地球物理现象提供一定的参考信息。GPS坐标时间序列的研究始于上世纪九十年代，随后越来越多的学者通过研究GPS坐标时间序列获得更多测绘学相关方面的成果[3]。国内外学者研究发现GPS 坐标时间序列中存在明显的周期性(周年、半周年)运动，且在坐标垂向分量最为明显[4-5]。根据不同研究角度，相关学者对GPS 坐标时间序列时频分析提出诸多方法，如主成分空间滤波法、最大似然估计法、小波相干分析法及功率谱分析法等[6-9]。此外，在时间序列模型研究方面，传统时间序列模型存在建模过程复杂、无法动态调整模型参数、稳定性弱等缺陷[10]，因此，学者们又提出自回归综合移动平均模型、奇异普分析模型和基于BP神经网络的时间序列融合模型等改进模型[11-14]。为达到对站点高程精准预报及稳定性监测目的，选择高精度的时间序列模型至关重要。基于此，本文根据SOPAC提供的时间序列数据，分别确立多项式周期模型参数与自回归移动平均(Autoregressive and Moving Average，ARMA)模型参数，并对这两种模型的预测精度进行实验验证及对比分析，从而选出最优模型。

1 数据获取及预处理

1.1 数据来源

SOPAC提供IGS基准站单天解坐标时间序列数据产品，主要分为RAW-TRE、CL-TRE、CL-RES及CL-DETRE等不同类型，为了实验验证及对比分析两种模型的预测精度，在区域上，本文选取我国及周边7个IGS站CL-TRE产品(经数据分析中心对原始观测数据降噪后的坐标时间序列)的高程坐标。所选站点如图1所示。由于2014—2017年IGS站时间序列数据缺失严重，所以选用于拟合模型的时间序列范围为2009-01-01—2012-12-31，并对2013全年数据进行预测及精度检验。

图1 所选IGS站点分布

1.2 数据预处理

通过观察选取的GPS站点高程时间序列，发现时间序列观测值中包含少量的突变点和间断点。在对高程坐标时间序列进行周期特性分析时，都应剔除这些孤立值且将间断点数据补充完整，以免降低分析精度。本文采用稳健孤立值探测法IQR准则剔除突变点[16]，同时，利用正交多项式做最小二乘拟合完成间断点插值。数据预处理前后对比如图2所示，鉴于篇幅有限，文中列出4个测站预处理后高程坐标时间序列的对比图，其中突变点明显减少，间断点也得到有效处理。

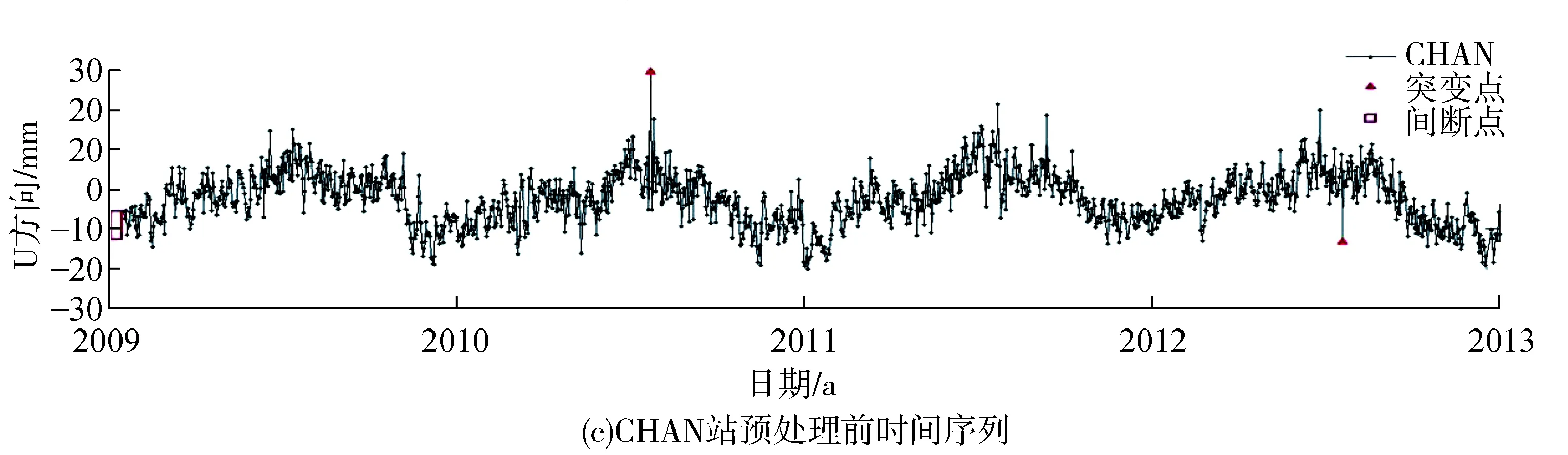
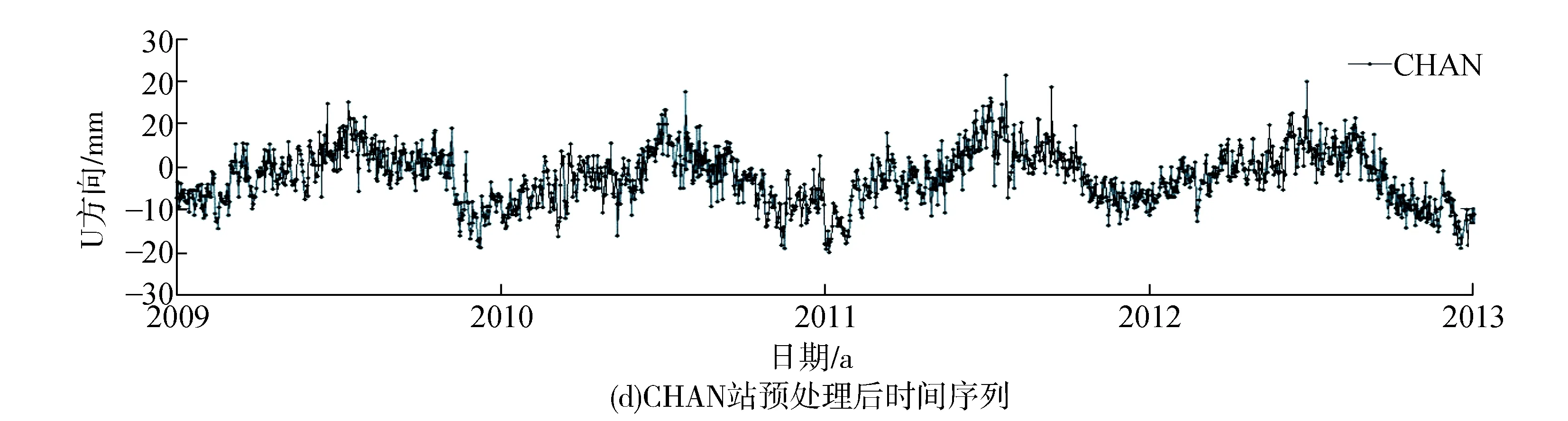
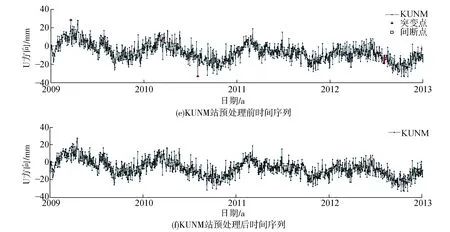
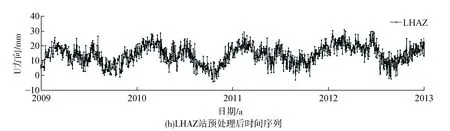
图2 各测站预处理前后时间序列对比

2 模型参数建立及数据测试分析

2.1 多项式周期模型

2.1.1 功率谱分析

功率谱分析是一种通过傅里叶变换将时域内的信号转换到频域内进行研究分析的方法，主要用来分析离散数据的周期特性。若一组离散数据具有周期性，则其周期运动对应的功率在全部功率中占很大比重，在功率谱图中对应着功率的峰值[14]，从而在时域内不易反映出的特性，可以在频域内很容易观察出来。

对IGS站点消除趋势项并进行傅里叶变换后，得到各个测站U分量的功率谱，见图3。通过观察各个测站高程方向坐标时间序列的功率谱图可以明显地看到时间序列周期特性趋于一致，除了具有明显的年周期项外，还有相对年周期能量较小的半年周期项。虽然不同站点的周期并非完全相同，即并不是严格意义上周年项周期为365.25 d，半周年项周期为182.62 d，但可从图3中看出3个测站的年周期在363～368 d内，半年周期在181～184 d内，即可以进行周期拟合。

2.1.2 模型构建

各站点高程方向坐标以年周期运动为主，同时存在半年周期运动。对于趋势项通常采用多项式函数进行拟合，而周期项可采用周期函数进行拟合，故本文采用的拟合函数模型为：

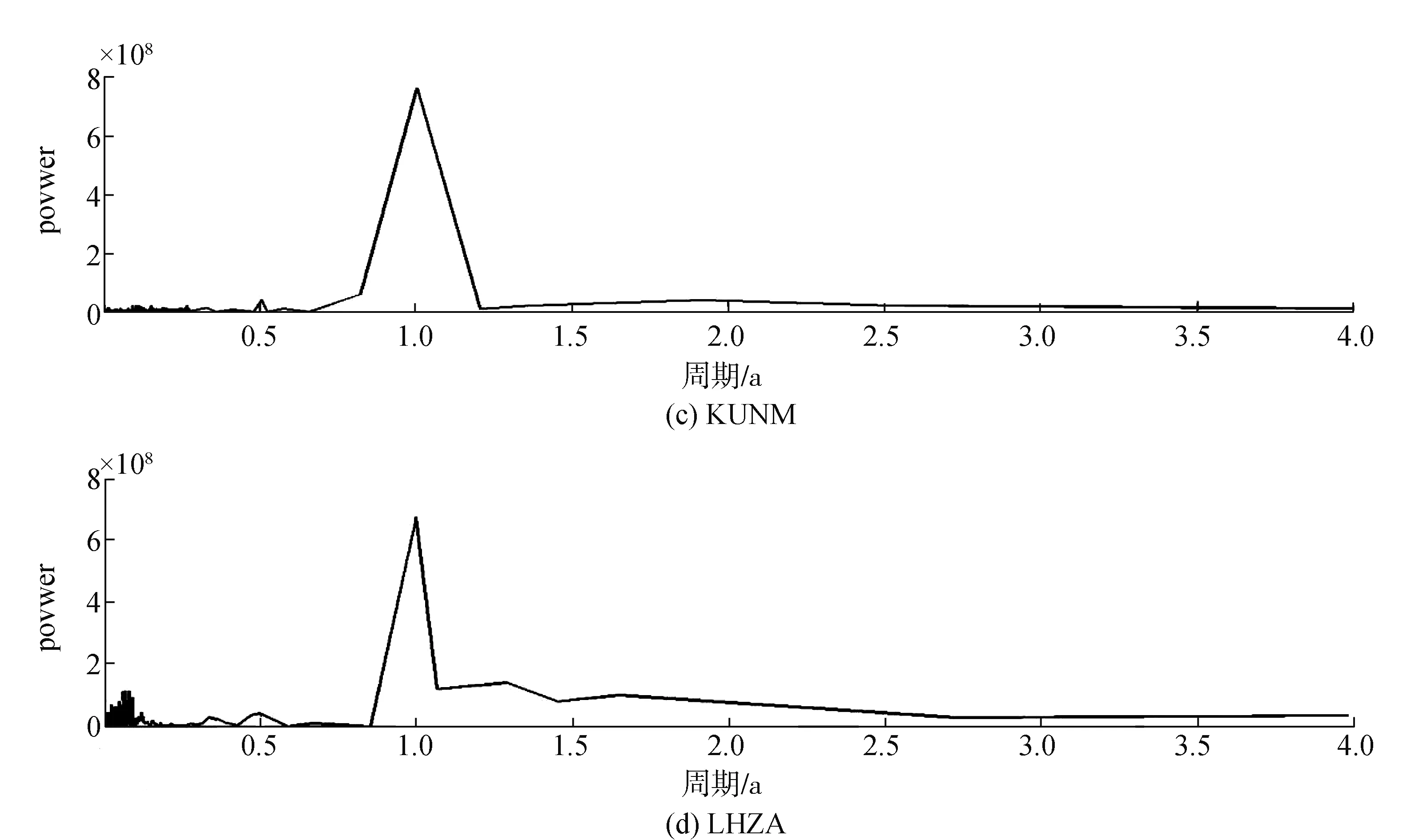
图3 4个IGS站高程方向上的功率谱

yi=a+b·ti+A1sin(2πti+φ1)+

A2sin(4πti+φ2).

(1)

式中：a为常数项，b为线性运动速率，A1，φ1分别为年周期项的振幅和相位，A2，φ2分别为半年周期项的振幅和相位。对式(1)线性化后变为：

yi=a+b·ti+csin(2πti)+dcos(2πti)+

esin(4πti)+fcos(4πti).

(2)

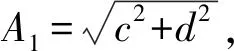
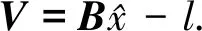
(3)

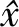
(4)

将2009-01-01—2012-12-31 IGS测站高程坐标代入上式，可求得各测站的拟合函数模型的参数，见表1。由表1可知每个站点的年周期项振幅比半年周期项振幅大，说明年周期运动是站点的主要运动规律。

表1 各测站拟合参数

2.2 ARMA模型

ARMA模型为

Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p-

θ1∈t-1-θ2∈t-2-…-θq∈t-q.

(5)

式中:p和q是模型的自回归阶数和移动平均阶数；φ，θ是不为零的待定系数；Xt是平稳、正态、零均值的时间序列；∈t是独立的误差项。建模的基本步骤：①消除IGS站点高程坐标时间序列的趋势项；②采用AIC准则确定p，q阶数的值；③利用Matlab软件确定模型参数，同时，查看残差∈t是否为白噪声序列判断模型的适用性；④增加模型趋势项。

2.3 模型验证及对比分析

利用以上两种模型分别预报所选测站2013-01-01—2013-12-31的高程坐标，并与SOPAC提供的时间序列数据进行对比分析。预报结果如表2所示。

表2 两种预测模型的预报中误差对比

由表2可知，多项式周期模型的预报中误差绝对值在2～4.5 mm之内，其平均值为±3.63 mm，预报中误差绝对值的最大值为4.10 mm，最小值为2.93 mm，其中，只有BJFS站的预报中误差绝对值小于3 mm，而CHAN站与KUNM站的预报中误差绝对值则大于4 mm。在ARMA模型中，预报中误差绝对值均小于4 mm，平均值为±3.33 mm，此外，该模型预报中误差绝对值的最大值为3.75 mm，最小值为2.71 mm，除BJFS站的预报中误差绝对值小于3 mm外，LHAZ站的预报中误差绝对值同样小于3 mm。通过对比两种模型的预报中误差，发现ARMA模型的预报精度整体高于多项式周期模型，且精度提升在5%以上，其中，BJFS站、CHAN站及LHAZ站的精度提升在6%～7%之间。KUNM站与SHAO站的精度提升甚至高于10%，这可能是由于预处理前的KUNM站与SHAO站时间序列完整性强所造成的，同时，在多项式周期模型中，所选IGS测站预报中误差的标准差为0.51 mm，而在ARMA模型中，所选IGS测站预报中误差的标准差为0.33 mm，可见，ARMA模型的稳定性强于多项式周期模型。综上可知ARMA模型更加适合预报测站高程坐标。

3 结束语

本文通过对多项式周期模型与ARMA模型进行实验验证及对比分析。发现两种模型的坐标预报中误差绝对值均在4.5 mm以内，即符合预报精度，同时，ARMA模型的预报精度较多项式周期模型的预报精度提升5%以上，且稳定性高于多项式周期模型，由此可见ARMA模型更加适合作为站点高程预报模型。本文用7个IGS站4年的数据拟合各测站高程方向的时间序列模型，有待用更长的时间序列和更加精确的模型加以检验及水平方向的分析。