高考数学临场解题策略之线性规划

田 保

(安徽省铜陵市第一中学 244000)

《普通高中课程标准》中说明：线性规划是利用数学为工具，来研究一定的人，财，物，时，空等资源在一定条件下，如何精打细算巧安排，用最少的资源，取得最大的经济效益，它是数学规划中理论较完整，方法较成熟，应用较广泛的一个分支，并能解决科学研究，工程设计，经济管理等许多方面的实际问题.

一、线性规划在历年考试的比重

从近几年的高考试题看，高考中常常以选择题、填空题的形式考查二元一次不等式组表示的平面区域的图形形状以及目标函数的最大值或最小值，有时也在解答题中考查线性规划.求函数的最优解等问题是高考的一种考查方向.

二、线性规划之常规思路解法

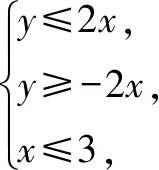
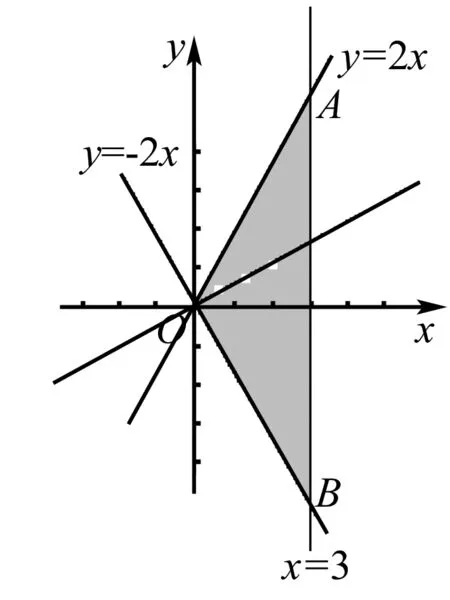
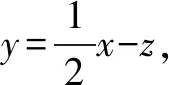
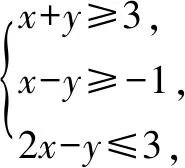
A.6 B.7 C.8 D.23

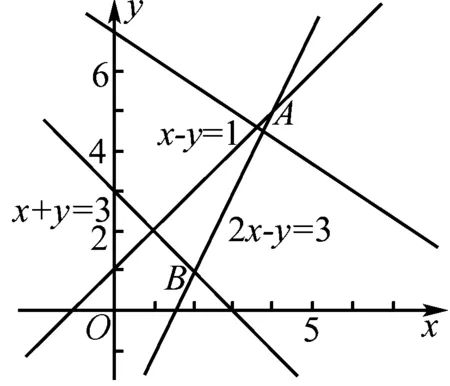
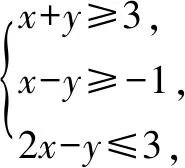
解题回顾求解步骤：(1) 画可行域——画出线性约束条件所确定的平面区域；

(2) 过原点作目标函数直线的平行直线l0；

(3) 平移直线l0，观察确定可行域内最优解的位置；

(4) 求最值——解有关方程组求出最优解，将最优解代入目标函数求最值.

三、临场解题方法

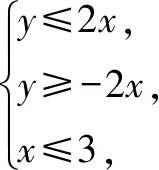
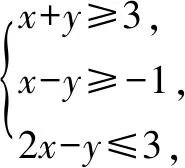
但有时此种方法也会失效，如：

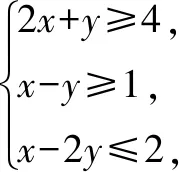
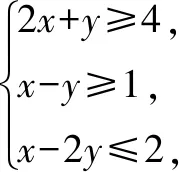
而我们用常规思路画线性规划图解答如下：

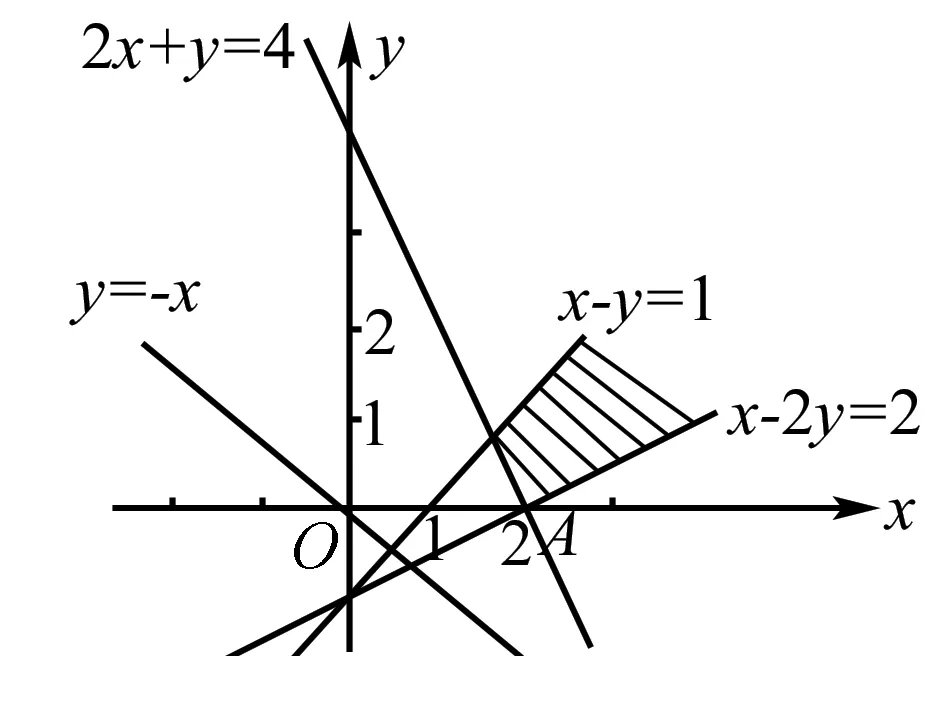
解析画出不等式表示的平面区域，如右图，由z=x+y，得y=-x+z，令z=0，画出y=-x的图象，当它的平行线经过A(2,0)时，z取得最小值，最小值为z=2.

为什么出现两种不同的

此法总结：1.找出可行域的交点；

2.把交点代入目标函数；

3.比较大小，(如求最小值)那么就取最小的那个值；

4.把取最小值的那个点代入到约束条件中检验，看是否满足其条件，不满足，取较小的那个值，再检验，依次下去.

四、缺点和不足

近几年不少地区考查了线性规划的逆向性问题，已知目标函数的最值，求约束条件或目标函数中参数的取值问题，对这类问题的求解只能根据约束条件画出可行性区域的方法求解.