一道解几题的解法探究

李丁琪

(河北省正中实验中学 050800)

一、例题

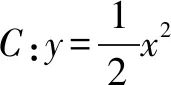
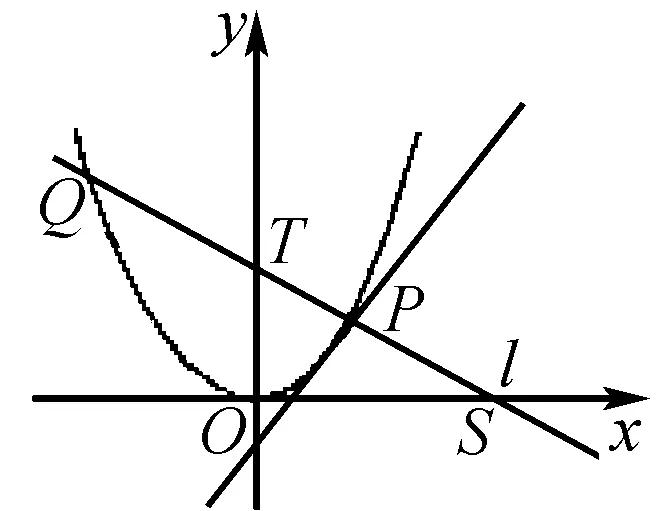
(1)若直线l与过点P的切线垂直，求线段PQ中点M的轨迹方程；

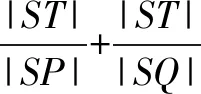
二、解析方法

本题是一道直线与抛物线的综合问题，将直线与直线的位置关系、直线与抛物线的位置关系结合起来，求解轨迹方程和范围问题.重点考查学生对数形结合、函数与方程、分类讨论和转化与化归思想的运用.笔者经过探究给出如下的证法：

(1)解析几何中求轨迹方程的常用方法有：①待定系数法；②直译法；③相关点法；④参数法；⑤交轨法.由于本题涉及中点，所以可考虑通过韦达定理或点差法建立中点的表达式，主要运用参数法求解轨迹方程.

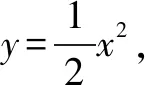
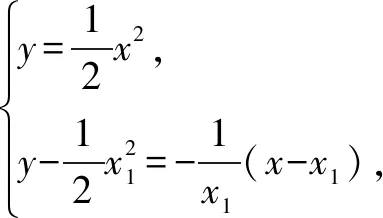
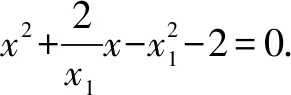
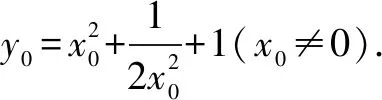
解法二点差法

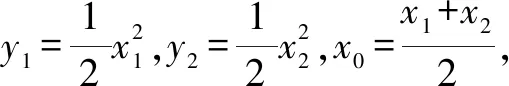
评注比较两种解法，解法一更常规，学生更容易运用，解法二容易被学生忽视.但解法二更简便，更巧妙，一旦掌握了点差法这种解题思路，强化中点弦意识，则解决这类问题会变得更简单.

(2)解析几何中的范围问题，涉及函数、导数、不等式等知识点，解题思路灵活，一直是高考重点考查的内容.常见的解决方法有：利用函数的思想，将所求问题转化为某个变量的函数，再用代数方法解决；利用基本不等式，通过等价转化问题为基本不等式型问题求解；利用方程的思想，注意二次方程判别式的运用.

解法一直接利用基本不等式放缩

解法二先代入再消元放缩

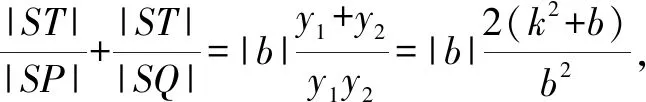
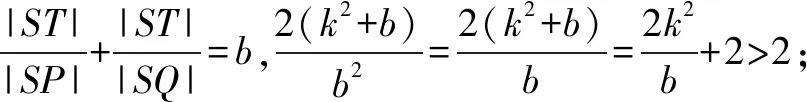
解法三先消元再用基本不等式放缩

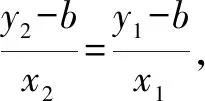
评注求解数学问题的策略很多，这就要求我们平时在解决数学问题时养成勤思考、勤总结的良好习惯.解决数学问题的策略很重要，有时一个问题，如果选择了恰当的方法和技巧，就会使问题解决变得十分容易，达到事半功倍的效果.反之，若选择的方法不恰当，则会使问题解决陷入十分繁杂的讨论或计算中.