浅谈函数思想在高中数学解题中的应用

崔 雷

(云南省昆明市第一中学西山学校 650100)

高中数学是高中教育的一门必修课程，其对于学生综合能力发展有极大影响.而由于高中数学知识抽象性比较强，很多学生在学习过程中会产生抵触心理，从而影响到高中数学教学效果，降低了学生解题效率.函数思想属于数学思想的一种，将其应用在高中数学解题中，可以极大地促进学生思维发展，便于学生高效率解题，有利于学生知识内化.

枸橼酸莫沙比利原料药（武汉顶辉医药科技有限公司，批号：20160526，纯度：＞99%）；十八醇（无锡海硕生物有限公司，批号：20150902）；丙烯酸树脂（德国Rohm公司，批号：20160318）；碳酸氢钠（批号：20151024）、滑石粉（批号：20160116）均购自重庆川江化学试剂厂；微晶纤维素（MCC，杭州高成生物营养技术有限公司，批号：20160318）；羟丙基甲基纤维素[HPMC，陶氏化学（中国）投资有限公司，批号：20160312]；柠檬酸三乙酯（潍坊迪蒙化工有限公司，批号：20160112）；其余试剂均为化学纯，水为去离子水。

我在回答有关教养问题的提问时，经常提到“让孩子有路可走”。许多妈妈向我表示：她们理解并接受这个亲子教育的“双赢策略”理念，但是在实行的时候，就发现问题不简单。妈妈们在摸不到门径时就问我：“究竟路在何方？”

一、函数思想

量量之间的关系为函数思想的体现，该种关系具有一定的变化性，并不是稳定不变的.函数的本质为对应，如函数y=f(x)，其构成的基本要素为对应法则f和自变量范围，其中占据主导地位的是自变量.就函数的值域来讲，决定的因素为定义域和对应法则.

采用函数思想解决高中数学问题时，一般是通过建立相应的辅助函数来解决，其主要是将数学问题转变为相应的函数问题，之后对函数进行相应的处理，最终获得正确结果.在解决数学问题中，函数思想的运用包含以下几个方面：(1)整体法，整体处理高中数学问题的整体形式和结构，这样使得整个题目变得较为简单明了；(2)递推思想法，其主要是构建、探究和应用高中数学问题中牵涉的递推关系，对有关的数学问题进行处理解决，主要应用在数列这一知识块中；(3)归纳假设法，在探索问题过程中，归纳假设法较为常见.首先通过归纳猜想的方法尝试和观察数学试验，之后通过不完全归纳方法归纳假设数学问题，最后通过数学归纳方法证明自己假设的数学问题.

1.不等式中函数思想的应用

二、函数思想在高中数学解题中的应用

在解决高中数学问题时函数思想被广泛的应用，其能很好地解决不等式、数列、方程等问题.

血清IL-2、IFN-γ、TNF-α与IGF-1水平：2组患者于治疗前和治疗4周期后空腹采静脉血5 mL，离心取血清于-80 ℃储存，采用酶联免疫吸附法(ELISA)测量患者血清IL-2、IFN-γ、TNF-α与IGF-1水平。

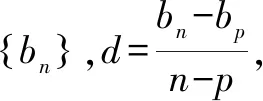
3.数列中函数思想的应用

函数方程思想为数学思想组成部分中的主要成员，在一些数学领域中，函数同方程之间具有较为紧密的联系，函数中包含方程，方程在函数中为不可缺少的一部分，针对该种现象的出现，在解决方程问题时采用函数思想为一种有效的、可行的方法.例如：解方程(x2-x+1)5-x5+4x2-8x+4=0.分析：题目中的方程为一元五次方程，一般在高中数学中，很少出现这种题目，通过函数思想对其进行变形，能有效降低该题目的难度.解：将原方程进行变形，设x2-x+1=t，因函数f(t)=t5+4t在R上单调递增，又因为f(x2-x+1)=f(x)，所以x2-x+1=x，得到x=1.因此，方程(x2-x+1)5-x5+4x2-8x+4=0有唯一实数解x=1.该题在高中数学中属于较难处理的高次方程，通过构建单调函数，并通过单调函数的函数值同自变量之间的一一对应关系进行处理，这样便能将较为复杂的问题简单化，最终简单地解决该问题.

2.方程中函数思想的应用

在高中数学科目中，不等式证明占据重要地位.在解决不等式问题中，函数思想的运用就是研究函数正负区间、单调性和零点等问题.因此，教师在课堂上指引学生通过函数思想处理不等式问题，能很好地、便捷地正确处理问题.例如：假设a,b,c∈R，且它们的绝对值均不大于1，求证：ab+bc+ca+1≥0.分析：一般学生在看到该题目时，仅通过题目给出的已知条件很难着手.但如果从其他角度出发，通过构造函数，就能将题目中的不等式转变为函数问题，进而使得题目变得较为简单.构造函数f(a)=ab+bc+ca+1，该函数为关于a的一次函数，因为a∈[-1,1]，所以只要证明f(-1)≥0，并且f(1)≥0，那么就能证明f(a)≥0.证明：假设f(a)=ab+bc+ca+1，则该函数为关于a的一次函数.因为a,b,c∈[-1,1]，所以f(1)=b+bc+c+1=b(1+c)+(c+1)=(b+1)(c+1)≥0，f(-1)=-b+bc-c+1=-b(1-c)+(1-c)=(1-b)(1-c)≥0，所以，f(a)在区间[-1,1]上恒为非负数，所以，ab+bc+ca+1≥0.学生在解决该题时应具备一定的函数思想，通过构造一次函数，利用其单调性，证明在区间[-1,1]上恒为非负数，就能证明ab+bc+ca+1≥0.

4.实际优化问题中函数思想的应用

在高中数学课堂教学中，利用函数思想还可以更好地引导学生对实际问题进行解决，因此，在进行高中数学实际问题解决中，教师还应该引导学生合理地应用函数思想，将复杂、综合、系统的数学问题转变成简单的数学问题，便于学生解答.如在我们现实生活中，有很多关于量与量的关系，如路程问题，其需要考虑到速度、时间、路程等的相互关系；如生产问题，需要考虑到单价、总数、时间的相互关联；即便是价格问题、采购问题也涉及到函数 变量.同时在当前的高考中，实际问题的所占比具有很高的比重，教师必须引导学生学会利用函数思想来解决实际问题，以此提高学生的解题效率.另外，很多高中数学实际问题都需要利用函数图象辅助解答，因此教师还需要引导学生学会利用函数图象形式将变量关系展现出来，引导学生可以对问题进行深入研究.

农村留守儿童教育问题已经成为社会重要问题，对于政府来说，首先要扩大宣传力度，贯彻落实义务教育，强化政府相关部门的协调作用，及时掌握农村留守儿童的分层信息，因地制宜地开展工作，并鼓励有爱心的个人和社会团体参与到关爱留守儿童的行列中。

综上所述，在高中数学解题中，利用函数思想可以极大地促进学生逻辑能力发展，提高了学生的数学学习积极性，同时也提升了学生解决实际数学问题的准确性，促进了学生数学学习能力提升.因此，在实践中，高中数学教师要特别注重引导学生将函数思想应用到解题活动中，不断提高学生数学学习成绩.