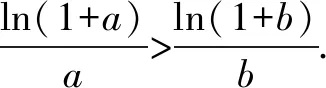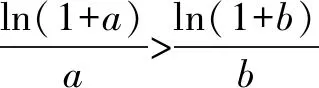例析二元不等式的求解策略

张云燕 指导老师:许万成

(江苏省建湖县第二中学高三10班 224700)

近年来在高考试题以及各地高三的模拟测试中，经常出现涉及两个变量的不等式问题，同学们面对这类问题时常常感觉无从下手，找不到解题的突破口.针对上述情况，笔者根据自己平时的做题实践，结合有关例题向同学们介绍几种常见的求解策略，希望能够给同学们的学习提供帮助.

一、利用基本不等式处理

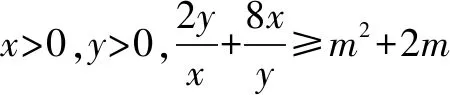
答案：-4≤m≤2

二、利用待定系数处理

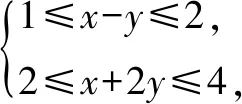
解设4x-2y=λ(x-y)+μ(x+2y)=(λ+μ)x+(2μ-λ)y，

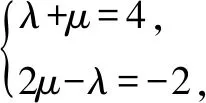
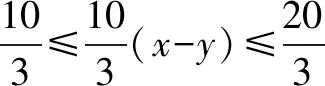
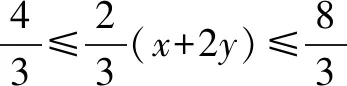
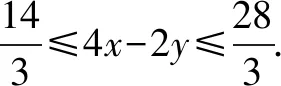
三、利用线性规划处理

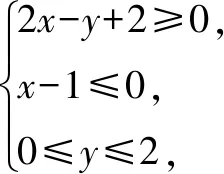
值范围是____.

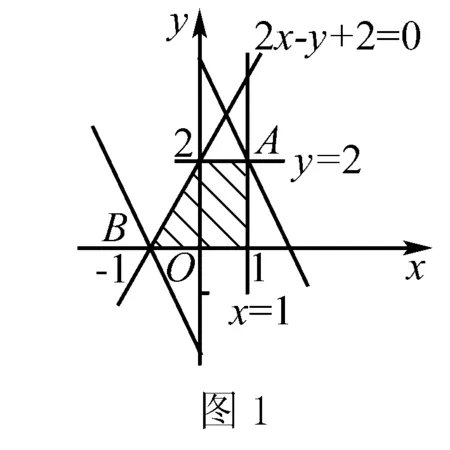
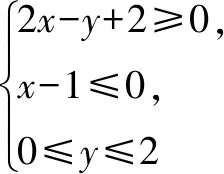
向量a=(2,1)，向量b=(x,y)，a·b=2x+y，设z=2x+y即y=-2x+z.

由图可以y=-2x+z是平行直线系，z为该平行线系的纵截距，当直线过点A(1,2)时z取最大为4，当直线过点B(-1,0)时z取最小-2.故a·b的取值范围是[-2,4].

答案：[-2,4].

四、利用消元法处理

在两个变量的条件不等式问题中，可以利用题中条件将一个变量用另一个变量表示出来，这样一来可以将二元不等式转化为一元不等式来处理.

例4已知正实数x,y满足xy+2x+y=4，则x+y的最小值为____.

分析所给条件xy+2x+y=4，可以用x来表示y，然后代入x+y，将x+y转换成只含有x的代数式，以达到求解的目的.

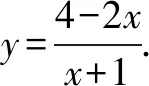
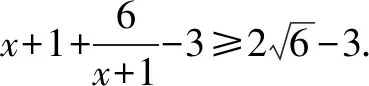
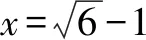
五、分离参数法处理

有些含有参数C的不等式问题，经过等价变形，能够分离出参数C，那么可化成C≥(≤)f(x,y)的形式，从而转化成求f(x,y)的最大(小)值的问题.

例5若不等式x2-2y2≤cx(y-x)，对任意满足x>y>0的实数x,y恒成立，则c的最大值为____.

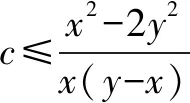
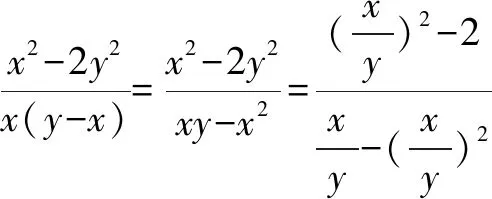
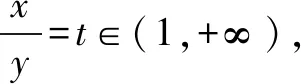
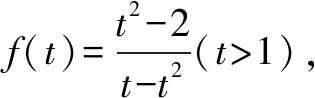
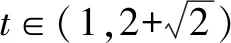
六、主元法处理

在多个变量问题中，可以将问题中的一个变量看成未知数，另一个变量当成常数，这样就将多元问题转化成一元问题来处理.

例6证明伯努利不等式：n∈N*，当x>-1时，有(1+x)n≥1+nx.

分析伯努利不等式(1+x)n≥1+nx中有两个变量x,n,从变量x的角度可以构造函数，利用函数的性质来证明.

证明当n=1时，不等式显然成立

当n≥2时，令g(x)=(1+x)n-nx-1,则g′(x)=n(1+x)n-1-n=n[(1+x)n-1-1].

令g′(x)=0,得x=0.

当-1

当x>0时，g′(x)>0,g(x)是增函数.

所以g(x)≥g(0)=0,故当x>-1时，有(1+x)n≥1+nx.

七、构造形似函数法处理

当两个变量可以分离时，可以根据不等式两边结构构造函数，利用函数的单调性来解决问题.

例7若0(1+b)a.

分析所证(1+a)b>(1+b)a为变量a,b的指数式，可以通过取对数，然后分离两个变量来构造函数证明.

综上原命题成立.