关于转化思想方法在高中数学解题中的应用探讨

蔡永刚

(云南省昆明市第一中学西山学校 650100)

转化思想是众多数学思想中常用的一种方式，其可以引导学生把未知的知识、问题，转变成已知的知识、内容，从而更加顺利地解决问题.因此，在实际教学中，高中数学教师要特别注重培养学生的转化思想，使得学生可以更加快速、准确地完成解题.

一、三角函数中解题的应用

在解三角函数题中，转化思想主要是将复杂的三角函数问题转变为简单的问题，这样便于学生更快更简单地解决问题.如下例子：如果直线3x+4y+m=0同圆(x=1+cosθ,y=-2+sinθ)之间无公共点，求实数m取值范围.解：根据题目给出的条件，通过转化思想对本题进行复杂简单化，可转变为3cosθ+4sinθ=5-m，已知直线同圆无公共点，且-5≤3cosθ+4sinθ≤5，所以，5-m>5或5-m<-5.得到m<0或m>10.

二、圆锥曲线中解题的应用

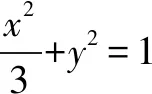
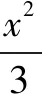
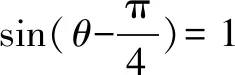
圆锥曲线中填空题和选择题等多是采用定义转化的方法进行解题.在抛物线中，若给出的条件为点到焦点距离，就应该转变为点到准线的距离；若给出的条件为点到准线的距离，就应该转变为点到焦点距离.在双曲线或是椭圆中，点到左右焦点的距离之间是可以相互转化的.在解决椭圆求最值问题时，通过椭圆参数方程转变成三角函数最值问题.

三、概率中解题的应用

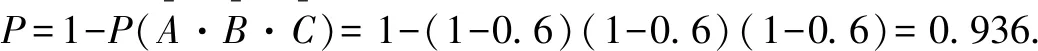
四、导数中解题的应用

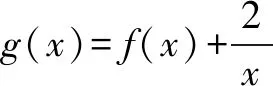
在高中导数这一部分中，存在问题和恒成立问题为常见的类型，a≤f(x)在定义域中恒成立，也就是a≤f(x)的最小值；a≥f(x)在定义域中恒成立，也就是a≥f(x)的最大值.如果存在x0属于定义域，a≥f(x0)成立，也就是a≥f(x)的最小值；如果存在x0属于定义域，a≤f(x0)成立，也就是a≤f(x)的最大值.导数中涉及的存在问题和恒成立问题转化为最值问题，就能很好地避免讨论含参不等式的讨论，使得复杂的运算变得简单化.

综上所述，在高中数学解题中，利用转化思想可以把复杂、困难的数学问题转变得更加简单、易懂，便于学生理解，同时也有助于学生数学学习积极性的提高.因此，在高中数学解题教学中，教师要结合学生的实际情况，培养学生转化思想，从而促进学生数学思维能力、解题能力的提升，满足学生的综合发展需求.