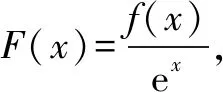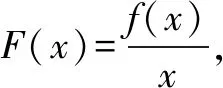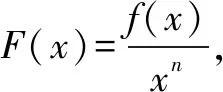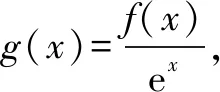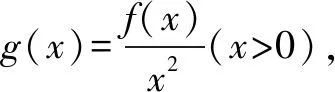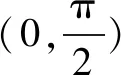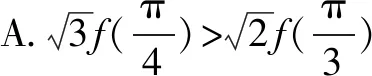构造辅助函数 破解导数中的抽象函数问题
罗文军 刘娟娟
(1.甘肃省秦安县第二中学 741600;2.甘肃省秦安县郭嘉镇槐川初级中学 741600)
破解导数中的抽象函数这类试题,准确构造出符合题意的辅助函数是解题的关键.构造函数时往往从两方面着手:①根据导函数的“形状”变换不等式“形状”;②若是选择题,可根据选项的共性归纳构造恰当的函数.本文对这类试题进行总结.
一、构造差函数
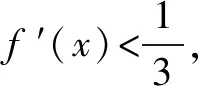
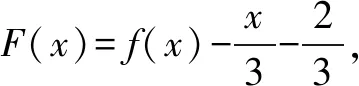
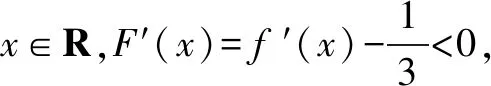
例2函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为____.
解析构造函数g(x)=ex·f(x)-ex,因为g′(x)=ex·f(x)+ex·f′(x)-ex=ex[f(x)+f′(x)]-ex>ex-ex=0,所以g(x)=ex·f(x)-ex为R上的增函数.又因为g(0)=e0·f(0)-e0=1,所以原不等式转化为g(x)>g(0),解得x>0.
二、构造可导的乘积函数
根据导数的运算法则,当F(x)=f(x)·g(x)时,则F′(x)=f′(x)g(x)+f(x)g′(x),不难得出以下结论:
1.若f′(x)+f(x)≥0(或≤0),构造F(x)=exf(x),则F′(x)=ex[f′(x)+f(x)]≥0(或≤0);
2.若xf′(x)+f(x)≥0(或≤0),构造F(x)=xf(x),则F′(x)=xf′(x)+f(x)≥0(或≤0);
3.若xf′(x)+nf(x)≥0(或≤0),构造F(x)=xnf(x),则F′(x)=xn-1[xf′(x)+nf(x)]≥0(或≤0)(注意对xn-1的符号进行讨论).
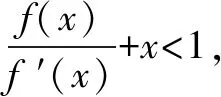
A.对于任意x∈R,f(x)<0
B.对于任意x∈R,f(x)>0
C.当且仅当x∈(-∞,1)时,f(x)<0
D.当且仅当x∈(1,+∞)时,f(x)>0
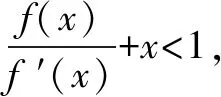
又因为f(x)是定义在R上的减函数,所以f(1)>0.
综上所述,对于任意x∈R,f(x)>0,故选答案B.
例4函数f′(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x<0时,xf′(x)+f(x)>0,则使得f(x)<0成立的x的取值范围是( ).
A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)
C.(-∞,-1)∪(1,+∞) D.(-1,0)∪(0,1)
解析设g(x)=xf(x),则g′(x)=xf′(x)+f(x).因为,当x<0时,xf′(x)+f(x)>0,所以当x<0时,g′(x)>0,所以函数g(x)=xf(x)在(-∞,0)上为增函数.因为函数f(x)是奇函数,所以g(-x)=(-x)f(-x)=(-x)[-f(x)]=xf(x)=g(x),所以g(x)为定义域上的偶函数,所以g(x)在(0,+∞)为减函数.由f(1)=0,得g(1)=0,g(-1)=0.
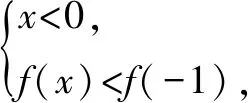
例5已知定义域为{x|x≠0}的偶函数f(x),其导函数为f′(x),对任意正实数x满足xf′(x)>-2f(x),则不等式x2f(x) 例7已知f(x)是定义在区间(0,+∞)内的函数,其导函数为f′(x),且不等式xf′(x)<2f(x)恒成立,则( ). A.4f(1) C.f(1)<4f(2) D.f(1)<4f′(2) 例9若对定义在R上的可导函数f(x),恒有(4-x)f(2x)+2xf′(2x)>0,(其中f′(2x)表示函数f(x)的导函数f′(x)在2x的值),则f(x)( ). A.恒大于等于0 B.恒小于0 C.恒大于0 D.f(x)与0 的大小关系不确定 由题设(4-x)f(2x)+2xf′(2x)>0可知,当x>0时,g′(x)>0,g(x)在(0,+∞)上单调递增,当x<0时,g′(x)<0,g(x)在(0,+∞)上单调递减,所以当x≠0时,g(x)>g(0)=0,所以x≠0时,f(2x)>0.在(4-x)f(2x)+2xf′(2x)>0中令x=0时,知f(0)>0. 综上所述,f(x)>0对任意的x∈R恒成立,故选答案C. 例10已知定义在R上的奇函数f(x)的导函数为f′(x),当x<0时,f(x)满足2f(x)+xf′(x) A.5 B.3 C.1或3 D.1 由题设,当x<0时,2f(x)+xf′(x)-xf(x)<0,所以F′(x)>0,F(x)在(-∞,0)上为增函数,F(x)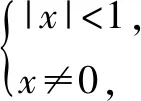
三、构造商函数