基于广义波阻抗梯度飞片的准等熵压缩技术*
陈子博,谢普初,刘东升,陈 伟,王永刚
(宁波大学冲击与安全工程教育部重点实验室,浙江 宁波 315211)
梯度功能材料是两种或多种材料复合且成分和结构呈连续梯度变化的一种新型复合材料。波阻抗梯度功能材料(wave impedance functionally graded material,WIFGM)是一类较特殊的梯度功能材料,该材料引起人们的关注始于材料高压本构和状态方程研究[1-2]。在轻气炮实验中,波阻抗梯度功能材料制作的飞片在高速碰撞靶材后,可以在靶材中产生具有缓慢上升前沿的压缩加载波,实现对靶材的准等熵压缩加载,熵增和温升远小于冲击绝热压缩情况。准等熵压缩加载填补了准静态等熵加载和冲击绝热加载之间空白,提供了一种考察物质压缩形态(尤其是偏离Hugoniot状态)的新实验途径,可以得到范围更广、压缩度更高、精度更高的材料物态方程参数。另外,把波阻抗梯度飞片的准等熵压缩性和二级轻气炮相结合可以发展三级炮超高速发射技术,弹丸速度可以达到10 km/s以上[3],这在航天器空间碎片防护领域具有重要的应用背景。
20世纪80年代,美国圣地亚核武器国家实验室首先开展了波阻抗梯度材料的制备技术研究。Barker等[1]采用颗粒共沉降成型结合高压粘接方法制备了Ta/Cu/Al/TPX金属-聚合物体系的波阻抗梯度飞片,可以在靶材中产生准等熵压缩波,但该波阻抗梯度飞片的力学强度较差,在发射过程中飞片易发生破坏。Chhabildas等[2]采用焊接方法制备了Ta/Cu/Ti/Al/Mg/TPX体系叠层飞片,但该飞片的波阻抗沿厚度方向是以阶跃方式变化的,导致其产生的压力剖面平顺性较差。后来,美国劳伦斯利弗莫尔国家实验室Martin等[4]采用流延成型法制备了7种组分和19种组分的Mg/Cu体系波阻抗梯度材料,获得了平滑的压力剖面。近来,Yep等[5]进一步发展了流延成型技术,制备了近100种组分的Mg/Cu/W体系梯度飞片,其具有更宽广波阻抗变化范围,可以实现500 GPa压力值的准等熵压缩。从20世纪90年代开始,武汉理工大学和中国工程物理研究院流体物理研究所合作开展波阻抗梯度材料制备技术研究[6-8],发展了放电等离子快速粉末烧结法,研制出的梯度飞片已成功应用于准等熵压缩加载、超高速驱动、太帕量级压力的高精度平面加载以及复杂加、卸载等动高压实验技术领域。传统的波阻抗梯度功能材料制备多是选择多种不同密度不同波速的金属材料进行复合。为了得到材料波阻抗准连续变化,需要进行非常多组分配比,铺层和烧结制作工序异常繁杂,质量也难以精确控制,成品率低,价格昂贵,这大大制约了波阻抗梯度功能材料实际应用,迫切需要发展新的制备工艺。最近,Taylar等[9]采用激光立体光刻技术制备了波阻抗梯度陶瓷飞片,实现对平板撞击实验中冲击加载波形的有效调控。
增材制造(additive manufacturing, AM)技术是基于计算机辅助设计数据,采用材料逐层累积的方法来制造零件[10-11]。材料结构的计算机三维自由设计和增材制造技术的完美结合为新型功能材料或结构材料的研发与制备提供新的途径。本文中拟采用激光选区熔化(selective laser melting,SLM)金属增材制造技术,通过几何结构设计来研发新型的广义波阻抗梯度飞片材料。首先,基于应力波传播理论来探讨波阻抗梯度飞片的几何构型设计;随后对“结构设计型”波阻抗梯度飞片的准等熵压缩加载特性进行数值模拟,重点讨论结构设计的关键参数和碰撞速度对加载波形的影响规律;最后,采用增材制造技术制备波阻抗梯度飞片,开展气炮实验,对比分析了实验与数值计算结果,验证新型波阻抗梯度飞片的设计可行性和适用性。
1 波阻抗梯度飞片的结构设计
材料密度ρ0与波速c的乘积定义为材料波阻抗。在研究变截面杆中波传播问题时人们引入广义波阻抗的概念,定义为材料密度ρ0、波速c以及截面面积A的乘积。由此来看,除了改变材料密度和波速之外,还可以通过改变截面面积来实现广义波阻抗的梯度变化。王礼立等[12]通过引入广义波阻抗把锥形杆中的纵波传播问题近似化为一维应力平面纵波问题来处理,通过特征线方法探讨了应力波在锥形杆中的传播规律,结果表明,锥形杆具有调节应力波波形和强弱的特性。罗鑫等[13]对锥形杆共轴撞击进行数值分析,结果表明,撞击所产生的加载波阵面具有较长的前沿升时,同时还消除了波形振荡。陶俊林等[14]在SHPB实验中将圆柱形子弹改变为锥形子弹,实现对一维应力条件下加载波形的调整,上升沿时间显著增大。受此启发,在轻气炮实验中也采用类似的设计思想。轻气炮实验系统中采用薄板飞片作为加载手段,以便在样品中产生一维冲击波,因此不可以直接把薄板飞片改变为锥形飞片。这里,我们把飞片分为两部分,一部分作为飞片基座,然后在基座上密排叠加许多小正四棱锥台,犹如基座上长出一根根变截面针刺,简称为“针床型”波阻抗梯度飞片,其几何结构示意图如图1所示,图中e为基座高,h为四棱锥台高,m为正四棱锥台下底边宽,n为正四棱锥台上顶边宽。当“针床型”波阻抗梯度飞片高速撞击样品时,每一个小正四棱锥台都可以看作“点”加载脉冲源,会产生一系列具有缓慢上升前沿的类球面波,随着传播距离增大球面波将相互叠加,最终可以得到近似平面的加载波形,从而满足一维应变加载条件。
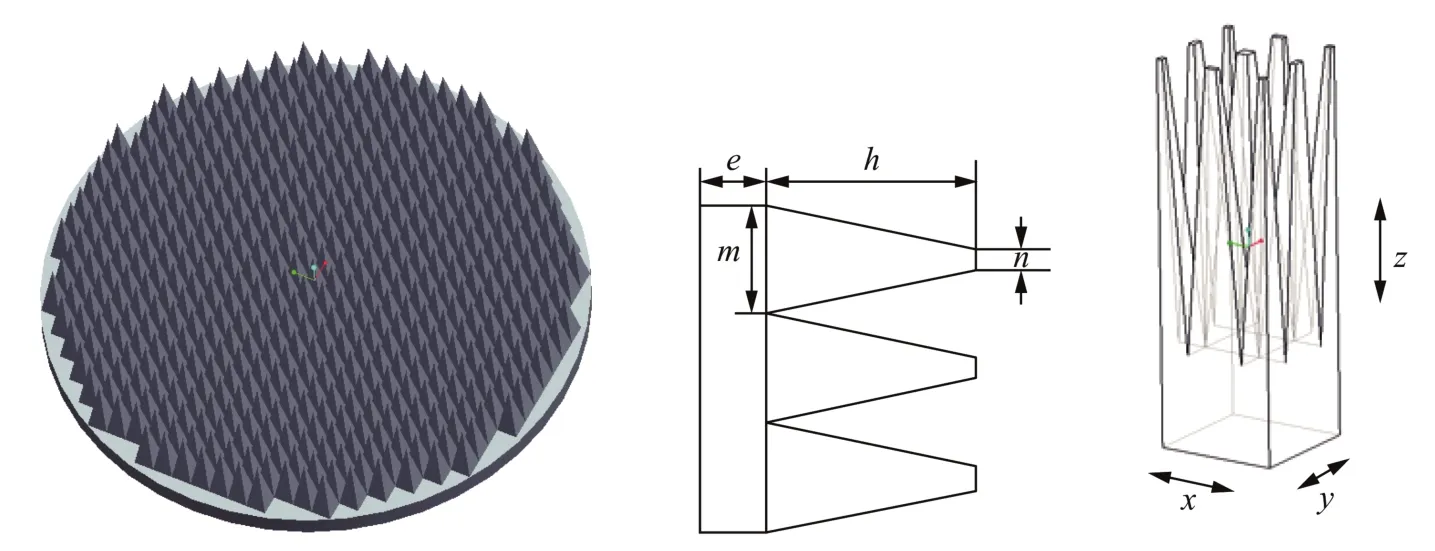
图1 “针床形”广义波阻抗梯度飞片几何结构示意图Fig.1 Schematic diagram of the “needle-bed” generalized wave impedance gradient flyer
2 计算模型
为了验证上述设计思想的可行性,首先开展“针床型”波阻抗梯度飞片高速撞击靶板的数值模拟。在数值计算之前,还需要选择合适的算法。如果采用拉格朗日算法,在“针床型”波阻抗梯度飞片高速碰撞靶板时,飞片和靶板都会产生由于局部接触引起局部大变形,从而导致局部网格单元发生畸变问题,使得计算提前中止。通常的解决方案是采用侵蚀算法,把严重畸变的网格单元从模型中删除,但网格单元删除降低了计算精度。为了解决大变形网格畸变问题,人们常采用欧拉算法或者光滑粒子流体动力学(SPH)算法。相比拉格朗日算法,虽然欧拉算法解决了网格畸变问题,但更加耗费机时。本文中拟采用SPH算法来计算“针床型”波阻抗梯度飞片高速碰撞靶板问题。SPH算法是将连续的固体离散为一系列具有质量、速度和能量的粒子,通过求解质点组的动力学方程和跟踪每个质点的运动轨道求得整个系统的力学行为。该方法是一种无网格拉格朗日数值计算方法,广泛应用于处理大变形问题。
“针床型”波阻抗梯度飞片上有非常多的小正四棱锥台,周期性排列。小正四棱锥台顶面尺寸非常小,为了保证足够的计算精度,建模时需要划分许多尺寸非常小粒子,整个模型的粒子数庞大,计算耗费时间非常长。为此,这里采用了简化模型,即选择一个典型单胞来计算,单胞SPH计算模型如图2所示,通过在x轴和y轴方向设置固定边界条件来保证仅仅z轴方向发生应变,以满足一维应变加载条件。典型计算单胞的边长为2 mm,基座高2 mm,正四棱锥台的底边宽1 mm、顶边宽0.2 mm、高6 mm,靶板边长2 mm、高7 mm。模型中SPH粒子的直径为100 μm。由于高速碰撞的物理过程,目前计算中常采用Johnson-Cook本构模型,具体包含线性热弹性、Mises屈服准则、各向同性应变硬化、应变率硬化、各向同性损伤引起的软化,其等效Mises屈服应力表示如下:

式中:A、B、n、C和m是模型常数; εeq是等效塑性应变是无量纲化等效塑性应变率,为参考应变率;T∗=(T-T0)/(Tm-T0)为无量纲温度,其中T0是室温,Tm是材料的熔点。计算时波阻抗梯度飞片和靶板材料均为钢,表1给出了数值模拟中采用的材料本构模型参数。

图2 波阻抗梯度飞片气炮实验的SPH单胞计算模型Fig.2 SPH cell simulation model of impedance gradient flyer in gas gun experiments

表1 飞片和靶板材料本构和状态方程参数Table 1 Flyer and target material parameters
3 计算结果讨论与分析
3.1 平面波产生和传播特性分析
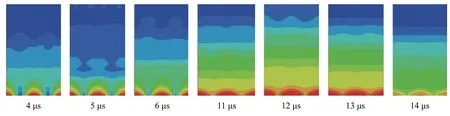
图3 靶板内不同时刻的应力波传播云图Fig.3 Stress wave propagation contours in the specimen at different times
首先通过一个算例来讨论一下“针床型”梯度飞片高速撞击靶板后靶板中应力波传播特性。图3给出了撞击速度350 m/s下靶板中沿z轴方向传播的不同时刻的压力云图。初始阶段可以清楚地看到每一个小四棱锥台接触处产生了球面加载波,彼此独立往前传播;随着传播距离增大,球面加载波开始相互作用;随着传播距离进一步增大,最后可以看到开始的球面波逐渐转变为平面波,从而实现对靶板平面加载。在实际应用中,为了保证靶板承受的是平面加载,需要在靶板前增加背板。
3.2 撞击速度和几何结构参数的影响
3.2.1 撞击速度
首先讨论飞片撞击速度对准等熵压缩加载特性的影响。计算中,保持典型单胞几何结构参数不变,仅仅改变飞片撞击速度。图4给出了350 m/s速度下不同时刻飞片和靶板的变形过程和塑性应变云图,从图中可以看到:(1) 飞片上的小四棱锥台与靶板的接触处首先出现了比较严重的塑性变形,塑性变形区随着时间逐渐增大;(2) 小四棱锥台之间间隙不断被由于严重塑性变形而破损的物质填充,小四棱锥台的高度不断减小,其整体压缩量超过50%。图5给出了200、350、500、800 m/s撞击条件下靶板自由面速度时程曲线,从图中看到:(1) 靶板中产生了缓慢上升的加载波形,在初始阶段自由面速度波形出现了一些振荡,但随着速度增大,振荡现象逐渐转弱,速度时程曲线趋于光滑,同时还观察到初始的振荡现象还依赖于飞片撞击速度,高速碰撞时振荡现象比较微弱,且持续时间比较短;(2) 加载波形的上升沿时间随着飞片撞击速度的增大而不断减小。自由面速度初始振荡现象和上升沿时间对撞击速度的依赖性主要归因于飞片的塑性变形过程及塑性波传播。图6给出了不同撞击速度下飞片最终变形图,随着撞击速度增大,小四棱锥台压缩量不断增加。
图7给出了自由面速度波形的上升沿时间随着撞击速度的变化曲线,结果显示两者之间呈指数衰减关系,拟合方程为:

图4 不同时刻飞片和靶板的塑性应变云图Fig.4 Plastic strain contours in the flyer and specimen at different times

式中:t为自由面速度波形的上升沿时间,v0为飞片的撞击速度。另外,靶板自由面速度峰值也依赖于飞片撞击速度。图8给出了自由面速度的峰值与撞击速度的比值随撞击速度的变化曲线,随着撞击速度增大,自由面速度的峰值更接近于撞击速度,比值趋近于1,两者之间呈指数增长关系,拟合方程为:

式中:vmax/v0为靶板自由面速度峰值与飞片撞击速度比,v0为飞片的撞击速度。

图5 不同撞击速度下靶板自由面速度时程曲线Fig.5 Free surface velocity profiles of specimen at different impact velocities

图6 不同撞击速度下飞片变形的最终形态Fig.6 Final deformation of the flyer at different impact velocities
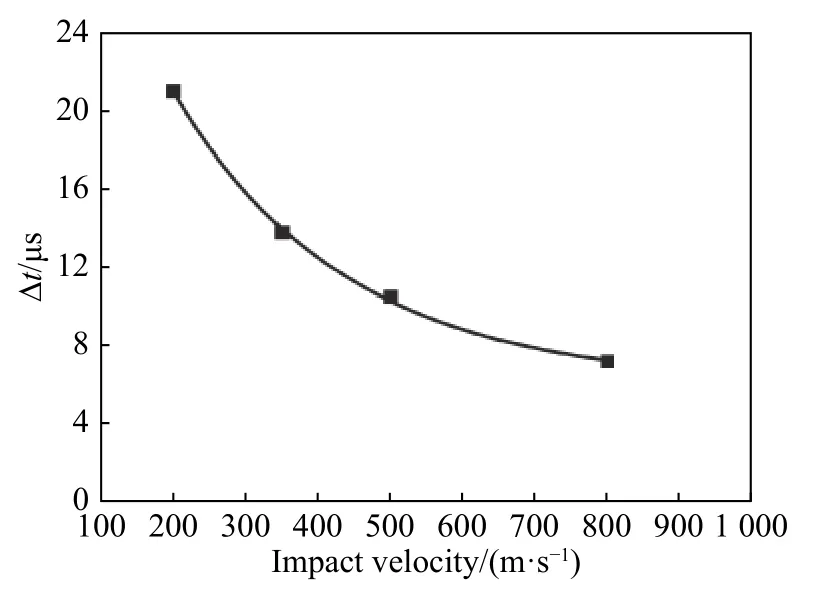
图7 压缩波上升沿时间随着撞击速度的变化曲线Fig.7 Compression wave front time vs.impact velocities
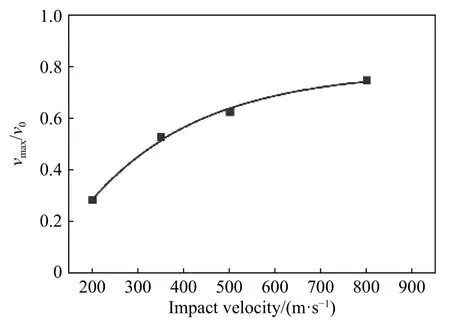
图8 自由面速度峰值与撞击速度比值随着撞击速度的变化曲线Fig.8 Ratios between peak velocity and impact velocity vs.impact velocity
3.2.2 几何结构参数
除了上述的飞片撞击速度,“针床型”飞片的几何结构参数也对准等熵压缩加载特性有显著的影响。首先讨论小四棱锥台高度的影响。其他几何参数不变条件下,四棱锥台高(h)分别选择6、8、10 mm,以相同撞击速度(350 m/s)撞击靶板。图9给出了靶板自由表面速度时程曲线,从中看到加载波形的上升沿时间随着锥台高度增加而增大,但速度峰值随着锥台高度增加而减小。接着,讨论小四棱锥台锥角的影响,这里定义正四棱锥倾斜面与底面夹角称为锥角,如图10所示,保持小四棱锥台上底边宽度不变,通过改变下底边边长来实现。下底边边长分别取 1、1.5、2和 3 mm,对应锥角分别为 86.2°、83.8°、81.4°、76.9°。图11给出了相同撞击速度(350 m/s)不同锥角条件下靶板自由面速度时程曲线的对比,图中显示:上升沿时间随着锥角增大而减小,但峰值速度随着锥角增大而增大。
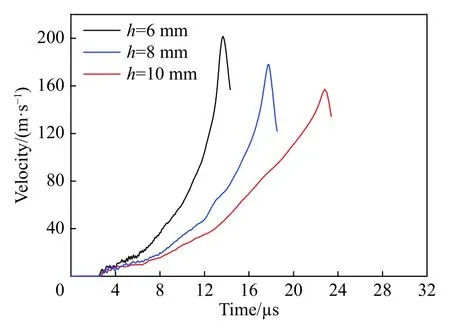
图9 不同四棱锥台高条件下靶板自由面速度时程曲线对比Fig.9 Comparison of the free surface velocity profiles for the specimen with different heights of the pyramid
图12(a)~(b)分别给出了上升沿时间和峰值速度随锥角的变化关系曲线,上升沿时间随锥角增大呈线性减小关系,拟合关系式为:
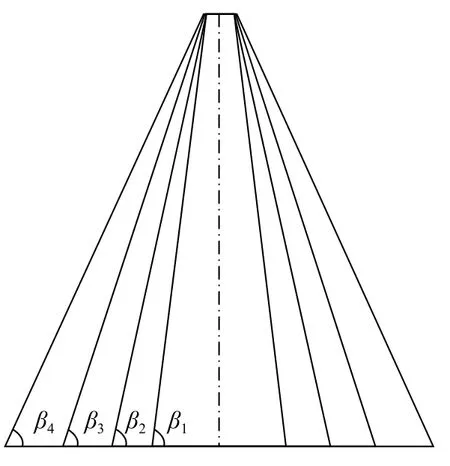
图10 四棱锥台的锥角定义示意图Fig.10 Schematic diagram of the cone angle of the pyramid
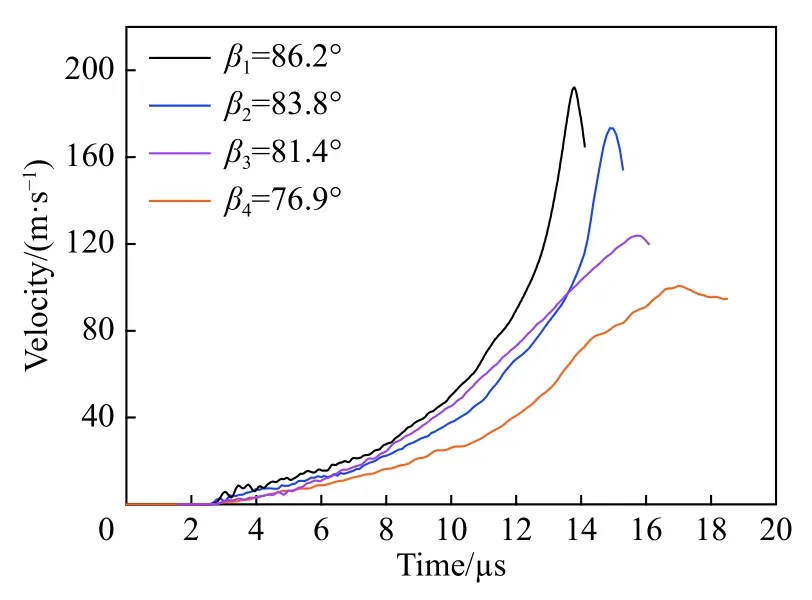
图11 不同锥角条件下靶板自由面速度时程曲线对比Fig.11 Comparison of free surface velocity profiles for the pyramid specimen with different cone angles
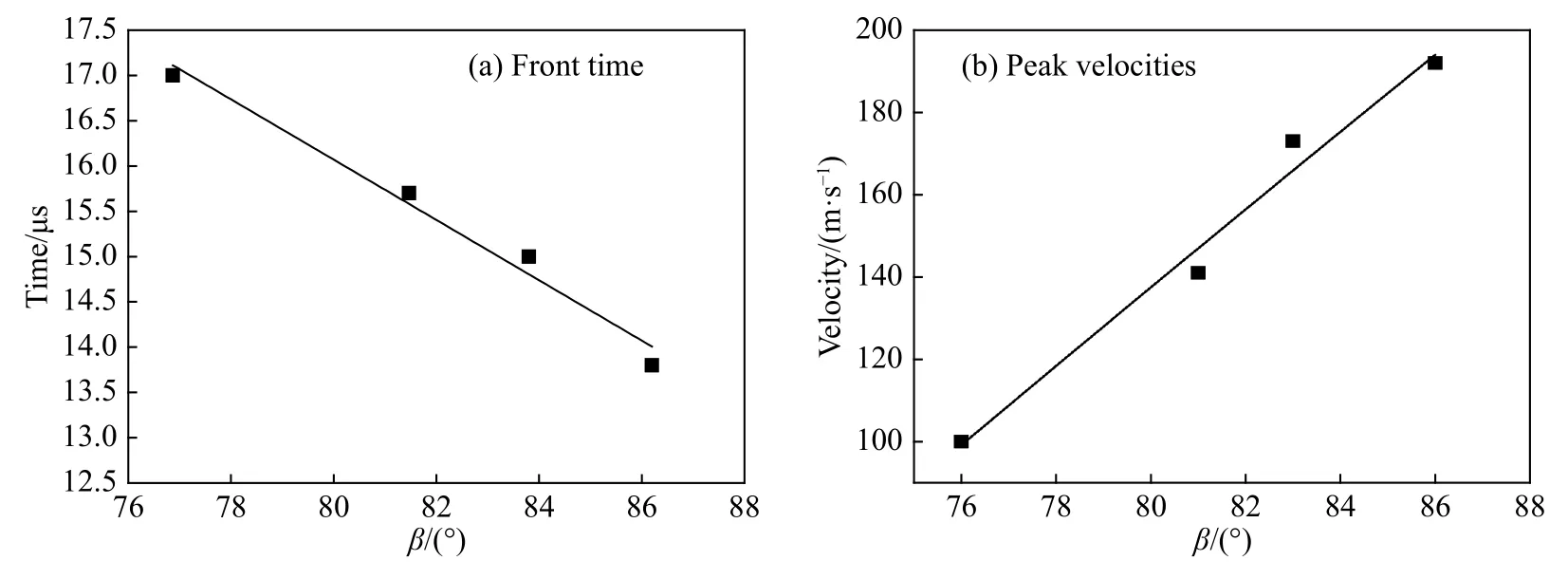
图12 压缩波上升沿时间和峰值速度随着正四棱锥台锥角的变化曲线Fig.12 Compression wave front time and peak velocity vs.the cone angle of the pyramid

而峰值速度与锥角之间呈线性增长关系,拟合关系式为:

式中:t表示波阵面前沿上升沿时间,μs;β表示梯度飞片正四棱锥倾斜面与底面夹角形成锥角;vmax为靶板自由面速度峰值,m/s。
最后讨论正四棱锥台的上底边宽的影响。保持下底边和锥台高度不变,上底边宽分别为0.2、0.4和0.6 mm,以相同初始速度(350 m/s)冲击靶板。图13给出了不同上底边宽带条件下的靶板自由面速度的时程曲线,从图中可知:自由面速度曲线初始阶段出现了明显的台阶,随着上底边宽度增大,台阶高度也增大,为了获得比较平顺的准等熵压缩加载条件,四棱锥台上底边宽度不易过大;同时上底边宽度也影响着上升沿时间,宽度增大,上升沿时间变小。
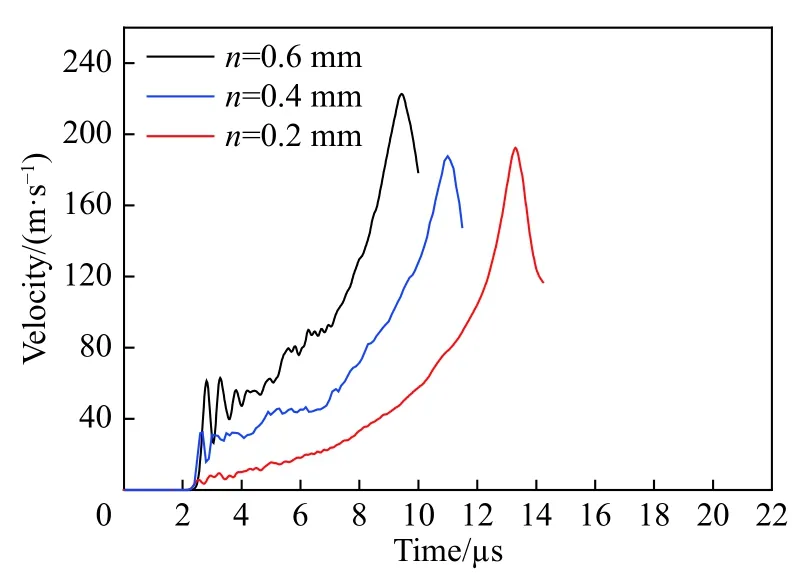
图13 不同上底边宽度条件下靶板自由面速度时程曲线对比Fig.13 Comparison of free surface velocity profiles for the specimen with different widths of the upper edge
4 实 验
4.1 广义波阻抗梯度飞片制备
利用Pro-E软件建立了广义波阻抗梯度飞片三维模型,如图14(a)所示,飞片直径53 mm,厚8 mm,基座高2 mm,四棱锥台高6 mm,正四棱锥台下底边宽2 mm。采用德国EOS—M280激光选区熔化金属3D打印机进行制备,粉末材料采用GP1不锈钢粉末,制备完成的飞片如图14(b)所示。

图14 广义波阻抗梯度飞片的3D几何模型和样品Fig.14 3D model and product of generalized wave impedance gradient flyer
4.2 气炮实验
实验在一级轻气炮上进行,实验装置示意图如图15所示,为了保证击靶平面性,飞片安装于铝合金弹托上,通过高压气体驱动弹托和飞片高速撞击靶板,飞片击靶速度由测速探针来测量,采用全光纤激光位移干涉系统(DISAR)来监测靶板自由面速度时程曲线。实验中测得飞片撞击速度为348 m/s。图16给出了实测的靶板自由面速度时程曲线。按照实验条件开展了相关的数值模拟工作,计算结果与实验结果的对比也如图16所示,两者基本一致,从而验证了设计思想和数值计算的有效性。
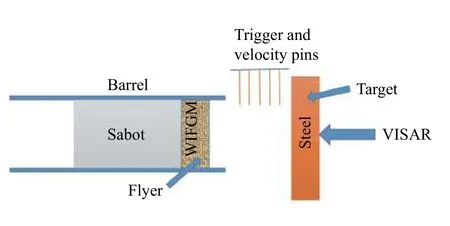
图15 轻气炮实验装置示意图Fig.15 Schematic of the gas gun device
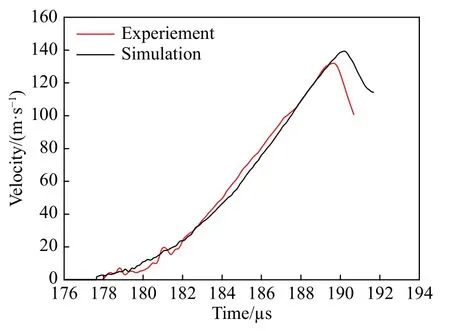
图16 实验与数值计算得到靶板自由面速度时程曲线对比Fig.16 Experimental and numerical free surface velocities of the target
5 结 论
(1) “针床型”小四棱锥台高速碰撞靶板后,在靶板中产生密集分布的球面加载波,随着传播距离的增大,球面加载波相互叠加形成缓慢上升前沿的平面加载波,从而实现对靶板的准等熵压缩加载;
(2) 准等熵压缩加载的特性强烈依赖于飞片击靶的速度,随着速度的增加,加载波上升沿时间减小,而峰值速度增大;
(3) 广义波阻抗飞片的关键几何参数也对准等熵压缩加载特性影响显著,随着四棱锥台高增大,加载波上升沿时间增长,而峰值速度减小;相反,保持四棱锥台高不变,只改变锥角的大小,随着锥角的增大加载波上升沿时间缩短,而峰值速度增大;小四棱锥台变钝(即上底边宽度增大)会导致加载波初始阶段出现明显的台阶,为了获得比较平顺的准等熵压缩加载条件,四棱锥台需要保持尖锐度。

