中央稳定板对分体箱梁桥梁的涡振控制
程 怡,周 锐,杨詠昕,葛耀君
(1.福州大学 阳光学院,福建 福州 350015;2.深圳大学 城市智慧交通与安全运维研究院,广东 深圳 518060;3.同济大学 土木工程防灾国家重点实验室,上海 200092)
当桥梁结构在风洞试验或者实桥运营中出现了颤振或大振幅涡振等现象不能满足抗风要求时,就需要采取有效的抗风控制措施来改善桥梁的整体抗风性能,使其满足抗风要求[1-2].桥梁结构的抗风控制措施主要分为气动措施、结构措施和机械措施.其中,气动措施是通过附加外部装置或修改结构的截面外形,改善其周围的绕流状态,从而提高抗风稳定性,减小风致振动的幅度,由于这种方法可靠性好,对结构改变相对较小,经济代价较低,因此是一种很实用的控制方法[3].常见的气动控制措施主要有两大类:① 采用中央开槽、竖向稳定板和导流板等措施;② 对主梁附属装置如栏杆、检修车轨道等的位置和形状做适当调整[4-5].现有的几座大跨度桥梁针对可能的风致振动问题,都采取了气动措施来改善桥梁的抗风性能,例如,舟山西堠门大桥采用了分体双箱梁,香港青马大桥和润扬长江大桥采用了中央稳定板,明石海峡大桥采用了加稳定板形式的桁梁等.
当一种气动控制措施的控制效果还不能完全达到预期控制目标时,可以尝试两种或更多措施的组合控制[6].例如,昂船洲大桥和嘉绍大桥的中央开槽和梁底导流板的组合时的风洞试验结果表明,当两者共同作用时有良好效果,可消除各个攻角下主梁的涡激共振[7-8];对于开口断面只有同时采用稳定板和扰流板才能有效地将涡振振幅控制在规范的允许值内[9];抑流板对于半开口分体箱梁的涡振控制效果要优于水平翼板[10];针对闭口箱梁的中央开槽和中央稳定板组合颤振控制效果研究表明,在中央开槽措施基础上,组合稳定板措施能进一步提升颤振控制效果[11].目前多种气动措施的组合都是基于经验来判断和不断尝试,将这些气动措施应用到实际桥梁结构前,都要经过风洞试验或数值模拟,来验证其控制效果.
虽然被动气动措施是目前最常用的桥梁气动措施,但在找到有效的颤振(或涡振)控制措施后,还必须重新检验施加措施后结构的其他风振性能,如涡振(或颤振)、抖振、风致静力稳定性和风荷载等[12].而且,控制措施具有很强的气动敏感性,同一种控制措施的尺寸和位置不同时的作用效果差异很大[13].例如,不同开槽率下分体箱梁的颤振稳定性能不同,不同高度的竖向稳定板对闭口箱梁的颤振控制效果也不同.研究发现,不同高度的中央稳定板和中央开槽组合措施下的颤振控制效果明显不同[14].然而,目前还没有人针对中央稳定板和中央开槽这种组合措施下的涡振控制效果进行校验.为了系统地研究中央开槽和中央稳定板组合措施的涡激共振控制效果,本文以常用的20%开槽率的分体箱梁桥梁为背景,首先,利用节段模型风洞试验,研究了6种典型高度的上中央稳定板(UVCS)和下中央稳定板(DVCS)作用时,分体箱梁的竖向涡振和扭转涡振发生的锁定风速区间和峰值响应;然后,通过计算流体动力学(CFD)分别对这些中央稳定板作用下分体箱梁的涡振控制效果和机理进行了对比研究,并比选出最佳的控制方法.该研究对于合理选择气动措施来改善分体箱梁桥梁的整体抗风性能具有重要的意义.
1 涡振控制试验
1.1 节段模型试验
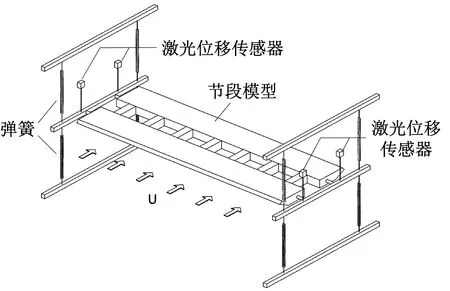
以主跨1 650 m的西堠门大桥为工程背景,选取了1∶60几何缩尺比,不考虑栏杆等附属结构,设计了6个具有代表性的上、下中央稳定板:稳定板相对高度h/H(h为稳定板高度,H为主梁高度)取0、0.2、0.4、0.6、0.8和1.0.节段模型的具体参数和实桥断面尺寸分别如表1和图1所示.节段模型长为1.74 m.为了研究加稳定板后气动外形改变对桥梁气动性能的影响,假设结构参数不变.采用弹簧悬挂二元刚体节段模型,在同济大学TJ-1风洞开展涡振试验,在均匀流场中进行了+3°、0°和-3°三个风攻角的试验,节段模型涡振试验如图2所示.
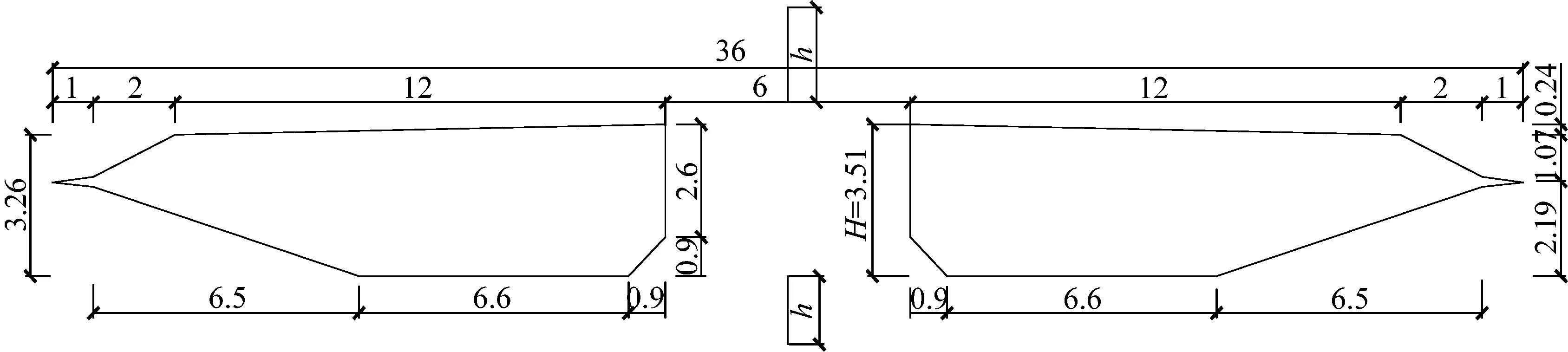
图1 带中央稳定板的分体箱梁断面图 (单位:m)Fig.1 Sectional model of twin-box girder with VCS (unit:m)

表1 带中央稳定板的分体箱梁桥梁的结构参数Tab.1 Structural parameters of twin-box girder with VCS
1.2 上稳定板的涡振响应
对比了+3°、0°和-3°三个风攻角下带不同上中央稳定板的分体箱梁的竖向涡振响应,发现+3°攻角是最不利攻角.图3描述了6种高度的上中央稳定板的竖向和扭转涡振位移响应的均方根(RMS)值.图3a表明,0.8h/H上中央稳定板的竖向涡振位移响应最大,约达到0.26 m;其次是1.0h/H和0.6h/H上稳定板,分别约为0.23 m和0.22 m;而
a 无中央稳定板

b 上中央稳定板

c 下中央稳定板
0.2h/H和0.4h/H上稳定板的竖向涡振响应却小于无稳定板的,分别约为0.14 m和0.13 m.此外,这6种工况都呈现2个锁定区间,带上中央稳定板后最大峰值对应的风速明显变小,特别是0.4h/H对应的折减风速Ur=U/fhB=6.5/(0.324×36)=0.56.因此,带上中央稳定板后分体箱梁桥梁的竖向涡振振幅峰值顺序从小到大依次为0.4h/H、0.2h/H、0、0.6h/H、1.0h/H、0.8h/H;加0.2h/H和0.4h/H上中央稳定板,有利于减小该分体箱梁桥梁的竖向涡振.图3b表明,0.6h/H和0.8h/H上中央稳定板的扭转涡振位移响应都很大,约0.3°,其次是1.0h/H和0.4h/H上稳定板,分别约为0.25°和0.20°,而0.2h/H上稳定板的竖向涡振响应却小于无稳定板的,仅为0.125°,且对应的锁定风速较大.其他5种工况的折减风速约为Ur=U/fvB=8/(0.232×36)=0.96.因此,带上中央稳定板后分体箱梁桥梁的扭转涡振振幅峰值顺序从小到大依次为0.2h/H、0、0.4h/H、1.0h/H、0.6h/H、0.8h/H;加0.2h/H上中央稳定板,有利于减小该分体箱梁桥梁的扭转涡振.因此,加0.2倍和0.4倍梁高上中央稳定板的竖向和扭转涡振性能是相对较好的.
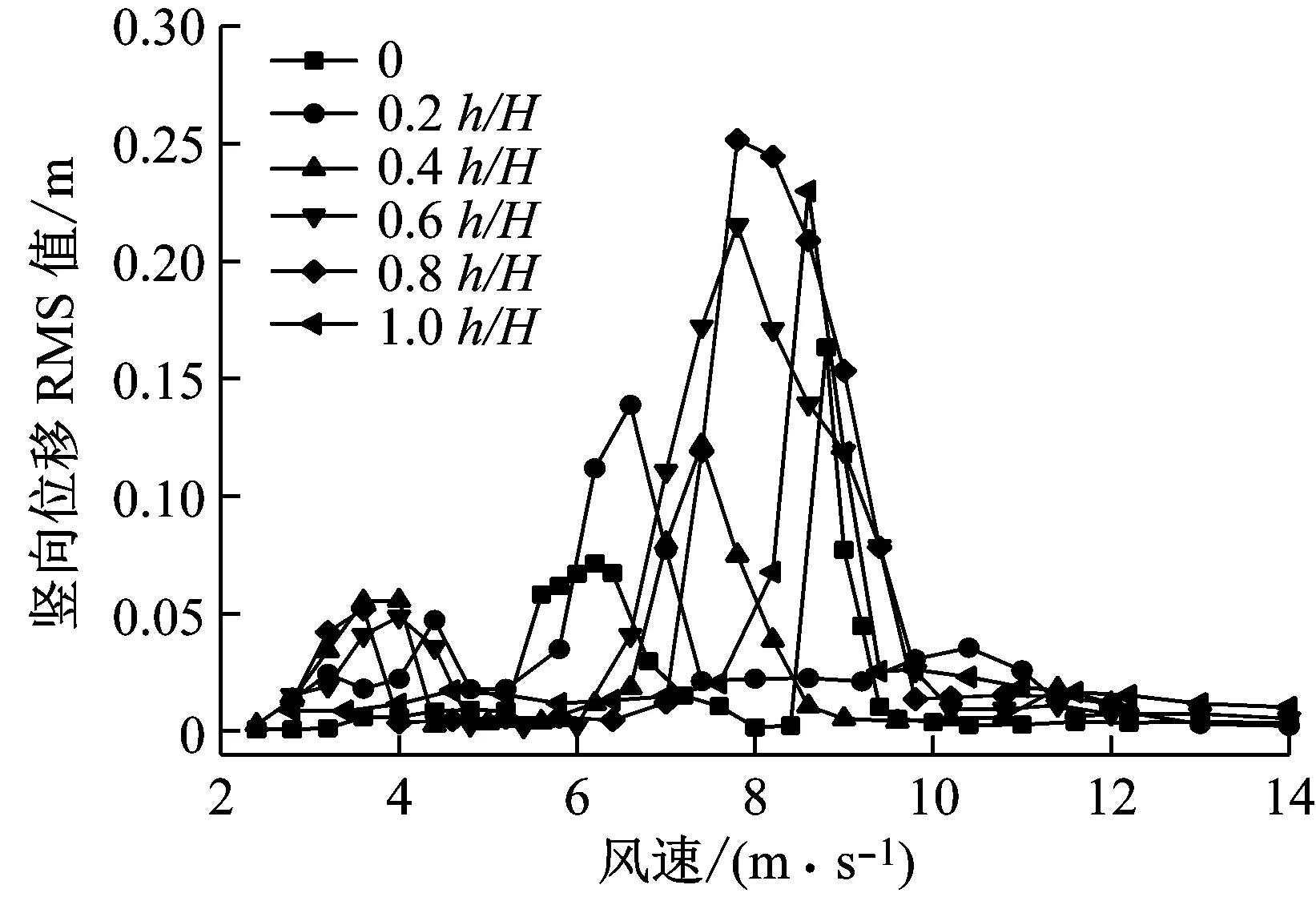
a 竖向
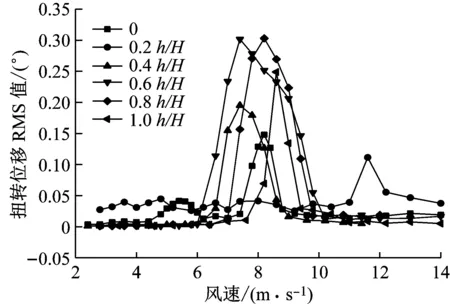
b 扭转
1.3 下稳定板的涡振响应
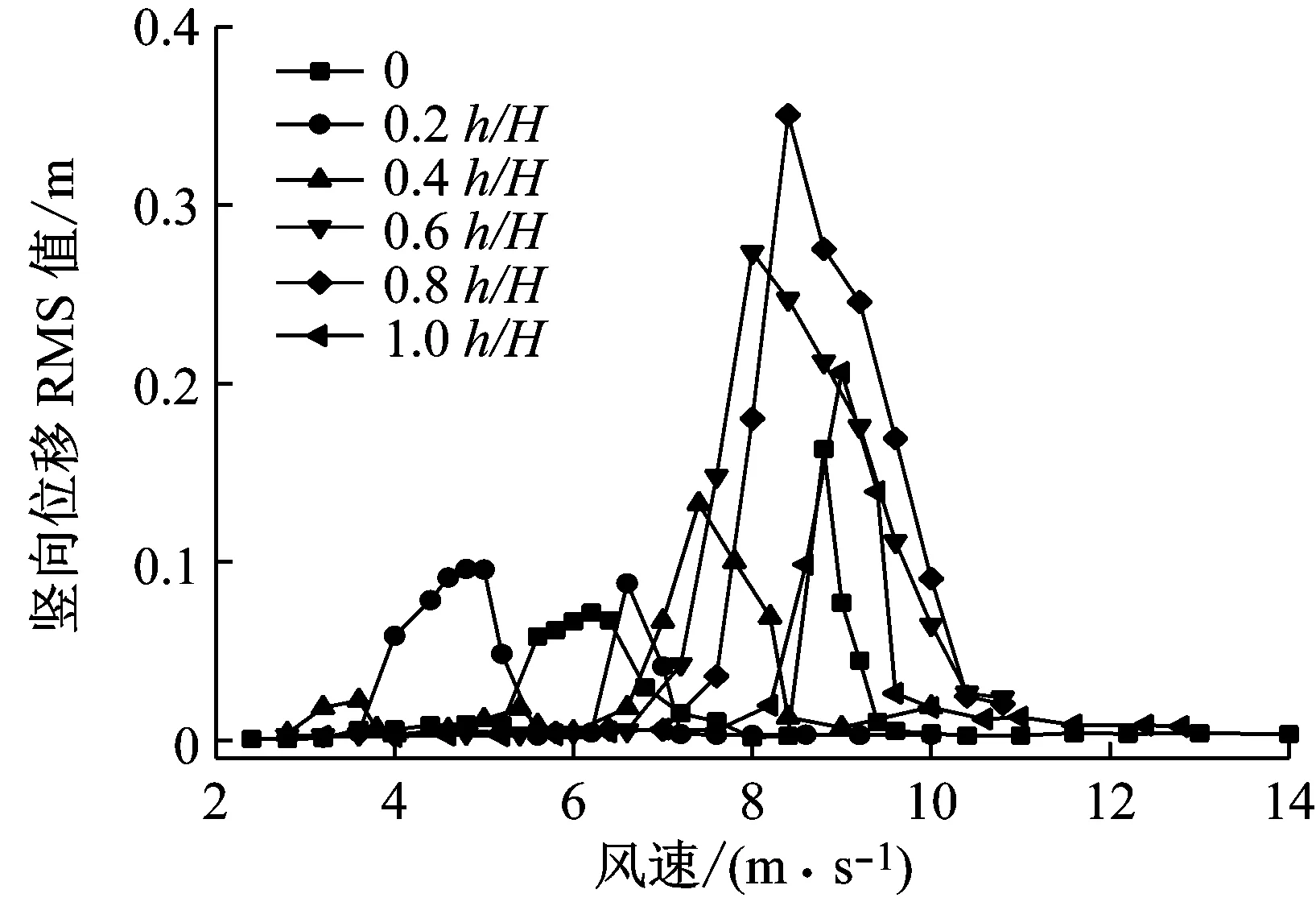
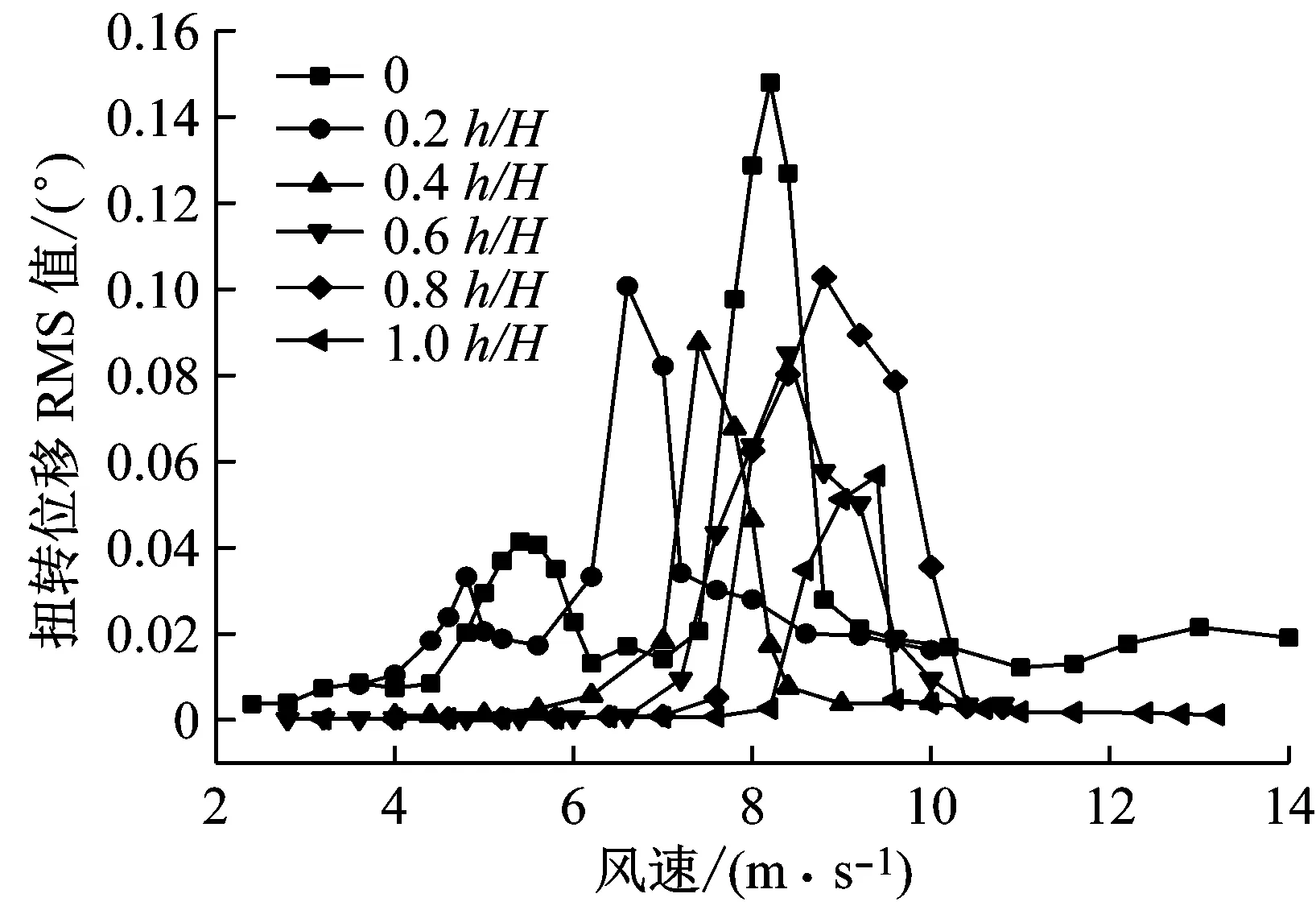
图4分别描述了6种高度的下中央稳定板的竖向和扭转涡振位移响应RMS值.图4a表明,0.8h/H的DVCS的竖向涡振位移响应也是最大,高达约0.36 m,其次是0.6h/H和1.0h/H的DVCS,分别约为0.28 m和0.21 m,而0.4h/H和0.2h/H的DVCS的竖向涡振响应也是小于无稳定板的,分别约为0.14 m和0.10 m.此外,带下中央稳定板后风速锁定期变为一个区间,最大峰值对应的风速也减小,特别是0.2h/H的稳定板.因此,带下中央稳定板后分体箱梁桥梁的竖向涡振振幅峰值顺序从小到大依次为0.2h/H、0.4h/H、0、1.0h/H、0.6h/H、0.8h/H;加0.2h/H和0.4h/H的DVCS有利于减小该分体箱梁桥梁的竖向涡振.图4b表明,加下中央稳定板后扭转涡振位移均明显减小,0.2h/H和0.8h/H的DVCS较大,其次是0.4h/H和0.6h/H的DVCS,最小的是1.0h/H高稳定板,仅为0.055°.此外,带下中央稳定板后风速锁定区间变为一个,0.2h/H的DVCS峰值对应的风速最小.因此,带下中央稳定板后分体箱梁桥梁的扭转涡振振幅峰值顺序从小到大依次为1.0h/H、0.6h/H、0.4h/H、0.2h/H、0.8h/H、0;加5种下稳定板都有利于减小该分体箱梁桥梁的扭转涡振.综合竖向和扭转响应的对比结果,加0.2h/H和0.4h/H的DVCS是加5种下稳定板中较好的,而0.8h/H下稳定板是最不利的;下中央稳定板的涡振控制效果相对好于上稳定板,特别是扭转涡振.因此,加0.2h/H下稳定板的涡振控制效果最好,其次分别是0.4h/H下中央稳定板和0.2h/H高上稳定板.
a 竖向
b 扭转
2 涡振控制数值模拟
由于中央稳定板会导致分体箱梁断面气流绕流流态特别是旋涡生成及其运动规律变得更为复杂,导致分体箱梁可能存在较大的涡激共振,利用CFD分别模拟了上中央稳定板和下中央稳定板作用时分体箱梁桥梁的涡振性能.
2.1 CFD数值模型
借助同济大学刘十一博士[15]自主研发的基于非结构化有限体积法二维CFD 数值模拟平台进行计算,选用基于Smagorinsky模型的大涡模拟(LES)方法,采用长方形计算区域,迎风侧边界采用速度入口,背风侧边界采用压力出口.为兼顾计算精度和计算效率,在主梁断面周边及较近的尾流区域采用密网格并设置边界层,在计算域的周边选用疏网格,中间区域进行合理过渡,动网格采用三角形非结构化网格.当风速为U=5 m·s-1时,雷诺数为Re=27 000.计算域尺寸为[-230,-270]×[230,270],主梁中心位于(0,0)点.底层网格三角形边长为0.04 m,当风速为U=5 m·s-1时,壁面率y+≈2.7.具体网格划分如图5所示,网格三角形数量为185 412,网格点数量为93 382,用于求解动网格的代理网格节点数量为1 249,采用5层多重网格层数.

a 0.4h/H高上中央稳定板

b 0.4h/H下中央稳定板
2.2 上稳定板的涡振控制效果
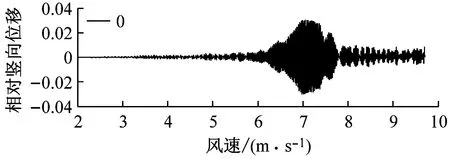
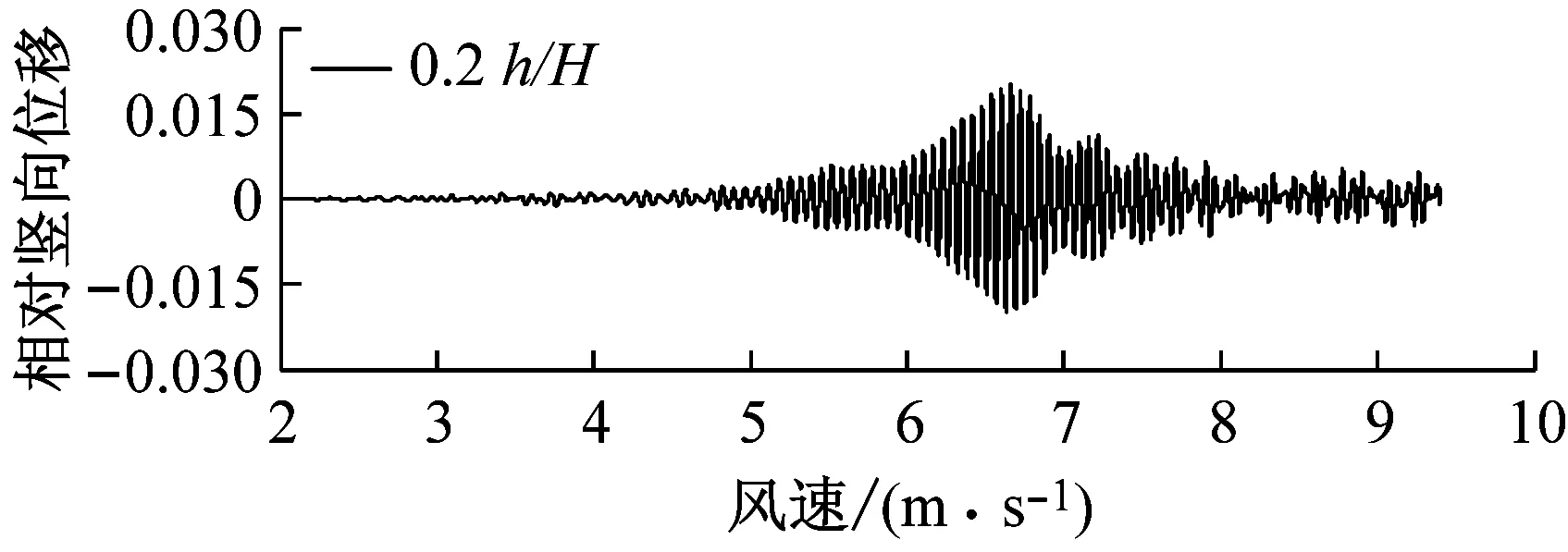
选取6种不同高度的上、下中央稳定板(相对主梁高度h/H为0、0.2、0.4、0.6、0.8、1.0),其他结构动力参数不变.图6对比了0°风攻角下不同高度上中央稳定板时分体箱梁的竖向和扭转涡振响应.对于竖向涡振响应,对于无稳定板在风速U=7.0 m·s-1时位移达到峰值,约为0.03倍梁高;0.2h/H上稳定板在风速U=6.6 m·s-1时位移达到峰值,约为0.02倍梁高;0.4h/H上稳定板在风速U=5 m·s-1时位移达到峰值,约为0.015倍梁高;0.6h/H上稳定板在风速U=5.6 m·s-1时位移达到峰值,约为0.05倍梁高;0.8h/H上稳定板在风速U=5.6 m·s-1时位移达到峰值,约为0.06倍梁高;1.0h/H上稳定板在风速U=7.6 m·s-1时位移达到峰值,大于0.06倍梁高.因此,竖向涡振振幅峰值的顺序从小到大依次为0.4h/H、0.2h/H、0、0.6h/H、0.8h/H、1.0h/H.对于扭转涡振响应,对于无稳定板在风速U=8.8 m·s-1时位移达到峰值,约为0.2°;0.2h/H上稳定板在风速U=8.8 m·s-1时位移达到峰值,大于0.2°;0.4h/H上稳定板在风速U=10.6 m·s-1时位移达到峰值,约为0.4°;0.6h/H上稳定板在风速U=10 m·s-1时位移达到峰值,约为0.35°;0.8h/H上稳定板在9.5 m·s-1之前没有出现扭转涡振;1.0h/H上稳定板在风速U=10 m·s-1时位移达到峰值,约为0.35°.因此,扭转涡振振幅峰值的顺序从小到大依次为0.2h/H、0、0.8h/H、0.6h/H、1.0h/H、0.4h/H.相对于扭转涡振,竖向涡振的问题更严重.图7显示了6种高度时上稳定板分体箱梁锁定风速区间中某个风速对应的涡振响应时程.

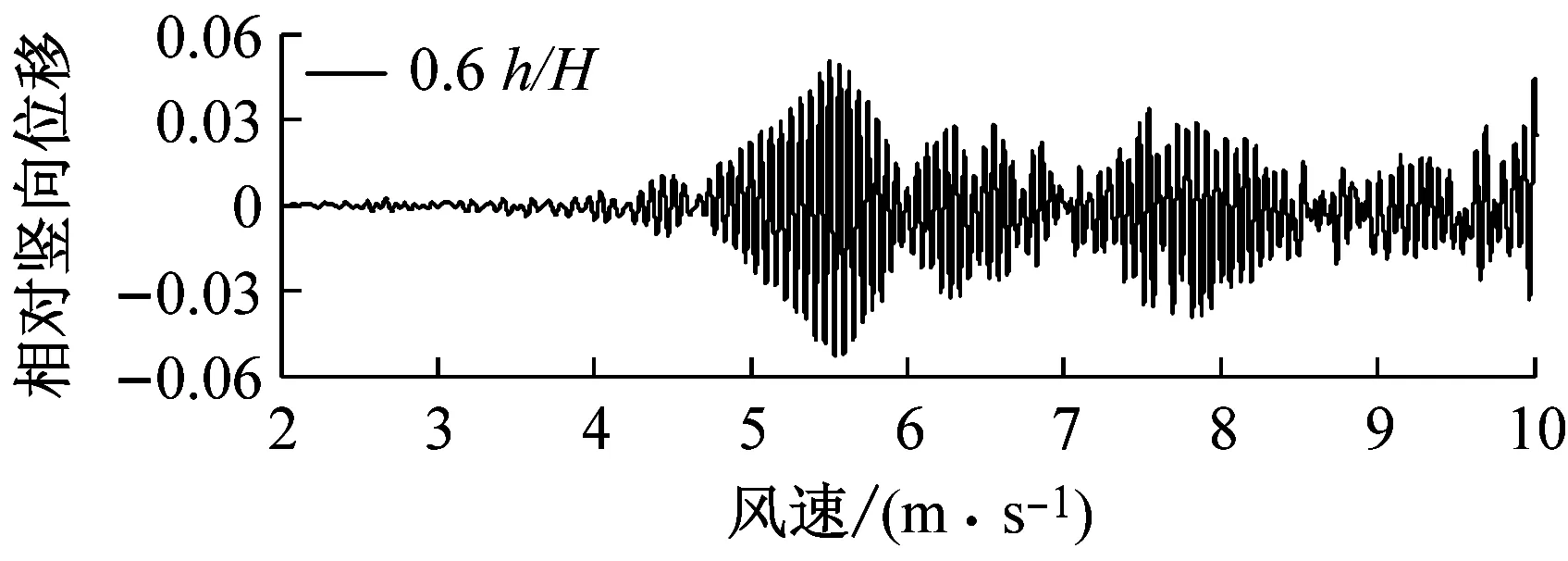
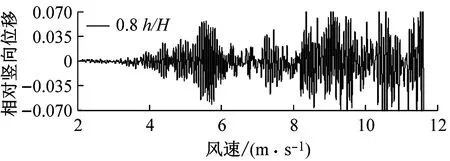
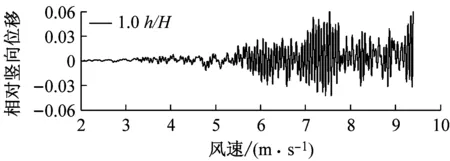
a 竖向
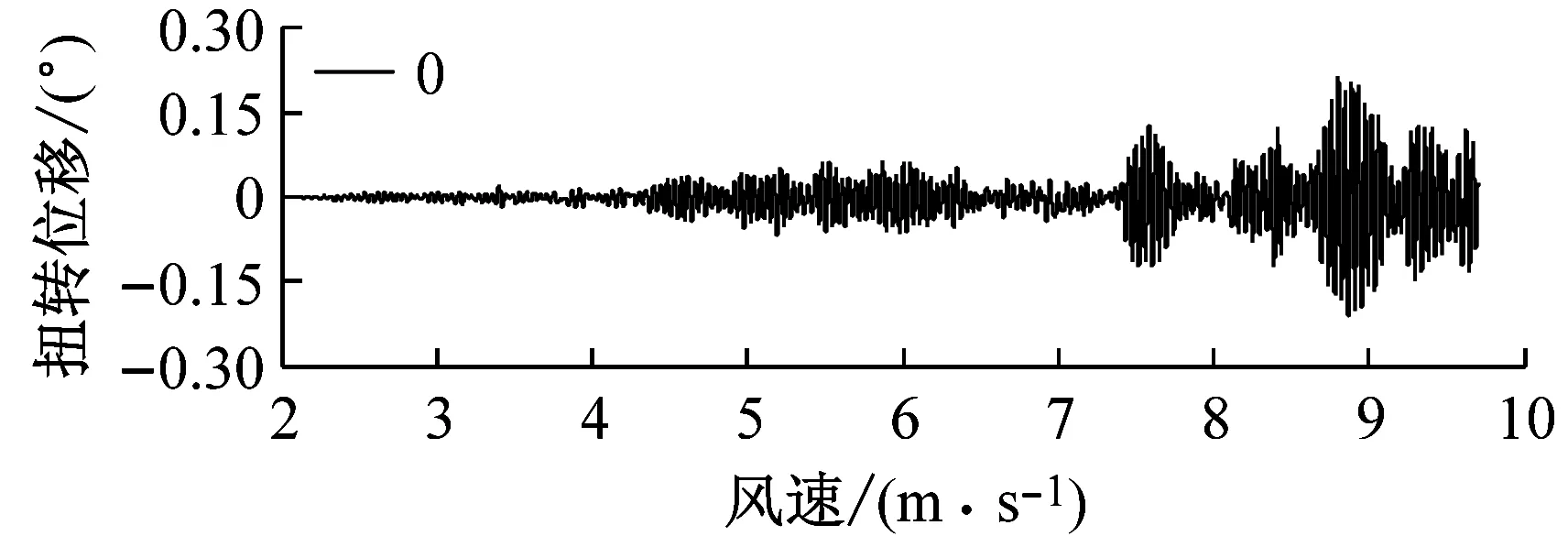

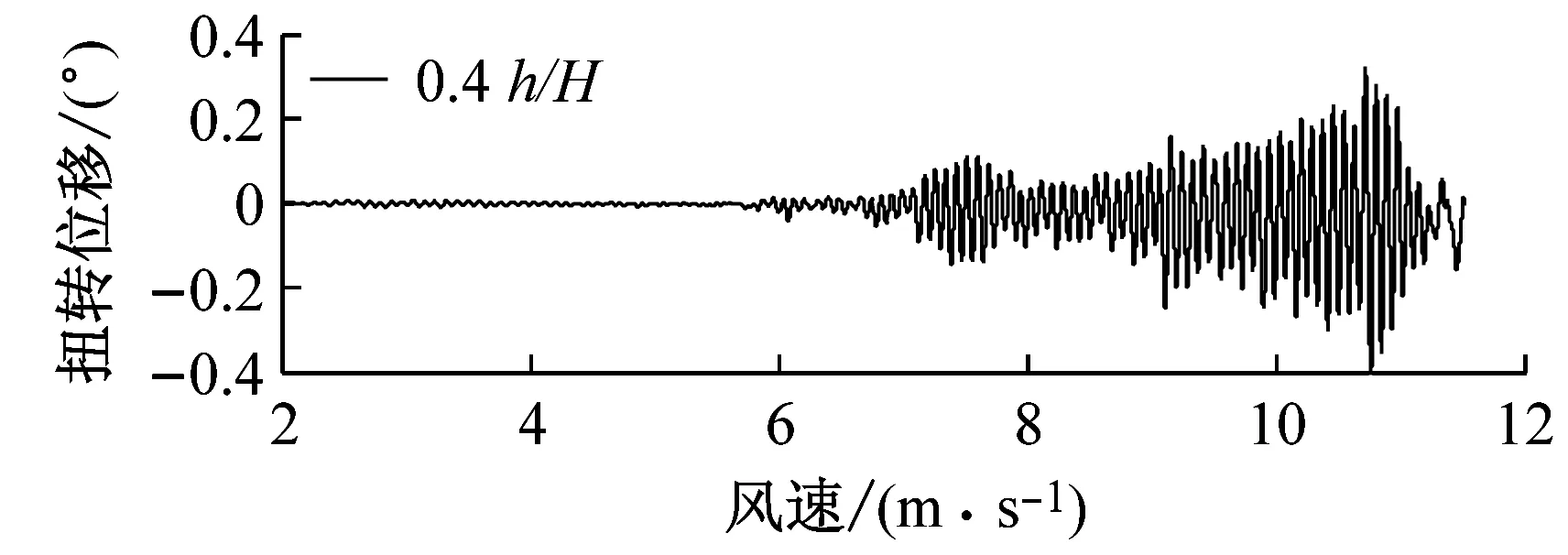
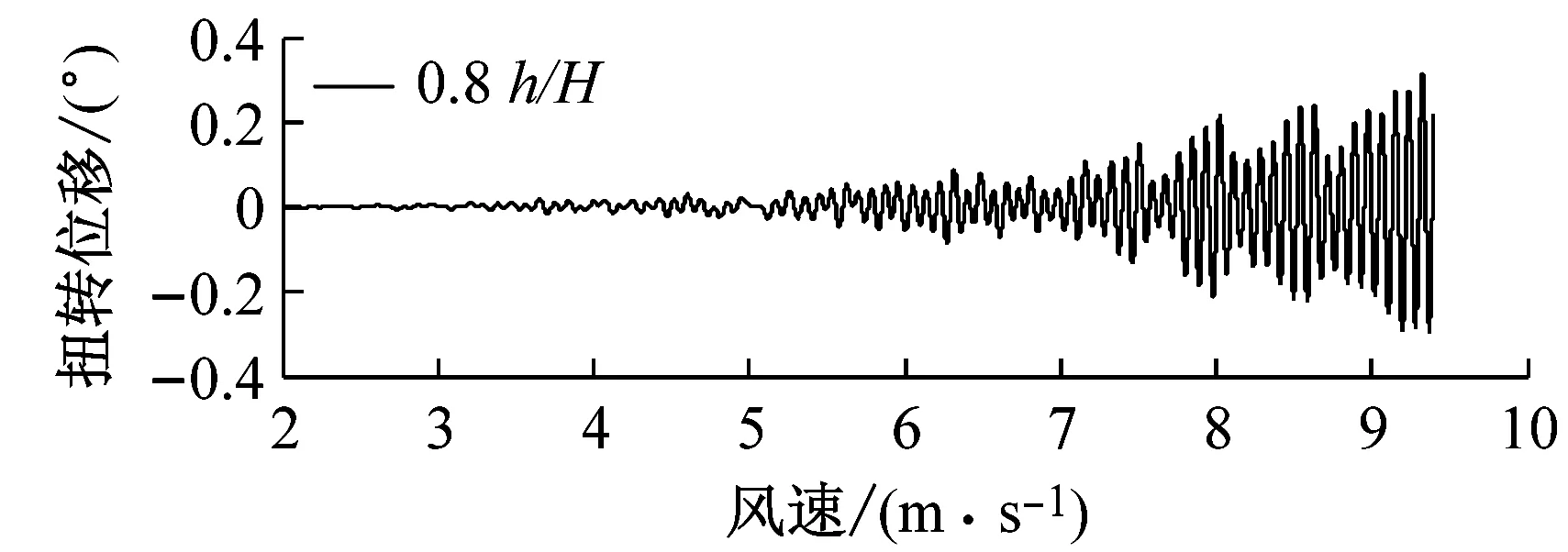
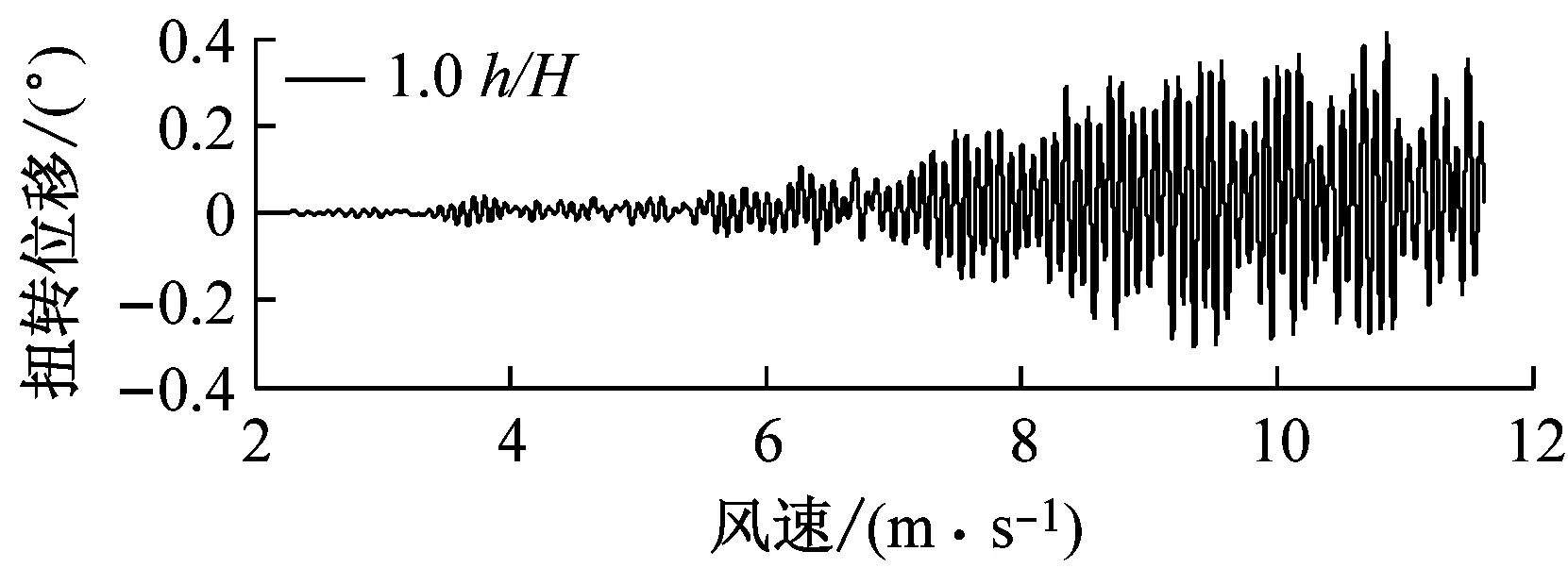
b 扭转
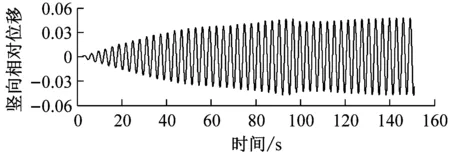
a 无中央稳定板,U=6.6 m·s-1
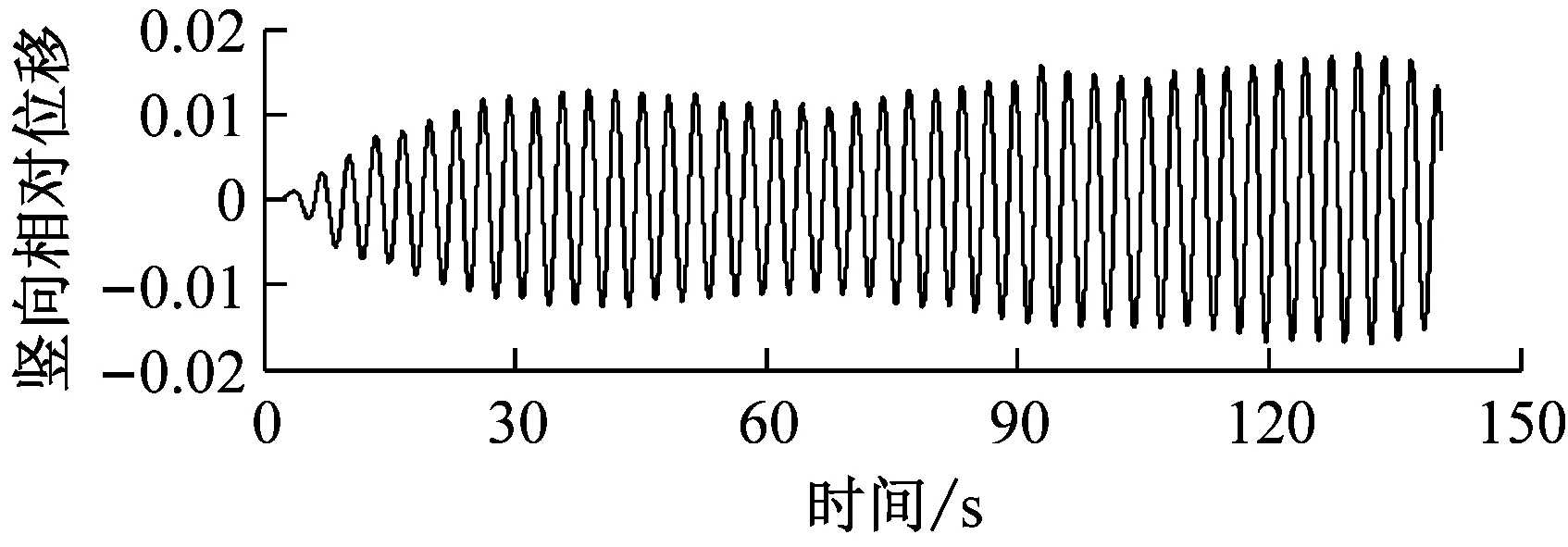
b 0.2h/H,U=6.5 m·s-1
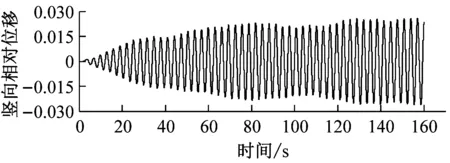
c 0.4h/H,U=5.1 m·s-1
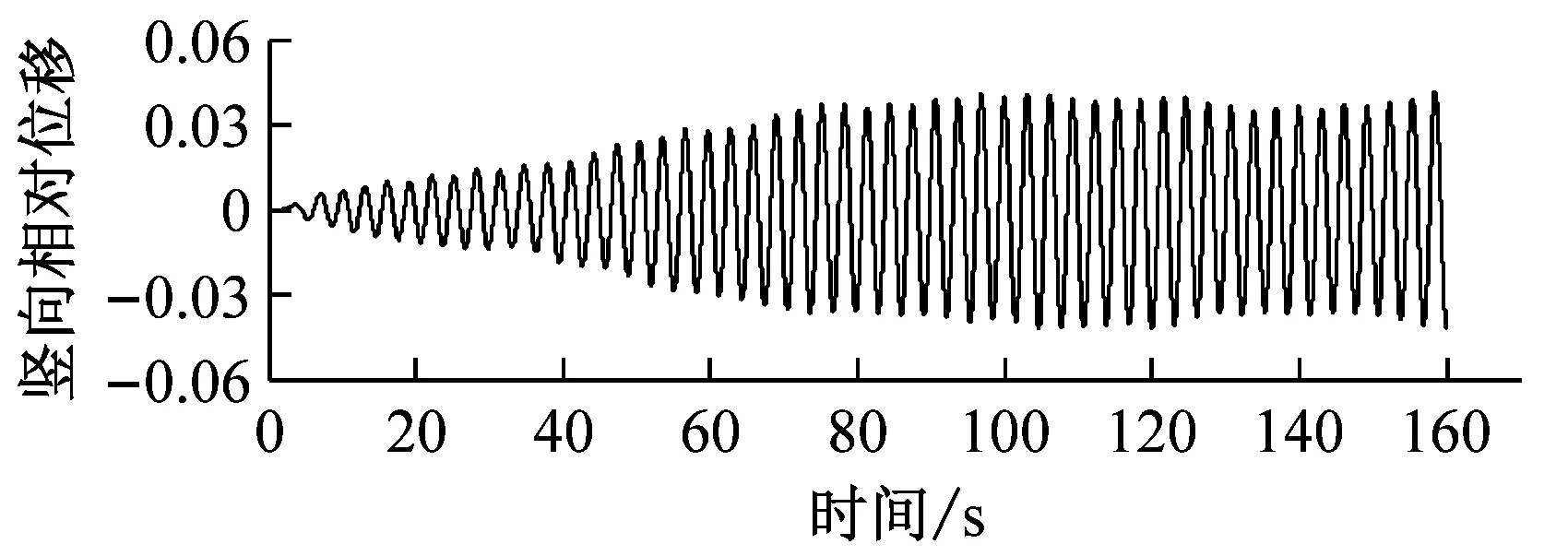
d 0.6h/H,U=5.4 m·s-1
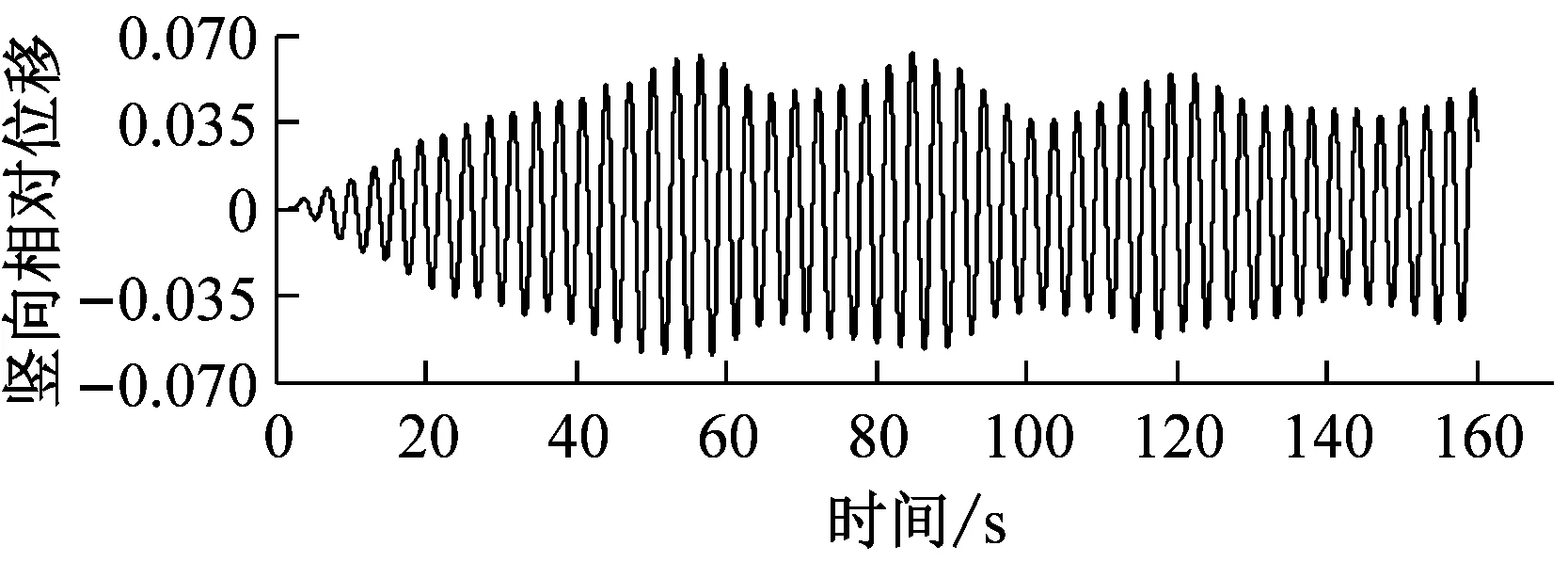
e 0.8h/H,U=5.8 m·s-1
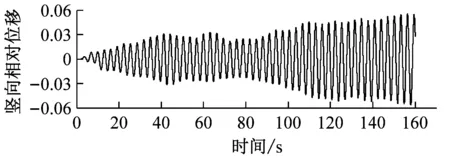
f 1.0h/H,U=6.1 m·s-1
2.3 下稳定板的涡振控制效果
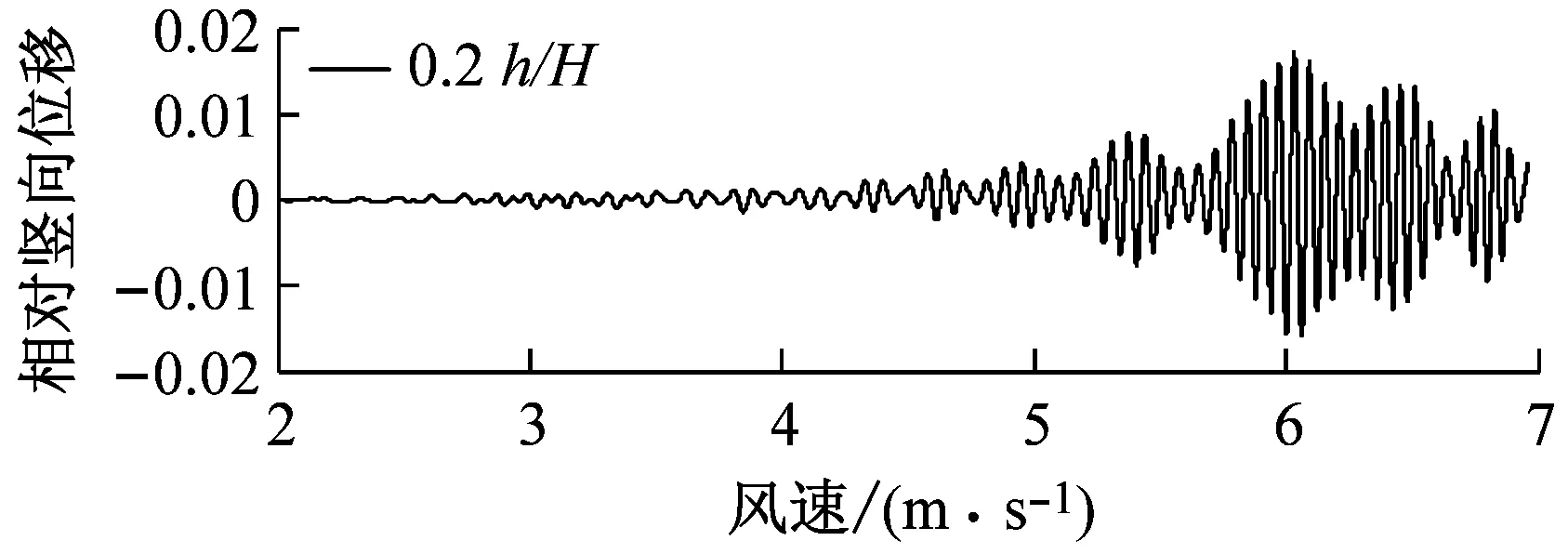
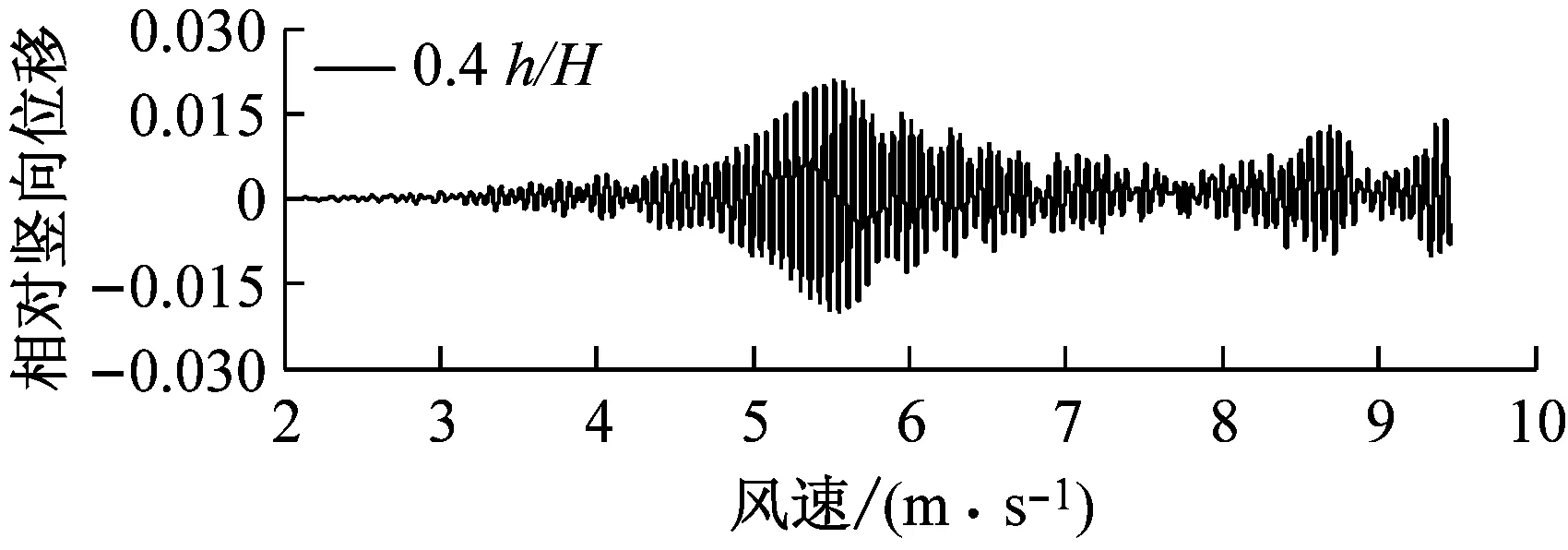
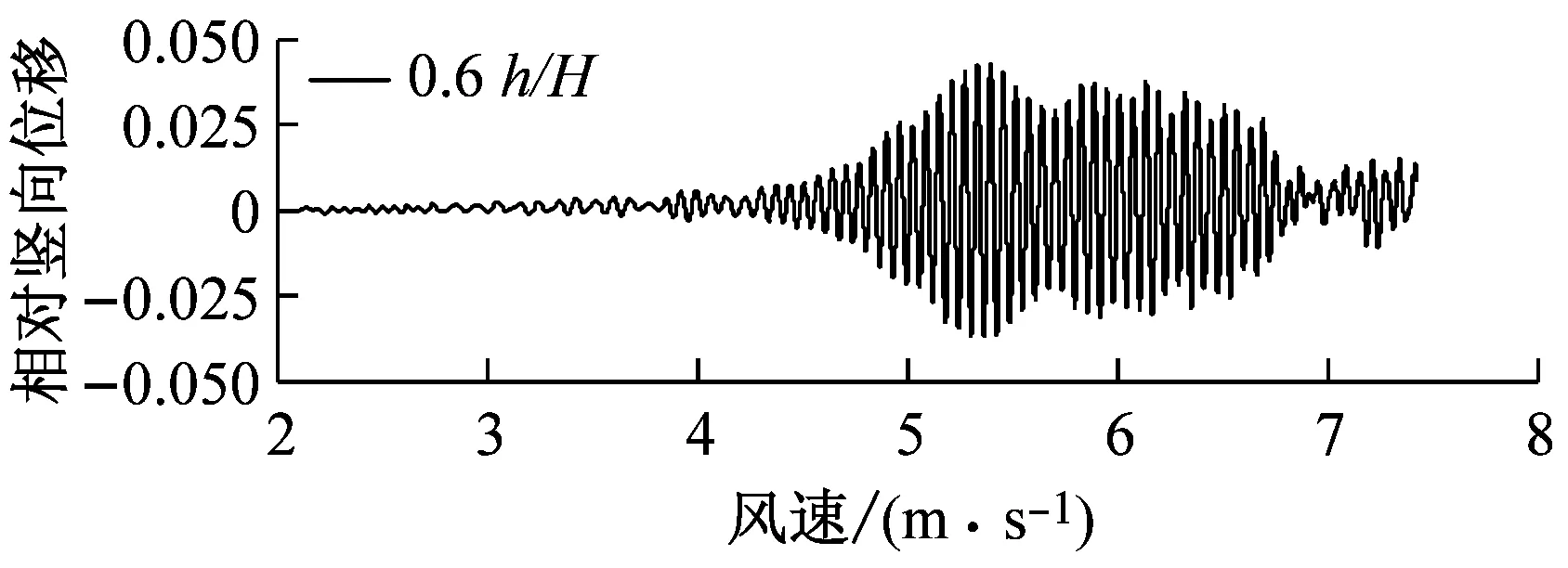
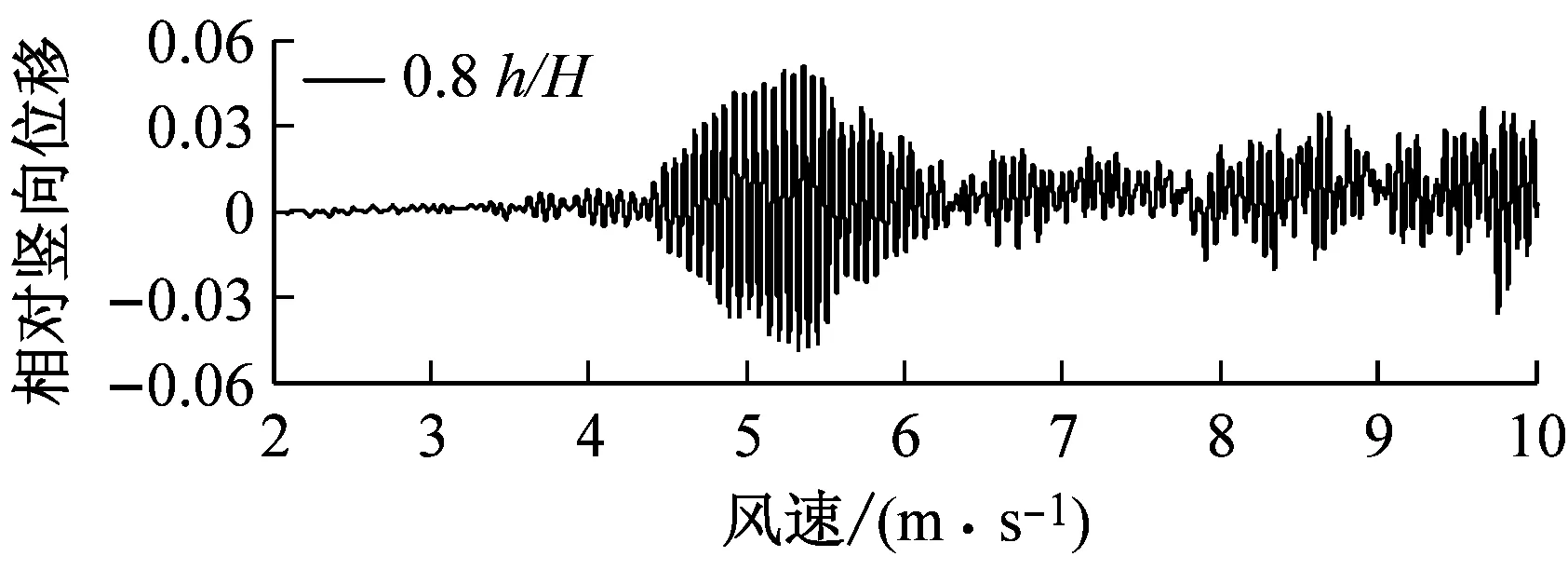
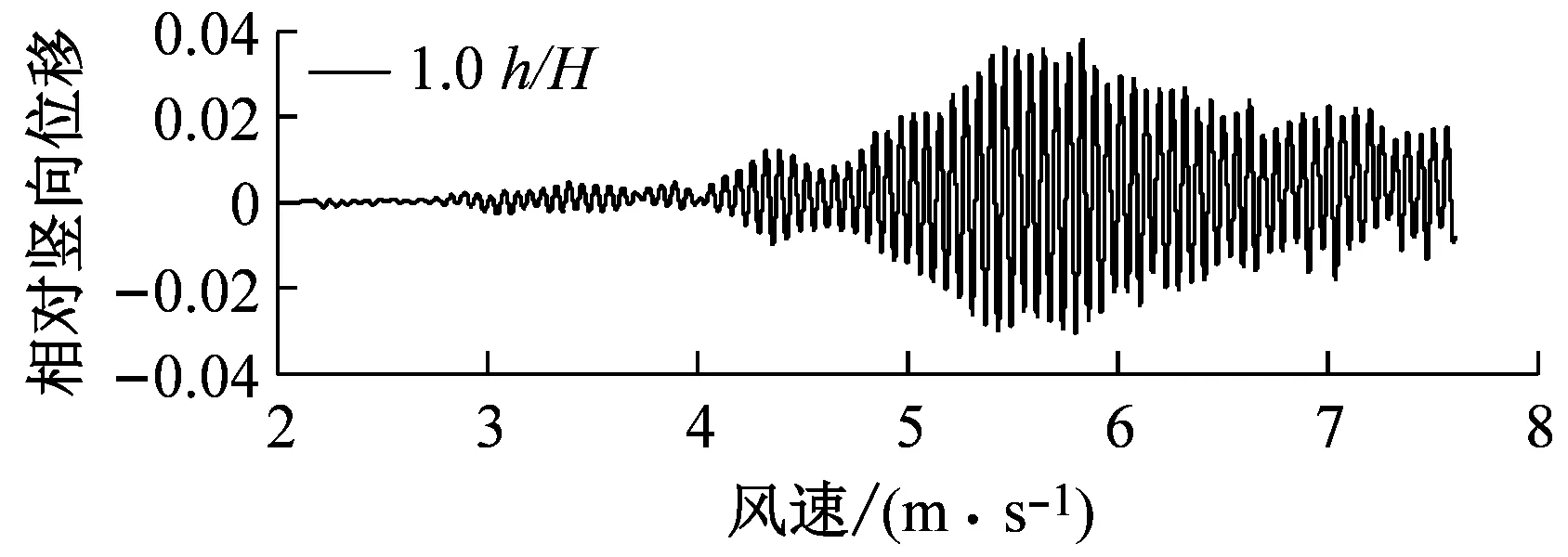
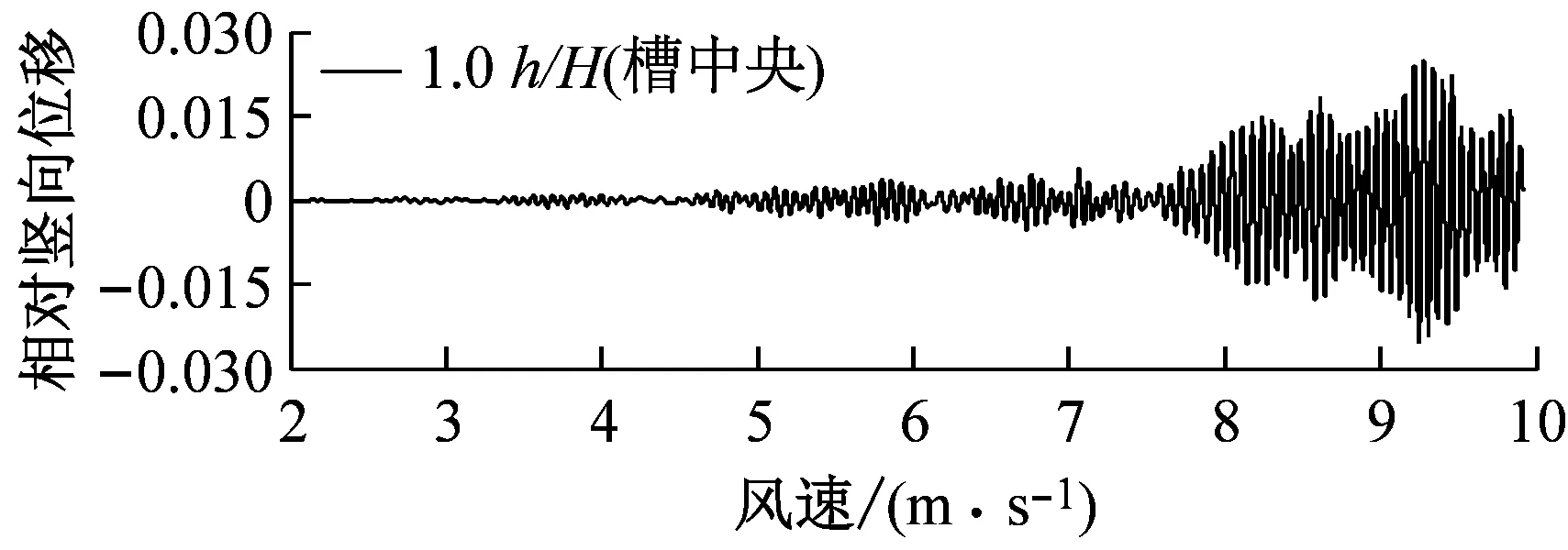
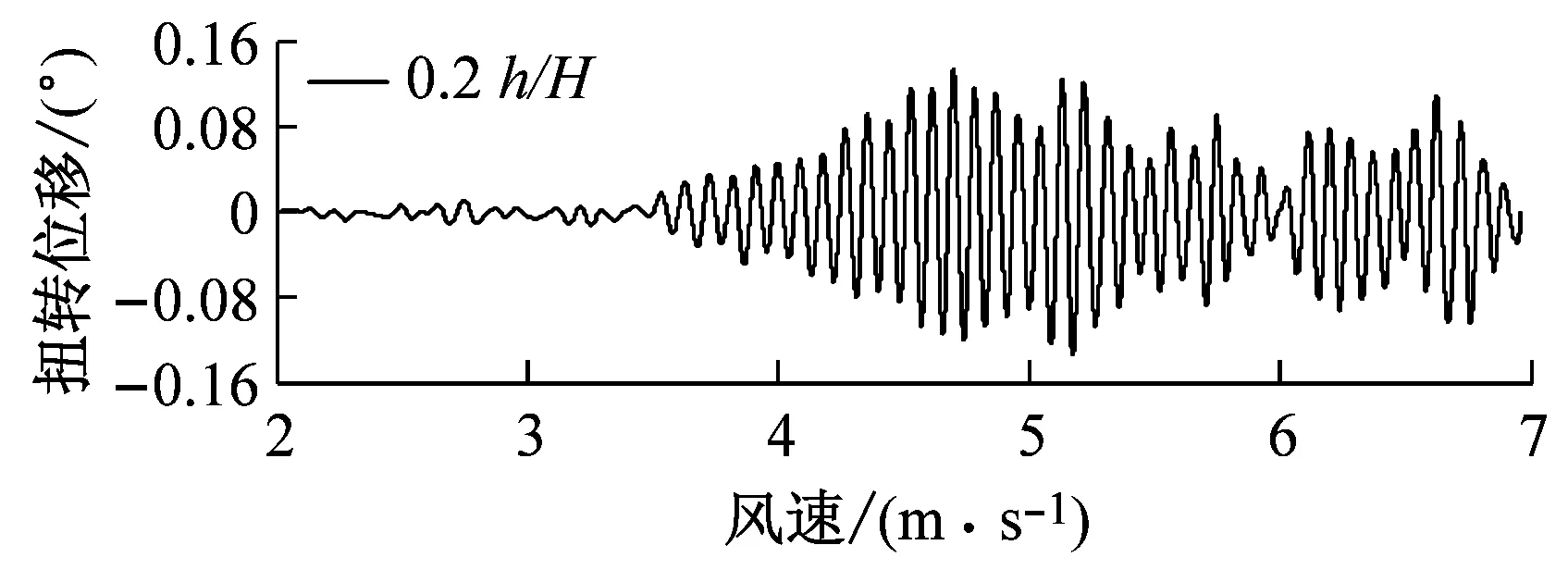
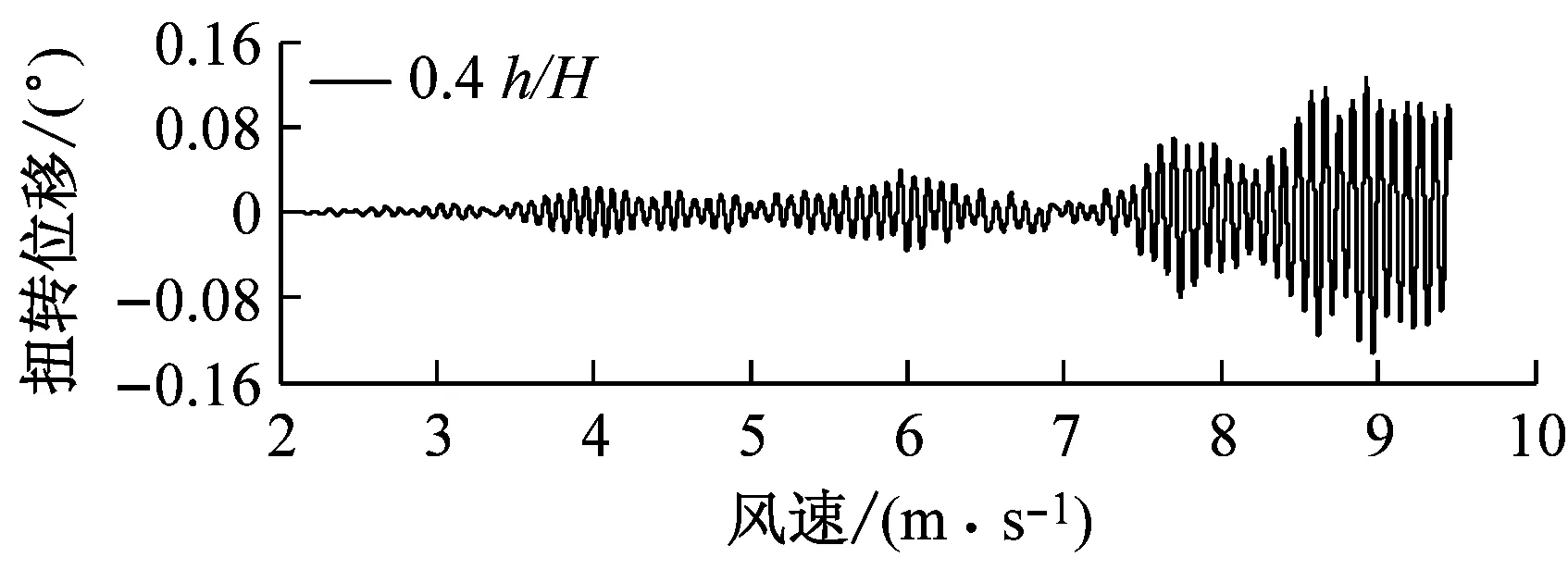
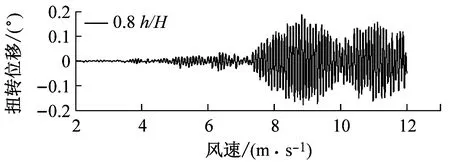
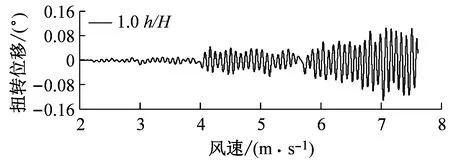
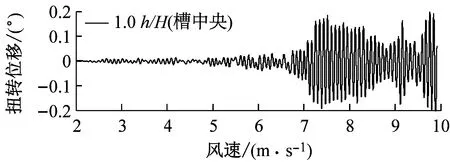
图8对比了0°风攻角、不同高度下中央稳定板和槽中稳定板(CVCS)时分体箱梁的竖向和扭转涡振响应.对于竖向涡振,0.2h/H的下稳定板在风速U=6.0 m·s-1时位移达到峰值,约为0.017倍梁高,低于无稳定板的;0.4h/H下稳定板在风速U=5.5 m·s-1时位移达到峰值,约为0.017倍梁高;0.6h/H下稳定板在风速U=5.2 m·s-1时位移达到峰值,约为0.04倍梁高;0.8h/H下稳定板在风速U=5.3 m·s-1时位移达到峰值,约为0.045倍梁高;1.0h/H下稳定板在风速U=5.4 m·s-1时位移达到峰值,约为0.036倍梁高;1.0h/H槽中稳定板在风速U=9.2 m·s-1时位移达到峰值,约为0.026倍梁高.因此,竖向涡振振幅峰值的顺序从小到大依次为0.2h/H、0.4h/H、0、1.0h/H、0.6h/H、0.8h/H.对于扭转涡振响应,0.2h/H下稳定板在风速U=4.6 m·s-1时位移达到峰值,约为0.13°;0.4h/H下稳定板在风速U=9.0 m·s-1时位移达到峰值,大于0.12°;0.6h/H下稳定板在风速U=6.4 m·s-1时位移达到峰值,约为0.1°;0.8h/H下稳定板在风速U=8.8 m·s-1时位移达到峰值,约为0.18°;1.0h/H下稳定板在U=7 m·s-1时位移达到峰值,约为0.15°;1.0h/H槽中稳定板在风速U=7.3 m·s-1时位移达到峰值,约为0.19°.因此,扭转涡振振幅峰值的顺序从小到大依次为0.6h/H、0.4h/H、0.2h/H、1.0h/H、0.8h/H、0.同样地,加下中央稳定板后竖向涡振相对于扭转涡振更严重,图9显示了6种高度时下稳定板分体箱梁锁定风速区间中某个风速对应的涡振响应时程.
3 涡振控制的机理
3.1 试验与CFD的结果对比
将二维CFD计算的结果和二维节段模型风洞试验结果进行对比,如图10所示.对于竖向涡振响应,CFD计算的结果接近于试验结果;随着稳定板高度的增加,竖向涡振位移先减后增,在高于0.4h/H稳定板时,下稳定板的位移响应比率要大于上稳定板的,且均大于1.对于扭转涡振响应,CFD计算的结果基本上接近于试验结果(在高上中央稳定板时稍微有些偏差);随着下稳定板高度的增加,下稳定板的扭转涡振位移比率逐渐减小,而上稳定板的位移先增后减,5种高度下稳定板的位移响应比率都小于1,而上稳定板的比率都大于1.
3.2 绕流形态的对比研究
分别对比了无稳定板、0.4h/H高上中央稳定板和0.4h/H高下中央稳定板作用下分体箱梁断面的涡度和压强图,如图11和图12所示.加了上、下中央稳定板后分体箱梁的绕流形态发生了明显的改变.图11a中在无稳定板时在分体箱梁的槽中形成了正负涡度的两个交替运动大漩涡,负涡度在背风侧梁的上表面再附着,而正涡度在背风侧梁的下斜腹板处也形成了大的漩涡,这样背风侧梁的上下表面就形成了明显的负正漩涡,从而产生较大的升力,并引起了激烈的竖向涡振运动.图12a的压强场也表明,在槽中有正负压区,在背风侧梁的上表面和下斜腹板处有明显的负压强,而下表面也是正压区,这样由槽中及背风侧梁形成的明显正负压强场引起了整个主梁的升力.
a 竖向

b 扭转
添加了上中央稳定板后,从图11b可以看到,在槽中的稳定板后端存在较大的负涡度漩涡,由于稳定板的存在,使得背风侧梁上表面的漩涡再附位置更远,接近于风嘴的上端,与此同时,背风侧梁的下表面没有明显的正涡度漩涡.图12b显示,在槽中的稳定板前端有明显的正负压强,而在稳定板后端只有较明显的负压,而且背风侧梁只有上表面有较明显的负压.即正负压强相互作用更加集中于下游位置并接近于风嘴处,这样导致相对原断面更小的竖向力,因此竖向涡振运动没有那么明显.添加了下中央稳定板后,图11c显示,在槽中的稳定板后端存在较大的交替的正负涡度漩涡,由于稳定板的存在,使得背风侧梁下表面存在较大正涡度的漩涡,上表面斜腹板靠近风嘴处才有较大的负涡度的漩涡.图12c显示,在槽中的稳定板前端是明显的正压强区,而后端有明显的负压强区,而且背风侧梁上、下表面均有较明显的负压.即正负压强相互作用更加集中接近于槽中位置,这样导致相对原断面更大的竖向力,因此竖向涡振运动没有那么激烈.
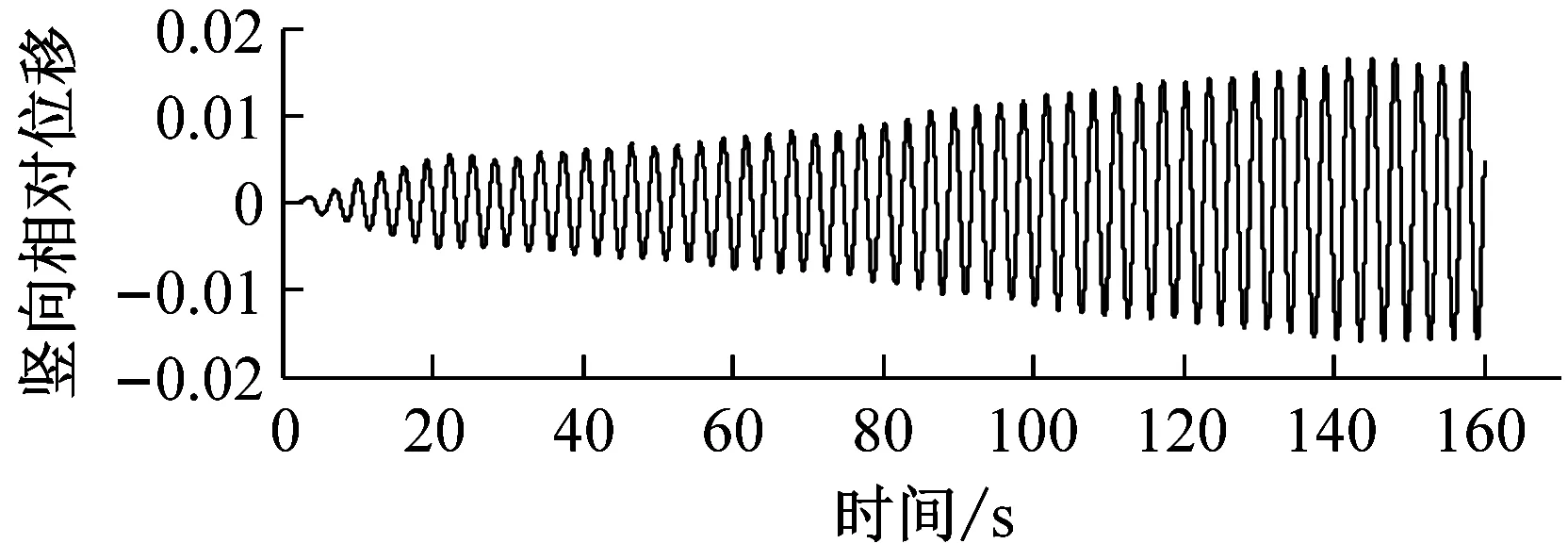
a 0.2 h/H,U=5.9 m·s-1
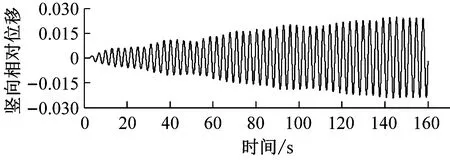
b 0.4 h/H,U=5.3 m·s-1
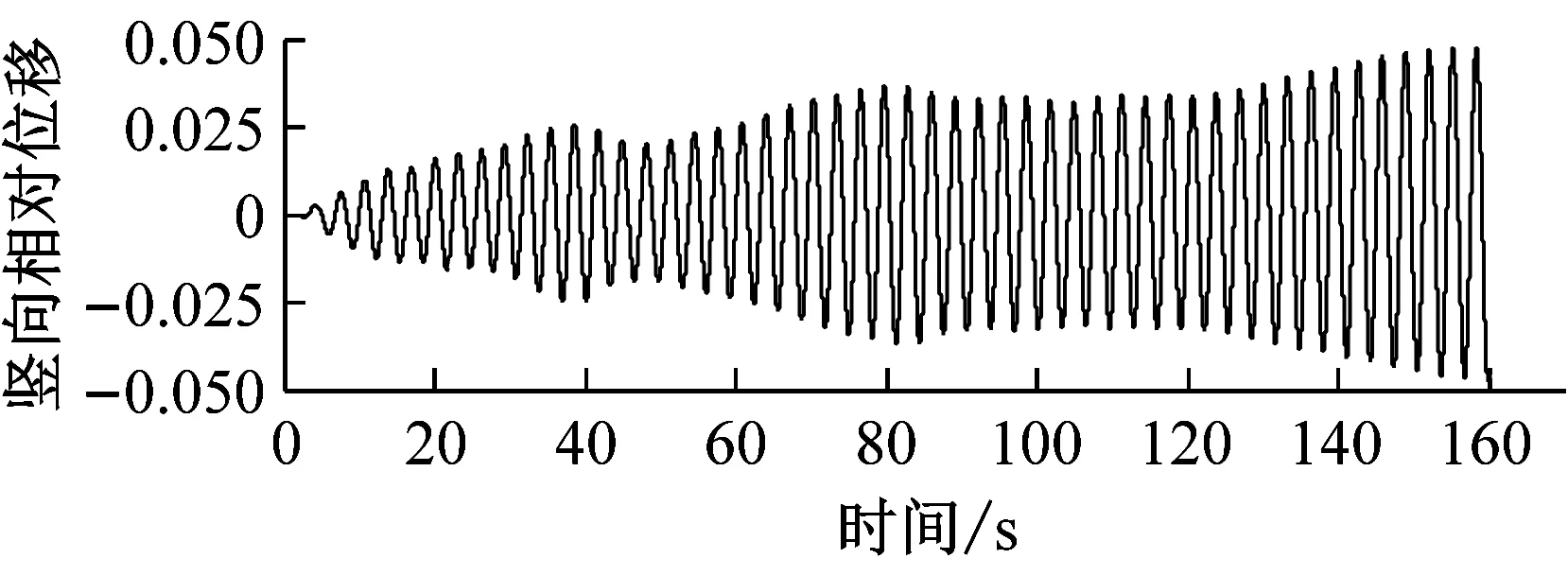
c 0.6 h/H,U=5.2 m·s-1
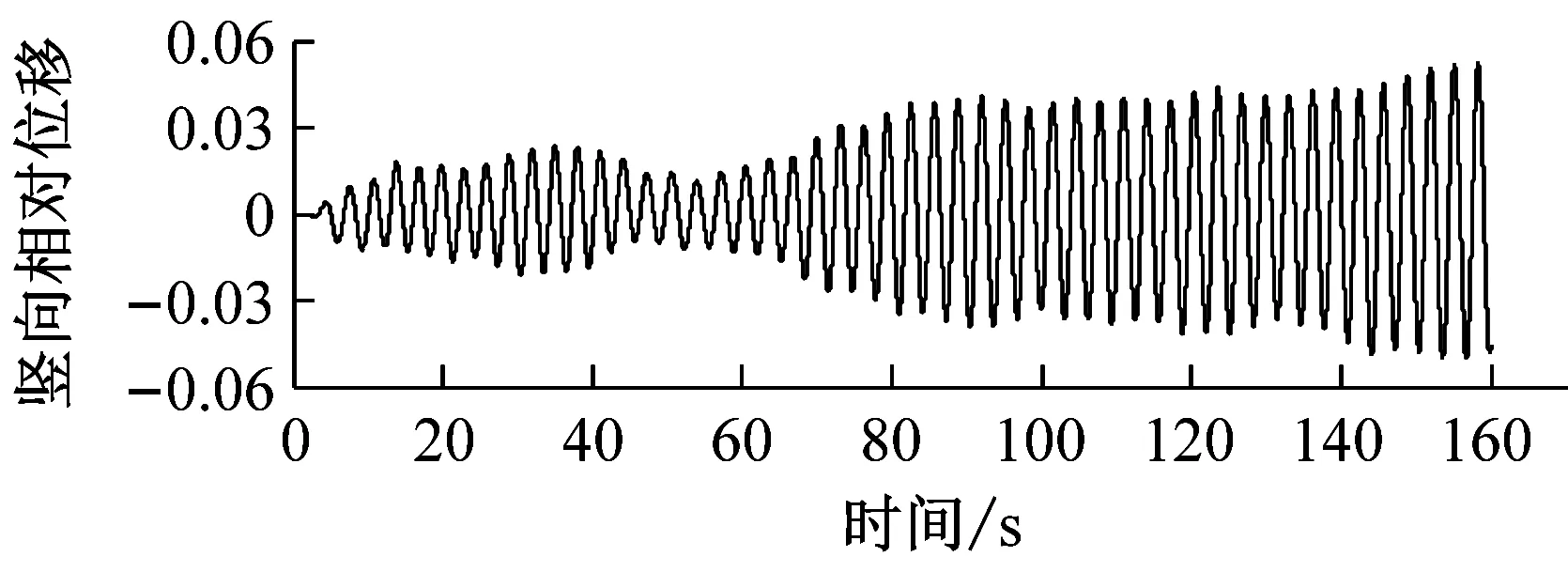
d 0.8 h/H,U=5.2 m·s-1
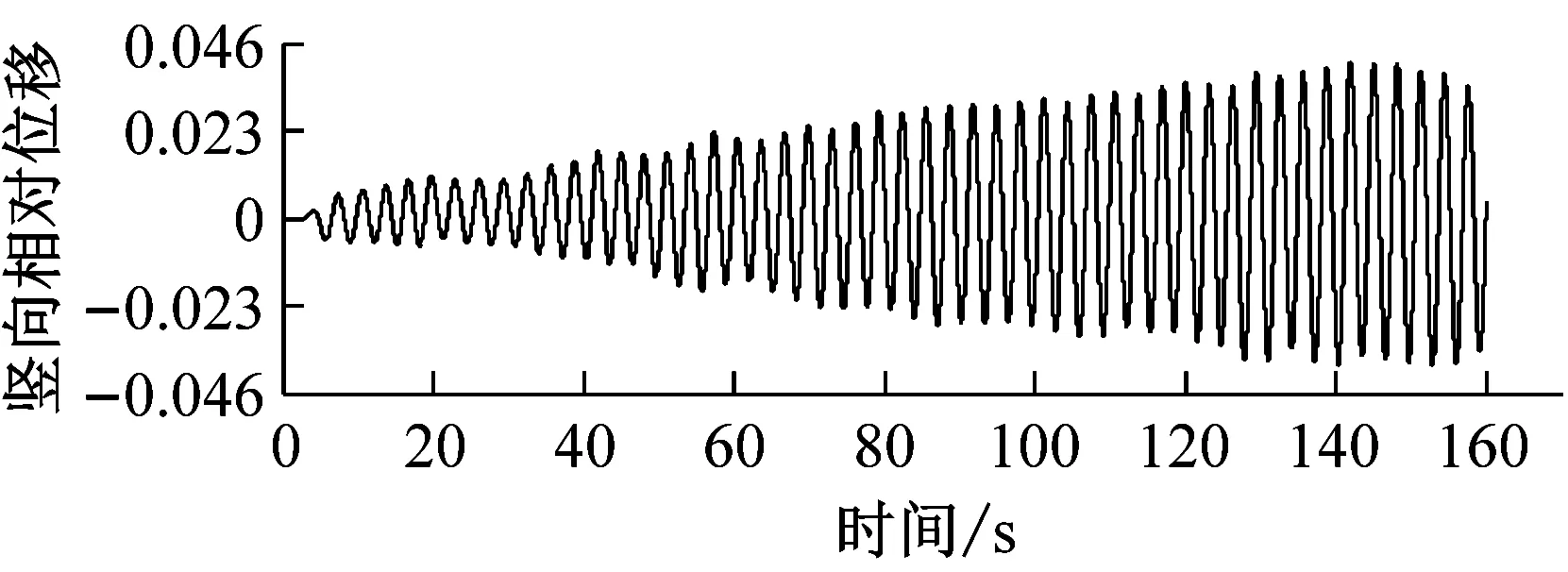
e 1.0 h/H,U=5.8 m·s-1
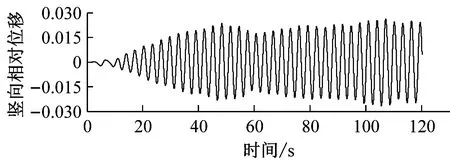
f 1.0 h/H(糟中央),U=9.1 m·s-1
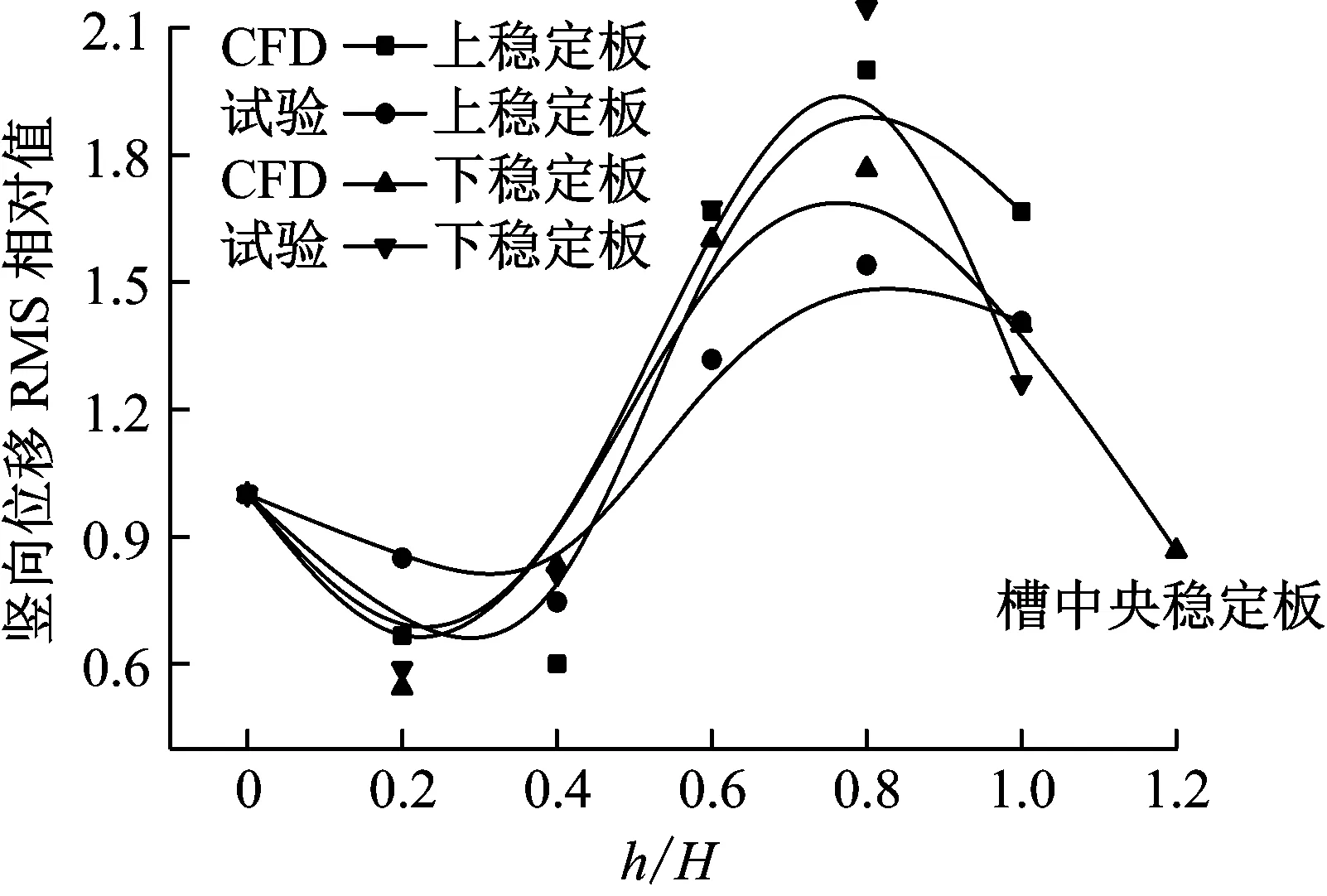
a 竖向

b 扭转

a 无稳定板

b 0.4h/H高上中央稳定板
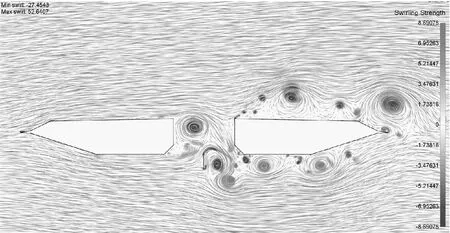
c 0.4h/H高下中央稳定板
因此,上、下中央稳定板的存在明显改变了槽中漩涡的运动方式和能量分布位置,以及背风侧梁上下表面的压强场.其中,上稳定板使得背风侧梁上表面的负涡度漩涡更靠近风嘴,而下稳定板使得背风侧梁下表面有了更多的正涡度漩涡.
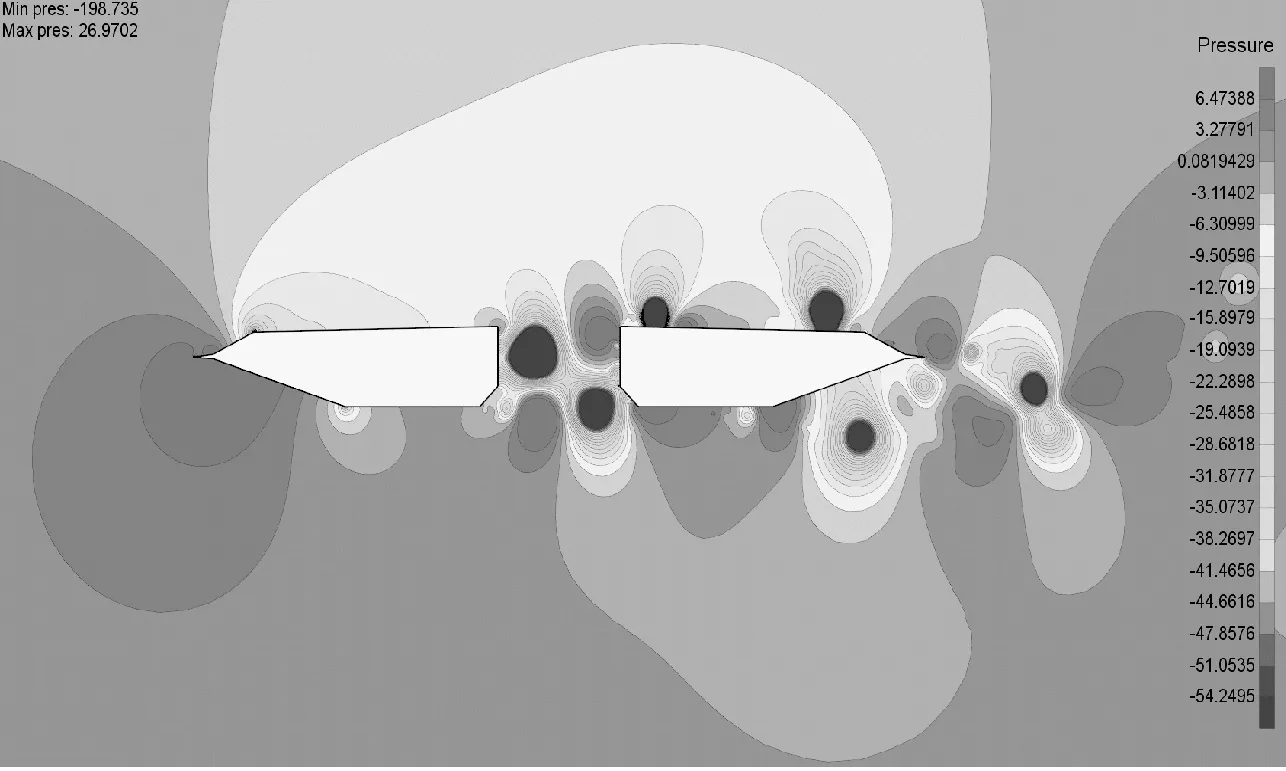
a 无稳定板
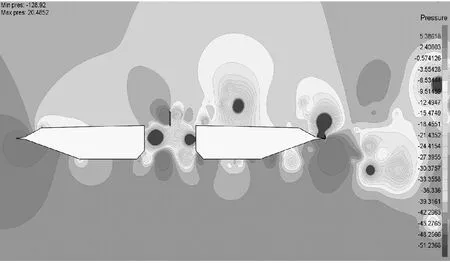
b 0.4h/H高上中央稳定板
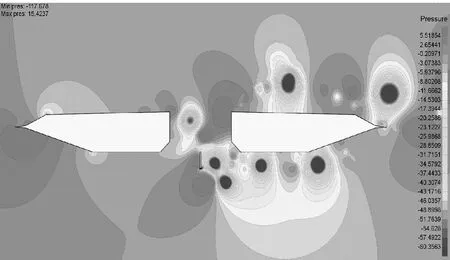
c 0.4h/H高下中央稳定板
4 结论
通过对不同高度和位置的中央稳定板对大跨度分体箱梁桥梁涡激共振控制效果的研究,可以得到以下主要结论:
(1)随着上稳定板高度的增加,涡振性能是先变好再变差,分别在0.4倍梁高时竖向涡振性能和0.2倍梁高时扭转涡振性能最好.
(2)随着下稳定板高度的增加,竖向涡振性能也是先变好再变差,而扭转涡振性能逐渐变好,分别在0.2倍梁高时竖向涡振性能和1.0倍梁高时扭转涡振性能最好.
(3)CFD计算的结果总体上接近试验结果,说明该数值模拟的结果比较可靠,绕流形态对比表明上、下中央稳定板通过改变槽中漩涡的运动方式和下风侧两端上下表面的压强,从而影响到升力大小和竖向涡振的振幅.
(4)综合对比,0.2倍梁高下稳定板的涡振控制效果最好,而0.8倍梁高上稳定板的涡振控制效果最不利.

