高效单旋式换热器入口分布器气液混合数值研究
胡兴苗 张贤安 胡霄乐 李军杰
镇海石化建安工程有限公司 (浙江宁波 315207)
对于高效单旋式换热器,在特定工况下,气液两相介质并未在管道中混合,而是分别从不同管口进入设备;在流体进入换热管前,需设置合理的入口分布器,使两相流得以均匀混合。气液两相混合均匀与否会在很大程度上影响换热管内流体的分配,如因混合不均匀出现偏流现象,会降低设备的换热效率。
目前,国内外对该类型分布器的研究较少。采用实验方法对工程实践的设备入口分布器内两相流体的分布情况进行研究,不仅存在一定的危险性与缺陷,还将耗费大量的时间和成本。本研究基于计算流体动力学(CFD)仿真技术,针对高效单旋式换热器的一种入口分布器结构进行了数值模拟。通过流场分析,可较为全面地获取入口分布器内气液两相的流动与混合状态,并为后续设备结构优化和产品升级提供一定的指导。
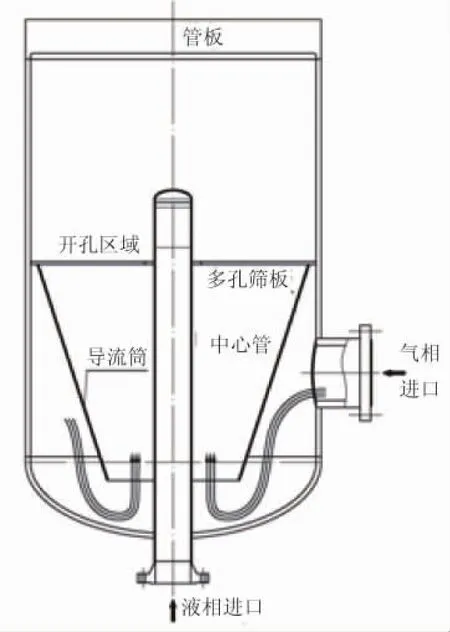
图1 入口分布器计算模型
1 理论基础与模型建立
1.1 模型建立与网格划分
入口分布器主要由导流筒、多孔筛板及中心管等结构组成,如图1所示。
气相由入口进入,流经导流筒后,从多孔筛板进入混合区域;液体则由中心管进入,流经开孔区域,喷入混合区域。气液两相在混合区域混合均匀后进入管板换热管中,其气液两相物性数据详见表1。

表1 气液两相物性数据及入口流量
基于ANSYS Workbench平台,建立入口分布器的几何模型,并对其进行网格划分,如图2所示。该物理模型将分布器、管箱筒体及气液进出口作为一个整体考虑,其难点之一在于如何划分入口分布器的结构化网格。

图2 入口分布器几何结构及网格示意图
由图2(a)可知,该分布器结构较为复杂,采用非结构化形式易生成四面体网格,但其大部分网格界面与流体流向不垂直,因而会影响计算精度。基于上述考虑,本次模拟采用结构化网格对分布器进行分割,使各部分结构相对规整,进而分区域划分六面体网格[1]。同时,在多孔筛板和中心管开孔区域适当加密网格,最终得到的网格数约为4.7×105,如图2(b)所示。通过调整网格疏密对模拟结果进行比较,发现在此基础上继续增加网格数量,模拟结果变化不大。
1.2 多孔介质模型
由于多孔筛板存在上万个孔,对其进行真实建模计算不可行,因而采用多孔介质模型[2]对其进行求解。在多孔介质模型整体尺寸的计算中,多孔筛板的压降问题是关键。由经验公式(1)可见,在流体密度、流量及孔板厚度一定的情况下,多孔介质阻力系数与压降成正比。

式中:C2表示多孔介质阻力系数;ρ表示气体密度,kg/m3;v表示孔板名义流速,m/s;qV表示气体体积流量,m3/s;A 表示孔板面积,m2;δ表示孔板厚度,m;p表示孔板压降,Pa。
为获取多孔筛板的压降数据,采用缩小尺寸的测压模型进行计算,即维持边界条件和物性参数基本不变,改变入口流量,以线性尺寸的平方关系缩小一定比例,尽可能地还原真实情况,如图3所示。针对测压模型在流场、速度场(包括过孔速度等)及压力场的分布等方面的模拟,可以较好地体现真实结构的情况。当然,误差是不可避免的,例如孔板靠近壁面的部分会存在一定程度的失真。

图3 多孔筛板缩小尺寸测压模型示意图
由公式(2)可得,孔隙率ε=0.04。维持孔隙率ε和小孔直径d不变,令孔数n=97,计算得到测压模型直径D=200 mm;令L=4D=800 mm,则可确定测压模型的几何结构,对其进行建模,划分网格并局部加密,如图4所示。
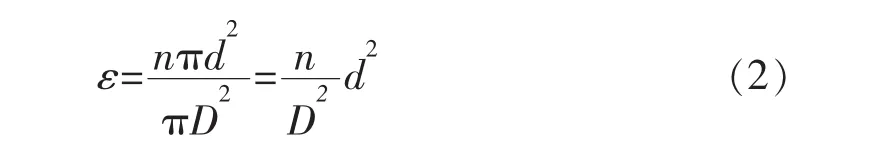

图4 测压模型几何结构及网格示意图
在计算多孔介质阻力系数时,选用表观速度作为多孔区域内的流体流速;在复杂结构中,流体流经多孔区域的真实速度会因条件不同而改变,因而较少采用。
1.3 计算条件及模型设定
对于不可压缩的牛顿流体,在宏观热能守恒的假设下,分布器内流体流动必须满足三大方程,即连续性方程、纳维-斯托克斯(Navier-Stokes)方程、能量方程。
(1)测压模型设定
测压模型内介质为气体,其稳定工作时,可看作定常流动。定义入口为速度入口边界,可根据公式v=qm/ρA计算求得;定义出口为压力出口边界,给定静压,并允许适当的回流。采用k-ε模型考虑湍流效应对流动的影响,并采用高阶精度离散格式进行求解,以保证计算结果的准确性。
(2)入口分布器设定
分布器内介质为气液两相流,在稳定工作时,可看作定常流动。定义两相入口均为流量入口边界,可根据实际工况确定流体流量;定义分配器出口为压力出口边界,给定静压,并允许适当的回流。入口混合分布器、封头、管箱内壁等定义为不可渗透、无滑移绝热边界条件。由于气液混合流动,故采用均相模型去等效,并采用k-ε湍流模型进行求解。
2 计算结果与分析
2.1 测压模型压力分布特征
图5为测压模型对称截面上的压力分布云图。由图5可知,气相进出口压降约为5.2 kPa,其阻力降主要在孔板区域产生。由经验公式(1)可得多孔介质阻力系数C2=4.65×105,该值为后续分布器多孔筛板采用多孔介质模型提供了理论基础。

图5 测压模型对称截面压力分布云图
2.2 浮力模型对分布器内流场的影响
图6为入口分布器在有无设置浮力模型下模拟得到的液相流线分布情况。浮力是密度扰动量的函数,密度扰动量为实际密度与参考密度的差值[3]。图6(a)为未设置浮力模型时,可知,液相流线较为规整,液体由中心管开孔区域流出后,在气体的夹带下,呈葫芦状离开分布器向管板聚集,其流动靠近中心区域;在设置浮力模型后,由图6(b)可以看到,液体流动占据分布器大部分混合区域,靠近中心处速度流线较紊乱,出现了漩涡流。

图6 有无浮力模型的入口分布器液相流线分布对比
图7显示了入口分布器在有无设置浮力模型下模拟得到的出口截面液相体积分数分布。图7(a)中的液相体积分数由中心沿径向逐级递减,至一定距离后,不存在液体分布;而图7(b)中的液体主要分布在截面靠近外侧区域,靠近中心部分分布较少。

图7 有无浮力模型的出口截面液相体积分布
显而易见,由中心管喷出的液体,由于密度远大于气体,会出现下沉的趋势,而经过多孔筛板的气体则向上托起液体。与此同时,靠近中心管区域(内侧)液体较多,不易夹带,而远离中心管区域(外侧)液体较少。因此,少量液体由外侧被气体向上携带,内侧液体逐渐向外侧流动,被携带的部分液体由于中心区域气体较少而向下回落,形成回流旋涡。由此可见,由密度差异引起的自然对流对分布器内气液两相混合的影响很大,不可忽略。
2.3 入口分布器气液分布特征
为考虑两相混合过程中密度差异引起的自然对流问题,模拟应启用浮力模型,并给定相应的参考密度,以避免计算过程中的舍入误差。
图8显示了入口分布器内的气液两相流线分布。由图8可知:气体在进入分布器后,流线出现扩散、回流等现象,流动极为复杂;但经过多孔筛板后,其流动方向基本一致,且分布较为均匀。可见,多孔筛板对于气相均布起到重要的促进作用。
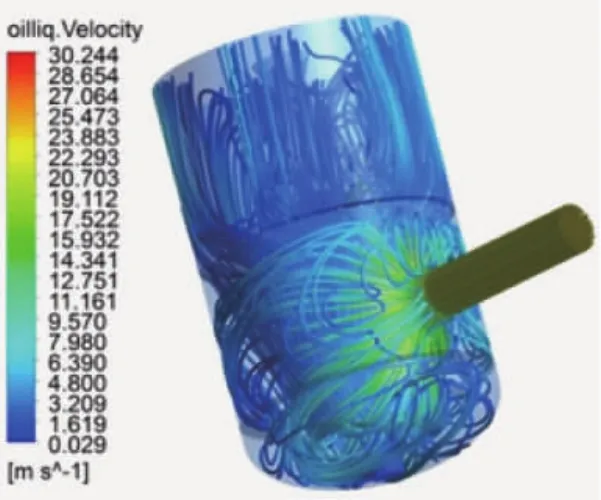
图8 入口分布器内气液两相流线分布图
图9显示了分布器内气液两相的速度和流线分布。由图9可知,在入孔板前气相速度分布不均匀,过孔板后速度分布趋于均匀,但由于气液两相的自然对流,中心管附近气相流动呈无规则旋流状,外侧气相流速较大,易夹带液体。

图9 入口分布器气液两相速度分布图
图10显示了出口截面气液两相体积分数分布。由图10可知,液体主要靠近外侧区域分布,中心管区域分布较少,气液混合有待进一步优化。
3 结论
通过对高效单旋式换热器入口分布器进行数值模拟与分析,得到如下结论:
(1)在气液两相流动中,为考虑由密度差异引起的自然对流问题,模拟过程应启用浮力模型,并设置相关参考密度,以避免计算舍入误差。
(2)在入孔板前气相速度分布不均匀,过孔板后速度分布趋于均匀,可见多孔筛板对于气相均布起到重要的促进作用。由于自然对流的影响,液体主要靠近外侧区域分布,中心管区域分布较少,气液混合有待进一步优化。
采用CFD技术对入口分布器进行模拟分析,较好地弥补了产品结构试验困难的不足,同时也为相关结构优化提供了理论基础和解决方案。

图10 出口截面气液两相体积百分率分布图

