Mathematical Modeling and Solution of 2K-H Planetary Gear Transmission Optimization Design
Shi Suhua
(Shandong Ethnic Secondary Professional School,Weifang,Shandong 262500)
Abstract:By studying the design requirements of 2K-H planetary gear train and analyzing various constraints,the mathematical model is established with the goal of minimum volume.After determining the design variables and establishing the objective function,the constrained variable scale optimization algorithm and Fortran programminglanguagewereused tosolvetheoptimization problem.
Keywords:planetary gear transmission;optimization design;m-mathematical modeling
Compared with ordinary fixed shaft gear drive,involute planetary gear drive has the advantages of large carrying capacity,small size,high efficiency,light weight,large transmission ratio,low noise,high reliability,long life,easy maintenance and so on.It is widely used in the transmission systems of cars,heavy-duty trucks,engineering vehicles and aircraft[1].
It is pointed out that,with the same manufacturing accuracy,compared with the fixedaxis drive,the load of planetary drive is generally better distributed along the tooth width[2].This is because the ratio of tooth width to diameter in a planetary transmission is generally less than 0.7,whereas it is 1.6 in a conventional reducer and,in rare cases,such as in a turbine reducer,is significantly greater than this.Under the same conditions,the weight of the planetary transmission box is several times smaller than that of the ordinary fixed shaft gear transmission box,because the outer dimensions of the planetary transmission box is much smaller than the ordinary fixed shaft gear transmission box.
When designing planetary transmission,it is more important to select gear parameters correctly than to design ordinary fixed shaft transmission.Improper selection of gear parameters may not only lose the advantages of size and weight,but may even get atransmission that isnot conducivetouse.
It is very effective to optimize the design of planetary gear mechanism according to the objective of minimum volume,not only to reduce the volume,but also to reduce the quality,save materials and reduce costs,etc.,which are especially important for productssuch as automobiles and aircraft[3].The 2KH planetary gear mechanism commonly used in such productsisnowused for optimization design.
I. 2K- H Planetary Gear Design Requirements
For the 2k-h planetary gear,as shown in the right figure,in order to design a planetary gear transmission that meets the requirements,several parameters of the gear should be determined according to the known conditions:the number of teeth of each gear z,modulus m,and tooth width b.if the number of planetary gear is also taken as the design variable,then there are four parameters.According to the knowledge of mechanical design,the parameters of planetary gear should meet the following two conditions:one is the geometric design condition,which is the condition of the gear"s normal transmission without considering the material"s view of the gear as a rigid body;The second is the strength condition of the gear.As a mechanical component,planetary gear requires certain strength requirements under the condition of determining materials to ensure that the gear reaches the expected life[4].The followingisadetailed analysis.

(i)Geometric Design Conditions of Planetary etary Gear Transmission ssion
According to the mechanical design knowledge,in the planetary gear train,the gear number selection should meet the following four conditions.
1.Transmission ratio conditions.Ensure that a given transmission ratio isachieved.
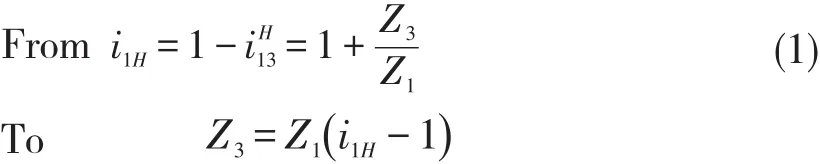
2.Ensure that the axes of the two center wheels and the tie rod coincide,that is,to meet the coaxial condition(concentric condition).
When standard drive and equidistant displacement drive are used,we can get

3.Ensure that each planetary wheel can be evenly loaded between the two center wheels,that is,tomeet theassembly conditions(correct gear).
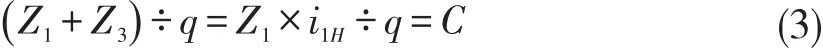
q-number of planetsround,C-positiveinteger
4.Ensure that the planetary wheels do not collide with each other,that is,to meet the adjacency conditions.
To ensure that the top teeth of the two adjacent planetary wheels do not touch each other,the center distance of the two adjacent planetary wheels should be greater than the diameter of the top tooth circle of theplanetary wheel.
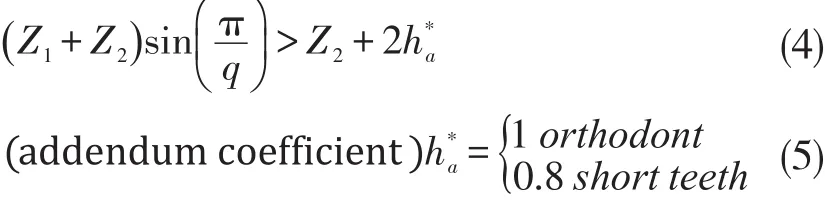
(ii)Planetary Gear Transmission Strength ength Design esign
1.Contact Fatigue Condition of Tooth Surface
Thecheck formulais
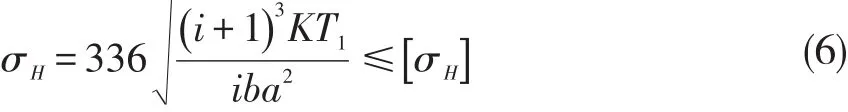
In theformula
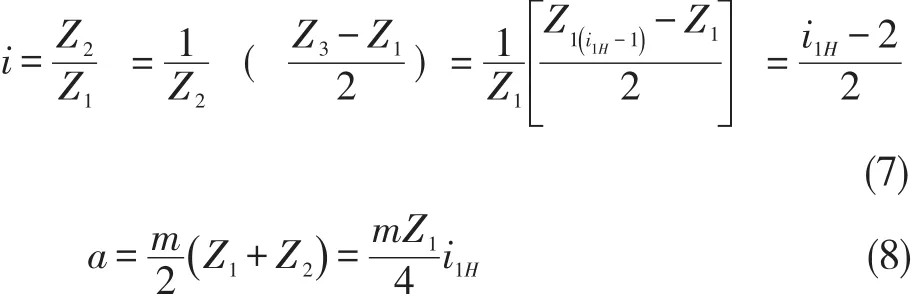
K-loading coefficient
T1-torqueof gear 1
P-transmitted power
n1-speed of gear 1
b-calculatethetooth width
m-moduleof gear
[σH]--allowable contact stress(MPa)
Thesortingresult is

2.Fatigue Condition of Tooth Root Bending
Thecheck formulais

YF-tooth formfactor
[σF]-allowablebendingstress(MPa)
Theresult of simplify is

(iii)Other Design Conditions tions
1.Un-undercut Condition

2.Limit of Tooth Width

II.Establish Optimization Mathematical Model
(i)Determine Design Variables ables
Take the number of teeth(Z1),modulus(m),tooth width(b)and number of planetary wheels(q)of thecentral wheel asdesign variables,that is

(ii)Determine the Optimization Objective ctive Function ction
The optimal design is carried out according to the minimum dead weight,and the sum of the volume of the central wheel 1 and the planetary wheel is taken as the weight index of the planetary gear transmission.The objective function can be expressed as follows:
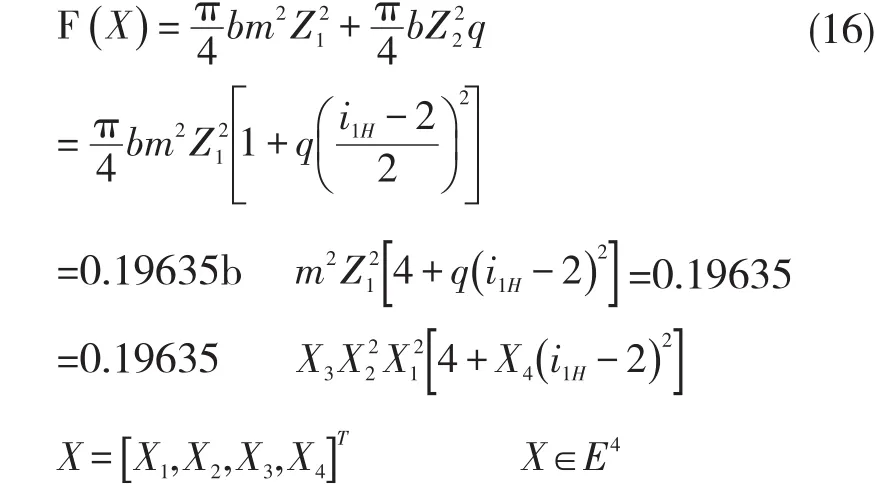
(iii)Determine Constraints aints
1.Geometric Constraint
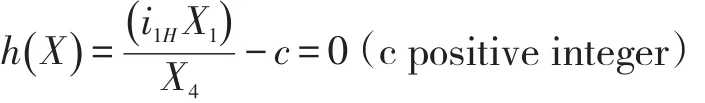
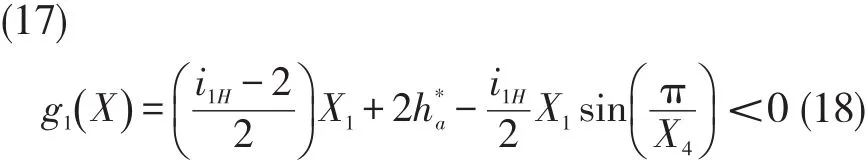
2.Strength Constraint

(iv)Other Constraints aints
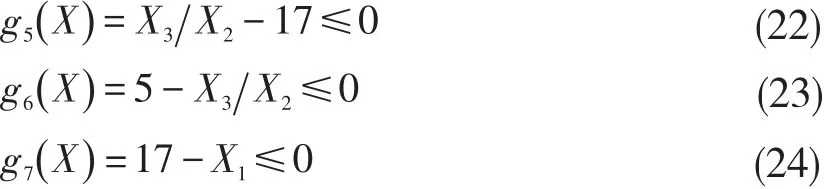
(v)Establish Optimization Mathematical Model Model

Xl,Xuare the upper and lower bound vectors of the design variable X→respectively.
III.Optimization Solution of Planetary Gear Mechanism
From the above analysis,it can be seen that the optimization solution of planetary gear mechanism is to solve a four-dimensional constraint problem,taking into account some variables for shaping.Therefore,in summary,the optimization process of 2k-h planetary gear mechanism is divided into two stages:The first step is to treat the design variable as a continuous variable to solve the minimum value of the objective function;The second step is to round and standardize each real type component(parameter)of the obtained minimum value.The optimal design parametersare obtained fromabove.
For the solution of mathematical model,the constrained variable scale method is adopted,Fortran language was used for programming solution.
IV.Design Example
A planetary gear drive,the transmission power P=4.78MW,the transmission ratio i1H=3.45,the output speed nH=487r min,and the material strength of the gear is[σH]=960MPa,[σF2] =378MPa,[σF1]=310MPa,respectively.
According to the known conditions,put into the established mathematical model,for the value of YF,scatter the curve into 24 points and use interpolation algorithm to value.
In addition,limit the upper and lower limits of design variables:

After the above solution,the following results can beobtained:
Z1=73,Z2=53,Z3=179,B=56mm,m=3.75mm,q=7
V.Conclusion
The above mathematical modeling process and design examples,it can be seen that the establishment of the mathematical model planetary gear transmission optimization problem has been solved,the results calculated in the design example and theactual dataareconsistent.

