联合有社交意识的D2D配对和功率分配策略

王海波,全文奇

(北京交通大学 宽带无线移动通信研究所，北京100044)

D2D通信可以利用移动设备的近距离特性，使设备之间能够直接通信.通过D2D通信，可有效地从蜂窝网络中卸载数据流量，并且D2D对也可以复用蜂窝链路资源.这两个因素可以提高系统的吞吐量和频谱效率，为了获取这些潜在的增益并减少D2D对之间的干扰，需要仔细设计匹配机制和无线资源管理的算法[1].文献[2]通过利用用户之间的位置信息提出了一种集中式的D2D发现机制.该方案能够自适应地给D2D对分配信道资源，避免了在LTE-A系统中基于随机接入过程频谱资源利用不足的问题.文献[3]提出了一种基于编码的D2D发现协议，该协议利用包含移动应用压缩信息的码字，来查找对这些移动应用程序感兴趣的邻近设备.文献[4]引入斯塔克尔伯格博弈来求解D2D通信中的干扰协调问题.

近年来，将社交网络与D2D通信结合的技术研究也已经引起了广泛的关注和研究.社交信息可以反映用户之间的密切程度.用户之间有密切的社交关系在某种程度上可以共享彼此感兴趣的内容[5].文献[6]引入社交关系到D2D通信中来解决资源分配问题，并且研究了社交群体效用最大化的博弈问题.文献[7]则利用社交网络的特性来解决资源分配和干扰管理的问题，并提出了一种有社交意识的D2D通信系统.

尽管结合社交网络的D2D技术的相关研究工作已经有很多研究成果，但是仍然存在诸多挑战需要解决.首先，用户的真实社交信息应该被考虑在网络模型中来确保系统的准确性和可行性.然而现有的大部分工作都是假定用户的社交信息遵循一些理想的统计模型，忽略了实际社交信息的不确定性和复杂性.其次，由于D2D对复用频谱资源，复用相同信道导致的干扰问题应该通过有效的功率分配策略来协调.综合考虑上述的两个方面，本文作者将引入用户之间的真实社交信息并且提出一种联合D2D配对和功率分配的策略.

1 联合社交的D2D通信系统模型

本文的系统模型如图1所示.在该模型中，考虑一个单小区的情形，即只有一个基站，在基站的周围随机分布着一定数量潜在的D2D用户对(Device to Device Users Equipment，DUEs).这个场景中，假设DUEs能够自主地进行设备发现和内容共享.本文提出的网络模型包含两个域：物理域和社交域.

1)物理域：在物理域中，假设D2D处在overlay的模式，这种模式下，D2D被分配独立的频谱资源并且所有的D2D对共享该频谱资源.因此，在DUEs和传统的蜂窝用户(Cellular User Equipment，CUE)链路之间不存在干扰，只有DUE之间的相互干扰.如图1所示，这里有三对D2D对在一个小区中，它们共享同一信道并且相互干扰.

2)社交域：在物理域中的每个用户都对应于社交域当中的一个人，因为设备终端是由人持有的.在平时的日常生活中，人们通常在各种话题中，选择与自己有相同兴趣的人相互交流.例如，假设图1的场景是一个办公区域，其中的Bob愿意和同事分享文件和商业观点；Lily则喜欢在自己的休息时间和同事分享一些自己喜欢和感兴趣的内容，如图片、视频、新闻和体育赛事等.

图1 系统模型示意图Fig.1 Illustration for system model

无线信道衰落模型考虑所有D2D链路间的大尺度衰落并且有独立同分布的瑞利小尺度衰落.信道的噪声为加性的高斯白噪声.

对一条D2D链路分析，假设第u个D2D发送者的发射功率为pu，对应于第v个D2D接收者的接收功率为pv，因此有

(1)

式中：du,v为D2D发送者到接收者的通信距离；α为路径损耗的衰落因子；ku,v为两者之间的瑞利衰落因子.

因此，得出在D2D接收端的信干噪比(Signal to Interference plus Noise Ratio，SINR)为

(2)

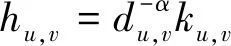
(3)

设每个D2D的通信带宽为w，根据香农公式，得到单个D2D通信的链路速率为

Ru,v=wlb(1+γu,v)

(4)

将式(3)带入式(4)可得链路速率为

(5)

2 问题规划

在本节中，将系统模型进行数学建模.首先，引入物理图和社交图来建模系统中的物理域和社交域.接下来，基于上述提出的图的模型来进一步进行问题的规划.

用u∈{1,2,…,U}来表示D2D中那些主动发送配对请求的用户，相应地，用v∈{1,2,…,V}来表示那些被动接收来自其他D2D请求信号的用户.因此，定义如下的相关图：

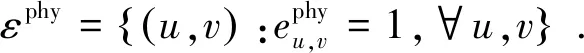
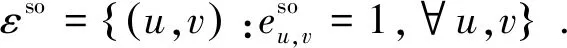
基于以上提出的图的模型，定义整个系统带有权值的吞吐量为

(6)

式中：β代表最终匹配后的结果集合；p是最终的所有用户的功率集合；βu,v是用户u和v的匹配结果；w是信道带宽.给出使整个系统吞吐量最大化的目标函数的形式为

(7)

式中：C1～C3是匹配的约束条件.C1中，只有当βu,v=1时用户u和v配对，βu,v=0时不进行配对.C2和C3表示每个用户只能且最多和一个用户进行配对，这就限制了该匹配过程是一个一对一的匹配类型.C4是功率分配的约束条件，其中P是最大的用户发射功率.

式(7)中的最优化问题是一个MINLP，因为其中既包含了非线性的目标函数，同时也耦合了整数和连续变量，且已经被证明是个NP-hard[10]问题.因此，为了有效求解该问题，将整个问题解耦拆分为：1)假设所有用户的分配功率已知并且固定不变，求解D2D配对的问题.2)假设D2D的配对已知，解决功率分配的问题.

3 问题求解

3.1 给定功率分配时的D2D配对算法

假设功率分配已知，即每个用户的发射功率p已知，式(7)则可以被简化为一个整数规划的问题

(8)

对于式(8)，按照最优化理论，该类型的数学问题经典的解法包括动态规划和分支定界法，这两种方法的本质上还是一种搜索算法，并且虽然这两种方法搜索空间可以递归减少，但是随着用户数量的增多，算法的复杂度也会急剧增加.因此，在实际的大规模无线网络中，建立在匹配理论上算法复杂度较低且更加实用[11].

基于匹配博弈理论以及相应的匹配类型，结合式(8)的约束条件C2和C3，该问题可以定义为一个一对一的双边匹配问题.在这个博弈中，用户u和v互相选择自己最喜欢的用户.这种用户的决策是以双方相互建立的偏好列表为基础的，具体的偏好列表和设定情况如下：

1)用户u的偏好.在配对之前，对于用户u，需要找到邻近的D2D用户.主要过程是处在系统中的用户u收集用户v的社交信息和物理信息，具体实施过程设定如下：①用户u发送信标来找到其他的D2D接收者，并从基站获取其各自的物理信息.因为本文的重点是在配对的过程，因此暂不考虑D2D用户发现过程的信令开销和能耗.②用户u从MSN应用程序获取与它已经发现了的D2D用户的社交信息.在获得物理和社交信息之后，用户u基于下面的条件来决定向哪些用户来发送配对请求

(9)

式(9)意味着从D2D发送者的一方来看，发送配对请求的目标用户需要在物理和社交上同时满足距离在最大的D2D通信范围之内和社交强度不小于设定的社交门限的条件约束，满足这样条件的用户v才能成为后选者.最后，用户u给满足条件的所有候选者发送配对请求.

2)用户v的偏好.在收到所有的D2D的配对请求信号后，用户v来选择到底愿意和哪个u做配对.这里用户v的偏好设定为收到的SINR.更高的SINR将会增加优先选择和优先配对的概率.

基于以上的分析，结合匹配理论的知识，本文设计了一种基于匹配理论的D2D配对算法,即算法1.

算法1：D2D用户配对算法

1：初始化：用户u∈{1,2,…,U}寻找邻近用户v∈{1,2,…,V}.然后，用户u测量和收集它邻近用户的物理和社交信息；

2：Foru∈{1,2,…,U}do

4：End For

5：Forv∈{1,2,…,V}do

6： 等待收集所有的D2D配对请求信号R

7： IfR∉Ø then

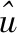
8： End If

9：End For

10：输出：D2D配对结果β

算法的匹配过程主要包含以下3步：

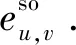
2)用户u发送请求.每个u基于式(9)的偏好条件依次发送D2D配对请求给v基于它们的偏好条件在式(9)中.

3)在收到配对请求后，用户v等待直至收到所有来自u的请求，然后选择自己最愿意接受的请求者，同时拒绝其他的请求者.

3.2 给定D2D配对时的功率分配算法

假设在系统中D2D的配对阶段已经完成，重点关注如何合理地进行功率分配才能使整个系统的吞吐量最大化的问题.同样地，对式(7)进行在功率变量上的问题解耦，即假设D2D的配对结果参数β已知，式(7)可以变为

(10)

假设有m个用户已经配好对,则p={p1,p2,…,pm}代表每个用户的发射功率集合.为了解决式(10)非凸目标函数的最优化问题，本文采用了D.C.规划，主要的思路是通过将对数形式的一个目标函数转变为两个对数相减的形式，再多次迭代，得到一个近似最优解[12].

首先，将式(10)变成一个两式相减的形式，即

Rtot(p)=f(p)-g(p)

(11)

其中：

(12)

式中:f(p)和g(p)是关于p的凸函数.为了找出一个和变换后问题等价的最优解，推导出g对于p的梯度形式如下

(13)

在式(3)～式(13)中，au为一个U维实数空间的向量，au∈RU，有

(14)

通过利用梯度形式，产生了一个改进的可行解的pk(k=1，2,…，N)序列，pk是第k次迭代产生的对应下面目标函数式的最优解

(15)

本文设计算法2求解式(10)的功率分配问题.其中，最优的功率分配方案可以通过迭代求解式(15)获得[13].

算法2：D2D用户功率分配算法

1：初始化：设置初始的功率分配方案p0，迭代次数初始值为1，迭代终止门限ε；

2：重复：

3：k=k+1

求解式(15)得到最优的解p*；

设置pk=p*

4：直到：|Rtot(pk)-Rtot(pk-1)|≤ε；

5：输出：D2D功率分配结果p；

通过上述分析，可以得出以下信息.

因为g(p)是凹的，因此有

g(p)≤g(pk)+(g(pk),p-pk)

(16)

因为对于式(15)总是一个可行解，结合式(16)，可以推出

f(pk+1)-g(pk+1)≥f(pk)-(g(pk)+

(17)

即，求解得到的pk+1总是比pk更优.并且因为本文设计的约束条件是一个紧的约束，根据柯西定理，pk总是收敛的，所以在经过有限次的迭代最终能求出最优的解.

3.3 结合社交的D2D配对和功率控制算法

前面的工作主要通过问题的解耦，对解耦后的两个子问题进行问题的研究和解决，即式(10)和式(8)，然而最终的问题规划是式(7)，因此,本文提出了一种结合社交的D2D配对和功率分配策略(Joint Social-aware D2D Pairing and Power Allocation，JSDPPA)，即算法3.

算法3：JSDPPA

1：初始化：

1)用户u∈{1,2,…,U}寻找邻近用户v∈{1,2,…,V}.然后，用户u测量和收集邻近用户的物理和社交信息；

2)设置最大的迭代次数N和最大的门限θ，迭代初始值n；

3)设置初始的配对策略和功率分配策略{β(1),p(1)}；

2：Forn=1,…,Ndo

3： 对于给定的p(n)，计算D2D配对β(n+1)通过算法1；

在得到β(n+1)后，计算功率分配p(n+1)通过算法2；

5： 设置最优的D2D配对和功率分配为{β*,p*}={β(n),p(n)}

6： Else

7：n=n+1；

8： End If

9：End For

10：输出：D2D配对结果和功率分配{β*,p*}；

算法3主要包含3个步骤：1)在初始化阶段，给定功率分配，按照之前提出的算法1解决D2D的配对问题；2)在得到D2D的配对结果后，根据前面的算法2解决功率分配问题；3)重新将2)中得到的功率分配的结果代入到1)来再次求解D2D的配对问题，整个过程重复迭代，直到结果最终收敛.

算法3的时间复杂度为Ο(N×|u|×|v|+N×Nd.c)，其中|u|×|v|是算法1收敛的迭代次数，N和Nd.c是算法2和算法3需要收敛的迭代次数.

4 性能评估

相比已有的研究工作的,本文创新之处在于考虑用户的真实社交信息，并将其设定为影响D2D配对和功率分配的重要因素.为了使整个用户的社交关系更加可视化，基于Facebook数据集[14].利用数据分析工具gephi[15]来生成可视化的社交网络图,见图2.本文所采用的用户社交数据记录着用户在一个月的相互之间的接触频率，因此可以映射生成了一个带有边权重的社交图.

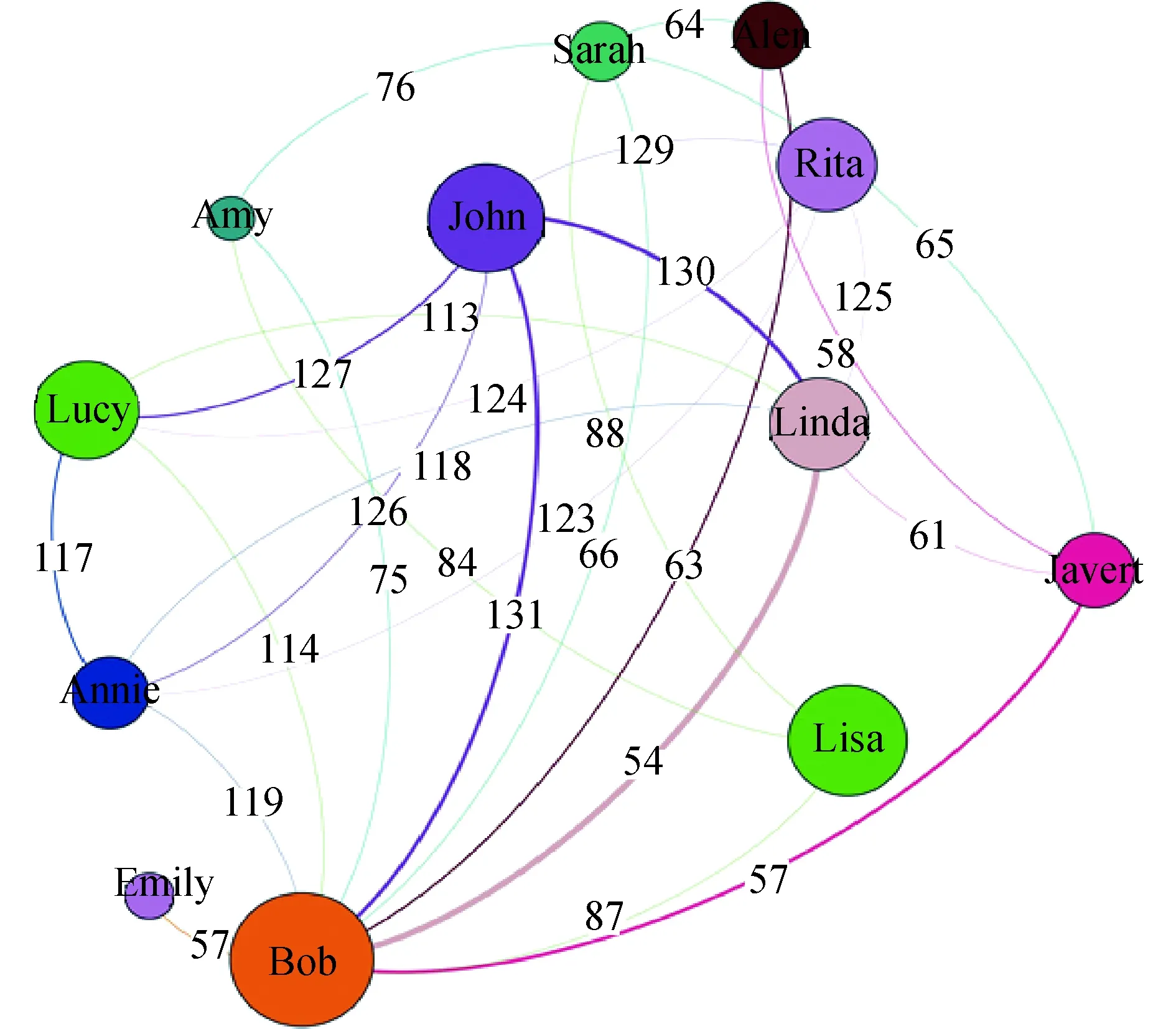
图2 基于真实社交网络生成的社交图Fig.2 Generated social graph based on real-life social network

图2中将一段时间内用户间交互频率的门限设置为tth=50.其中的节点代表在社交网络中的用户，每条边代表不同用户间的社交关系，每条边上的数字代表不同用户间的接触频率，而且只有两个节点间的接触频率大于门限值才让其之间有边存在.

在Matlab仿真中，考虑一个单小区的D2D网络，主要的仿真参数见表1.

表1 仿真参数

4.1 功率分配策略的性能

在算法2中，利用多次迭代的方式来找到最优的功率分配策略，仿真结果如图3所示.

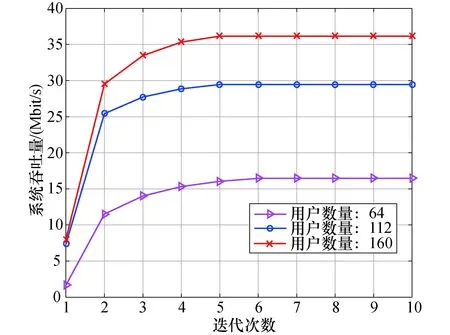
图3 算法2的收敛性Fig.3 Convergence of alogrithm 2

图3反映了不同用户数量情况下系统吞吐量和迭代次数的关系，很明显，可以看到在经过6次迭代后系统的吞吐量基本总是收敛，相应地用户数量从64,112到160.其他几个数量的用户情况类似，所以只挑选上面3种数字情况来代表说明.随着整个用户数量的增加，系统的吞吐量也是逐渐增加，且增幅逐渐减小，主要是因为随着D2D数量增加，更多的用户共享同一频谱资源，就会产生更多的同信道的干扰问题，导致链路的速率下降，从而使整个的系统吞吐量增加缓慢.基于以上的整体分析，说明了算法2是可以保证收敛的.

4.2 JSDPPA算法的性能

图4反映了本文提出JSDPPA的算法性能，并且与其他两种策略进行比较，策略1的算法是考虑联合D2D配对和功率分配的算法但是没有考虑用户的社交性能；策略2的算法是有社交意识的D2D配对但是并没有进行功率分配[6].

从图4中可以观察出3种策略的整体趋势都是随着用户数量的增加，系统的吞吐量显示随之逐渐增加，然后随着网络中的DUE数量趋于饱和，3种策略都各自在某个拐点之后开始下降，这个原因是因为随着用户的数量增加，产生更多的干扰影响了整体的性能.此外还可以发现，与策略1和策略2相比较，JSPPA得到了一个合理的增益.策略1的性能最差，因为它并没有考虑D2D用户间的社交关系，使得配对过程可能出现用户之间相互竞争，导致系统干扰增加，性能下降.当D2D的用户总数不超过96时，JSDPPA和策略2在系统吞吐量上差别不大，但是当用户数超过96时,JSDPPA明显要优于策略2.

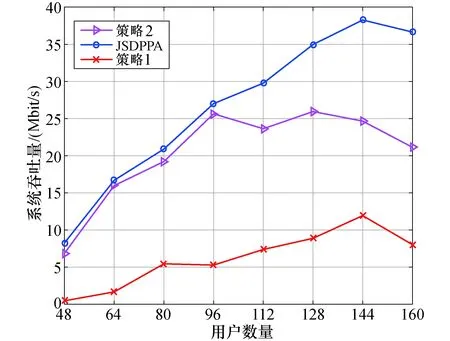
图4 不同用户数量的系统吞吐量Fig.4 System throughput verus total D2D user numbers

此外，当D2D用户的数量不超过96时，JSDPPA和策略2都是快速增长，这是因为当D2D用户的数量增多时，与用户u有较强社交关系的用户v的数量增加，从而促使匹配成功的概率增加.然而，当D2D数量更大时，用户之间的干扰也变得更加严重，策略2的吞吐量明显开始降低，而JSDPPA则可以有效缓解复用相同信道的带来的干扰并获得更高的增益.

5 结论

1)研究了D2D通信中联合有社交意识的D2D配对和功率分配的问题.具体来说，本文提出一个三步法的算法来解决该问题.第一步：假设功率分配已知，求解了D2D配对的问题，在该步骤中，以一对一的双边匹配博弈为理论基础，结合经典的匹配理论中的算法设计了算法1；第二步:假设D2D配对已知，求解功率分配的问题.为了使问题可以求解，通过变形和参考D.C.规划，最终将问题变成了一个等价的凸问题，并设计出了迭代求解的算法2；第三步:基于前两步的研究基础，设计了一种迭代实现的算法3，称之为JSDPPA，通过该算法获得最终的最优解.

2)利用真实的社交网络的公开数据集并提取部分数据对D2D系统的吞吐量进行了仿真，并且与其他两种策略进行了性能比较，仿真结果表明本文提出的JSDPPA策略在很大程度上优于其他两种策略，证明了本文方法的有效性.