新型高温超导磁浮车辆通过曲线时的运动学规律
邓 斌 陈 武 邓自刚 霍文彪 尹智慧
(1.西南交通大学机械工程学院,610031,成都; 2.西南交通大学牵引动力国家重点实验室,610031,成都; 3.中车唐山机车车辆有限公司, 063035,唐山//第一作者,教授)
高温超导磁浮列车作为一种新的轨道交通运输工具,主要依靠高温超导体与永磁轨道之间的作用力将列车悬浮于空中并进行自导向,从而实现列车与地面轨道间的无机械接触,再利用感应板与定子线圈之间的相互作用驱动列车运行[1]。这与传统的轮轨式列车依靠车轮与轨道之间的刚性接触约束实现支撑和导向有本质的区别。在曲线轨道上,传统转向架运动状态主要是轮轨相互作用的结果,而高温超导磁浮转向架的运动状态主要依靠超导体自导力实现,其在曲线上的运动状态是自导力、离心力、悬挂力等诸力平衡的结果。因此,不能运用传统轮轨车辆曲线通过理论分析磁浮车曲线通过时的运动学规律和计算各相关尺寸的几何关系[2]。文献[3]研究了磁浮列车过曲线时仅受自导力作用达到平衡状态的情况,未考虑离心力的作用。但实际上在曲线上运行的列车所受到的离心力对其平衡状态影响也很大。为此,本文从超导体自导力和离心力共同作用达到平衡入手,探究高温超导磁浮列车通过曲线时转向架和车厢的位置状态及其与磁轨之间的相互几何关系[4],为高温超导磁浮转向架曲线通过的设计计算及运动学分析提供一定的理论依据。
1 模型结构和平衡关系
1.1 模型几何结构
本文主要参考现有动车组转向架结构[7],在该基础上,针对磁浮车辆的运行要求设计出新型高温超导磁浮转向架。该转向架既不同于传统轮轴式转向架,也不同于目前常导低速磁浮车辆采用的集成电磁铁和直线电机的独立模块式转向架,而是一种通过关节轴承铰接成一体的横梁组式转向架。该转向架以杜瓦梁为悬浮基本结构部件,以轨道感应板作为驱动载体,集成机械导向接口,能够实现悬浮、导向和驱动功能。
新型高温超导磁浮车辆包含2个转向架。每个转向架主要由2个横梁与1个上构架构成,其结构模型如图1所示。转向架结构均采用6061-T4铝合金材质,实现了整体结构明显的轻量化。为了使转向架适应磁轨线路要求,横梁与上构架之间创新性地使用关节轴承组作为主支撑,成功实现了横梁与上构架之间的全解耦,横梁可以在x、y、z三个方向转动,使转向架过曲线时在自导力作用下灵活转弯。关节轴承组结构模型如图2所示。在横梁两侧分别设置有弹性滚子旁承辅助支撑。牵引拉杆装置安装于上构架。杜瓦通过螺母连接在杜瓦梁上,使杜瓦中线与杜瓦梁中心线重合,杜瓦梁为横梁的一部分。感应板与横梁之间通过螺栓连接。车厢与转向架之间主要参照动车转向架二系悬挂装置的连接方式。

图1 转向架结构模型图
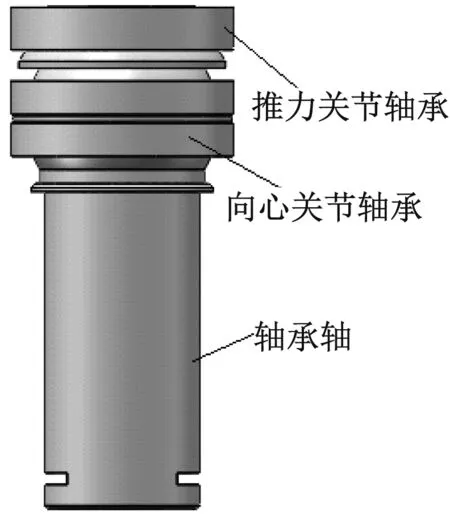
图2 关节轴承组结构模型图
1.2 平衡关系
高温超导磁浮车辆过半径为R的曲线时,转向架在曲线上的位置状态是由超导体自导向力、离心力等各种力综合作用的结果。车厢与转向架及其磁轨之间位置运动关系复杂,需要通过分析几何结构关系,在平衡状态时推导出相应的结论。为了确保转向架能顺利通过曲线轨道,磁浮列车的超导体不仅提供了垂直方向的悬浮力,而且提供了横向的自导向力保证转向架的横向定位[11]。在作曲线通过分析时,转向架的位置状态主要是作用在转向架上各种力平衡的结果,因此本文主要考虑超导体自导向力与离心力相互作用对车辆过曲线能力的影响,而忽略其他力的作用。
转向架在曲线磁轨上达到平衡主要依靠杜瓦梁与磁轨直接相互作用,因此首先分析杜瓦梁与磁轨的相互关系。在过半径为R的曲线时,杜瓦梁不能弯曲,杜瓦梁中心线与磁轨的中心线会出现一定的偏离,这导致杜瓦梁纵向各点距磁轨中心线横向的距离不同,因此杜瓦梁各处所受到的横向自导力也不同。过半径为R的曲线时杜瓦梁平衡关系图如图3所示。由于超导体自导力的大小与超导体中心线相对磁轨中心线的横向偏移量成线性关系,故超导体单位长度内自导力的大小在图3中通过箭头线表示出来。
若不考虑其他力的作用,则只有当杜瓦梁所受向内的力与向外的力合力数值相等时,杜瓦梁才可在磁轨上达到平衡。如图3所示,各箭头所示部分的合力大小与箭头所表示的面积成正比,因此,可近似认为,磁轨中心线两侧箭头所表示自导力合力的面积与车体所受离心力作用于杜瓦梁上的力所示箭头面积相等为杜瓦梁平衡条件。即杜瓦梁在曲线上处于S2+S3+S4+S5-S1=S4+S5的状态。其中,S1、S2、S3表示超导体自导向力所示的面积,S4、S5表示转向架所受离心力作用于杜瓦梁的力所示面积。设转向架杜瓦梁长为lm,杜瓦梁内外自导向力相互平衡所需长度为l,曲线半径为R,杜瓦梁相对磁轨中心线内、外侧的偏移量分别为Δ1、Δ2、Δ3、Δ4和Δ5,则当杜瓦梁在磁轨上对称平衡时有:Δ2=Δ3,Δ4=Δ5,S1/2=S2=S3,S4=S5。

图3 过半径为R的曲线时杜瓦梁平衡关系图
假设S1=S2+S3且对称平衡,根据三角形正弦定理及余弦定理得:
(1)
(2)
由三角形勾股定理得:
(3)
根据面积等效关系得:
(4)
由积分定理可得:
(5)
由式(1)~(5)解得:
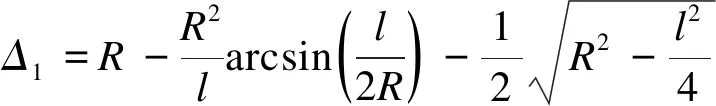
(6)
(7)
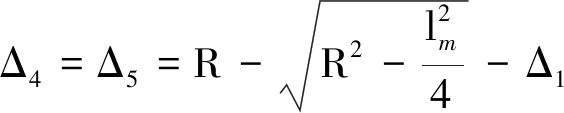
(8)
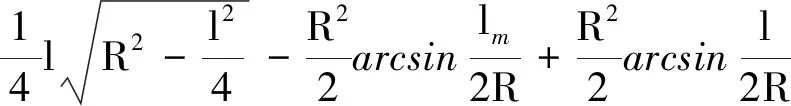
(9)
因为l
(10)
(11)
由式(6)~(11)可得:
(12)
由式(12)可知:当lm/R<0.1时,转向架通过半径为R的曲线达到平衡时,杜瓦梁中心线相对磁轨中心线偏移量Δ1=Δ2=Δ3,杜瓦梁中心线相对磁轨中心线最大偏移量Δ4、Δ5与l相关。
2 磁浮车辆过曲线运动分析
2.1 几何计算
图4给出了新型高温超导磁浮车辆过半径为R的曲线时,在磁轨上达到平衡时的位置关系简图。其中显示了横梁、上构架及车厢中心线之间的位置,横梁与上构架交点为旋转中心,上构架与车厢之间采用空气弹簧连接。在过曲线时,车厢相对上构架之间的转动是以上构架与车厢中心线交点为旋转中心。

图4 车辆过曲线时状态简图
磁浮车辆包含2个转向架,车辆过曲线时,2个转向架在磁轨上的位置状态相同且成对称关系。本文主要分析转向架1及其车厢在半径为R的曲线上的几何位置关系及运动状态。其简图如图5所示。
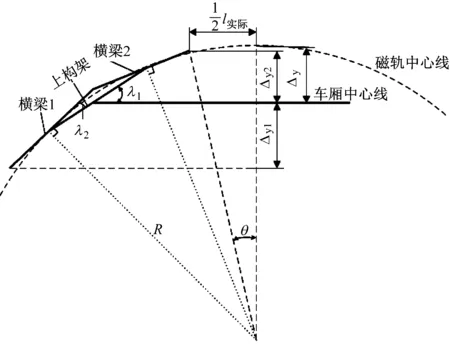
图5 过半径为R的曲线时转向架1及其车厢位置关系简图
设杜瓦梁长度为lm,上构架长度为l上,两转向架之间距离为lm,车厢中心线与上构架之间转角为λ1,横梁与上构架之间转角为λ2,横梁1的杜瓦梁前端相对车厢中心线竖直位移为Δy1,横梁2的杜瓦梁后端相对车厢中心线竖直位移为Δy2,车厢中心线相对磁轨中心线偏移量为Δy,横梁2的杜瓦梁后端与对称线之间的夹角为θ。
为保证两横梁的杜瓦梁在过曲线时不发生碰撞,需在杜瓦梁之间预留一定的安全距离,因此实际杜瓦梁长度为:
式中:
Δl——前后两杜瓦梁之间的安全距离。
根据图5中几何分析可得λ1=3θ,λ2=θ,则:
(13)
(14)
由于杜瓦梁相对磁轨偏移量Δ4与轨道半径相比很小,可以近似忽略不计,则:
(15)
由式(13)~(15)可得:
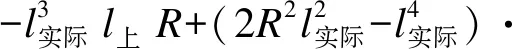
由于压力容器内部满载,压力高达2.16 MPa,在车体尾部保险杠抵消了部分冲击载荷后才遭受碰撞,因此碰撞对压力容器造成的变形较小。压力容器整体的应力如图10所示,压力容器罐体中段上的最大应力单元号为227 074,并对该单元的应力进行绘图,如图11所示。由应力图解可以看出,曲线非常符合实际情况,撞击所带来的冲击载荷在罐体上形成振荡,罐体上的单元应力有形成振荡,随着时间的振荡逐步衰减,趋于稳定。罐体所受最大应力峰值为217 MPa,远没有达到破坏极限345 MPa,可以认为该罐体的强度可以满足实际生产的使用要求。
(16)
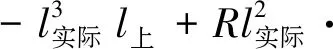
(17)
由图5几何关系可知,车厢中心线相对磁轨中心线偏移量Δy等于杜瓦梁相对磁轨中心线偏移量Δ1与横梁2的杜瓦梁后端相对车厢中心线竖直位移Δy2之和,即:
Δy=Δ1+Δy2
(18)
由式(12)、(17)和(18)可知:

(19)
2.2 设计实例
为探究转向架所用杜瓦在永磁轨道上的横向偏移量与其导向力之间的大小关系,试验中使用了一批相同工艺制备的矩形杜瓦,其尺寸为404 mm×149 mm×94 mm;外磁场采取HALBACH阵列形式[13]的永磁轨道。在FCH 40 mm(场冷高度)情况下进行试验时,高温超导体杜瓦的长边沿着永磁轨道长度方向摆放,且放在与磁轨中心线横向偏移量为10 mm的正上方位置。通过改变杜瓦横向偏移量,测得杜瓦所产生的自导力,绘制杜瓦横向偏移量与自导向力之间的关系图,如图6所示。
在小范围横向偏移量下,杜瓦产生的自导向力与横向偏移量之间为近似线性的关系[14],则由图6可知,杜瓦横向导向力与磁轨中心线相对杜瓦中心线偏移量之间的关系为:
F=102x
(20)
式中:

图6 杜瓦在FCH 40 mm情况下横向偏移量与自导向力关系图
x——磁轨中心线相对杜瓦中心线偏移量,mm。
由式(12)和式(20)可计算出杜瓦梁所受到的自导向力合力为:
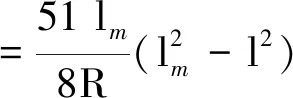
(21)
当所设计转向架的主要尺寸、轨道半径及列车过曲线时未平衡离心力给定时,由式(15)~(17)、式(19)及式(21)可计算出列车通过曲线时的Δy、Δy1、Δy2,以及λ2和λ1。
根据设计要求,新型高温超导磁浮车辆过曲线时未平衡离心加速度a=0.3 m/s2,则车辆所受到离心力F离心力=ma=7 200 N(其中m为新型高温超导磁浮车辆满载总质量,m=24 000 kg)。磁浮车辆上装有2个转向架,其所受到的离心力主要由4个横梁上的8个杜瓦梁提供的自导力来平衡,因此,单个杜瓦梁为平衡离心力所需的自导向力为900 N。 设计的高温超导磁浮转向架主要几何尺寸如下:lm=2 647 mm,Δl=78 mm,l上=2 625.7 mm。则在不同弯道半径下偏移量和偏转角如表1所示。
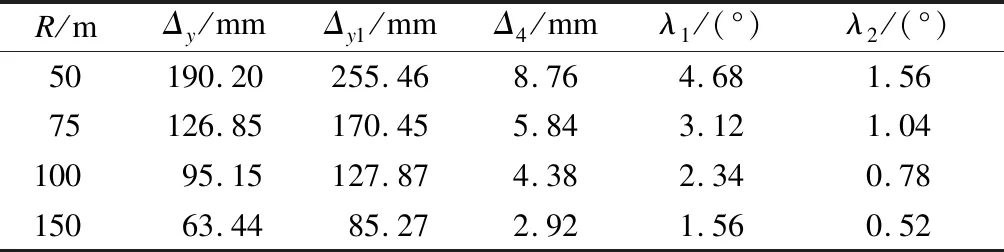
表1 不同曲线半径下的偏移量和偏转角
由表1可知,随着曲线半径的增大,偏移量随之增加,而偏转角随之减小。由于规定的设计磁轨曲线半径为100 m,因而所设计转向架的偏移量和偏转角均满足工程设计要求。
3 结语
本文研究了新型高温超导磁浮车辆通过曲线时,在离心力及自导向力合力作用下转向架的运动几何关系,并推导出了车辆横向偏移量数值与曲线半径、转向架主要几何尺寸之间的几何关系,以及转向架偏转角大小与曲线半径和杜瓦梁长度的关系。可根据设计要求规定的线路半径以及偏移量和偏转角要求,参照本文所推导的关系式对转向架主要几何尺寸进行优化。本文主要考虑磁浮车辆过曲线时离心力和超导体自导向力对转向架曲线通过能力的影响,但在计算时未考虑悬挂力、超高等因素,因而计算值与实际结果存在一定的误差。该结论可作为转向架初步设计及优化的参照依据。

