基于灰色关联与BP神经网络的蒸发量预测模型研究

王 泽

（临汾市水文水资源勘测分局，山西 临汾 041000）

中国国土面积963万km2，现有2 474个国家级地面站，国家级气象站覆盖率较低，且现有气象站数据存在蒸发量缺测现象，正确认识水面蒸发量与气象因子之间的关系，建立适用于中国地区的区域性水面蒸发计算模型，对水资源利用等都具有十分重要的现实意义[1-3]。目前也有学者结合BP（Back-Propagation）神经网络等建立了蒸发量预测模型，但对不同气象因子组合与蒸发量预测结果的影响极为缺乏[4-5]。

以山西省晋城市阳城气象站2015—2016年日气象数据为基础，利用灰色关联理论，计算各影响因子对水面蒸发量的灰色关联度，选择关联度较高的影响因素进行组合，作为模型输入变量组，建立了不同气象因子组合下的蒸发量的BP预测模型，并以该站2017年日气象数据对模型模拟结果进行验证，分析模型的合理性。

1 研究区气象数据

选择晋城市阳城站（站码53 975）基础气象数据，数据来源中国气象科学数据共享服务网，包括2016—2017年阳城站的逐日平均气温（TEM）、逐日平均风速（WIN）、逐日日照时数（SSD）、逐日平均相对湿度(RHU)、逐日20—20时累计降水量（PRE）及逐日蒸发量（EVP）数据。

2 因子关联度与影响因子组合

2.1 灰色关联度排序及输入因子选择

灰色系统理论是学者邓聚龙于1982年创立的预测理论，是一种解决贫信息、少数据问题的常用方法。原理是以样本数据为依据，利用灰色关联理论，求出灰色关联度，以此描述因素间关系的强弱和次序。利用灰色关联理论，确定各气象因子对蒸发量作用的大小，合理确定蒸发量预测模型的输入因子。

2.2 蒸发量BP神经网络预测模型

利用Matlab软件设计模型的BP神经网络结构。所选择的训练函数、输入层激活函数、隐含层激活函数与输出层激活函数分别为trainlm函数、sigmoid函数、tansig正切函数与purelin线性函数。设定的建模参数如表1所示。

表1 模型设定的训练参数

计算时，依据公式（1）限定的最小初始隐含层节点数，构建网络模型。

式中：z——中间隐含层神经元个数；

f——输入层神经元个数；

k——输出层神经元个数；

p——介于0～10的任意常数。

蒸发量BP神经网络预测模型拓扑结构，如公式（2）所示：

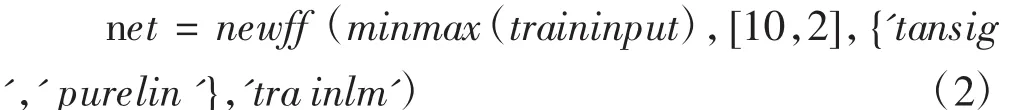
式中：net——蒸发量BP预报模型结构；

newff——Matlab工具箱中的BP神经网络函数；

minmax（）——输入变量的取值矩阵；

traininput——输入变量；

[10，2]——10为中间隐含层个数，2为输出隐含层的个数；

tansig——输入层到隐含层的传递函数；

purelin——隐含层到输出层的传递函数；

trainlm——灰色BP神经网络预报模型的学习函数。

2.3 评定标准

通过比较训练结果，决定系数R2对模型的预测效果，R2越大预测结果越好。评判系数见公式（3）：

式中：N——样本数量；

θi——实测值；

2.4 蒸发量影响因子分析

利用灰色关联理论计算得到影响蒸发量的5个参数对蒸发量的关联度，如表1所示。一般关联度大于等于0.8时，子序列与母序列关联度很好[6]。本次研究选择的参数的关联度均在0.80以上，因此各气象因子的选取是合理的。

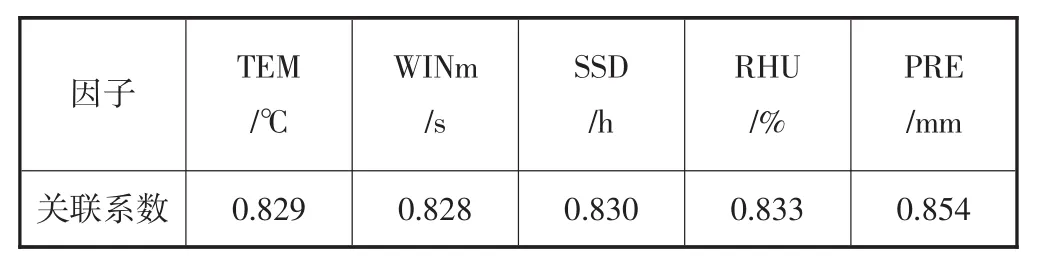
表1 各气象因子与蒸发因子关联度

4 模型的训练精度对比

所选输入因子，有逐日平均气温（TEM）、逐日平均风速（WIN）、逐日日照时数（SSD）、逐日平均相对湿度（RHU）、逐日20—20时累计降水量（PRE）及逐日蒸发量（EVP）。预报模型精度的提高，不仅依赖于数据挖掘技术的应用，还取决于输入变量的选择。为研究不同因子组合下的模型预测效果，分别构建不同数量因子组合下的预测模型，共计26组，对模型输出结果进行检验，从而寻求最佳的模型输入因子组合。以2015—2016年日系列气象因子组合作为输入变量，以2015—2016年日蒸发量作为输出变量，构成模型训练样本，构建BP模型。取训练效果最佳的BP神经网络模型，以2017年相应的气象因子组合，作为所建预测模型的测试样本，得到模型的拟合结果。通过对26种因子组合样本进行训练，建立了26个蒸发量预测模型，各因子组合下的训练效果，如表2所示。

表2 各因子组合下的模拟效果

由表2可知，各因子组合下的模型R2介于0.570与0.929之间，训练差距较大，表明因子组合是影响蒸发量预测精度的关键因素。建立的BP蒸发量训练模型精度最高（R2最大取为0.929）时，对应的因子组合为TEM+WIN+SSD+RHU+PRE；其次R2为0.920时，对应的因子组合为TEM+WIN+SSD+RHU；训练模型精度最低（R2最小为0.570）时，对应的因子组合为RHU+PRE，最佳与最差训练结果对比见图1。

这表明，对晋城地区的蒸发量预测，取TEM+WIN+SSD+RHU+PRE组合，进行BP模型构建与训练，模型模拟结果最为可靠，更为接近实际，TEM+WIN+SSD+SSD+RHU组合次之。取RHU+PRE组合其结果较差，不能为实际提供参考。

图1 训练结果对比图

本文取TEM+WIN+SSD+RHU+PRE组合作为输入因子训练得到的BP神经网络模型对晋城市2017年蒸发量进行预测，结果如图2所示。

图2 预测实测结果对比

得到预测值与实测值的R2为0.629，显著性P为0.000，达到了显著相关水平，以相对误差在20%以内作为判定标准，该预测模型对蒸发练的预测共有231d，合格率为63.11%，可见该模型预测结果与实际情况较为一致。

5 结语

基于灰色关联与BP神经网络，建立了26组由不同因子组合的晋城地区蒸发量预测模型，对模型精度进行对比分析后，得出气象因子组合对模型训练效果具有重大影响。在晋城地区模型模拟精度最高时，对应的因子组合为TEM+WIN+SSD+RHU+PRE，此时训练模型R2值0.929。

本研究内容可为蒸发量预测提供新的思路：实践中当资料无法满足最佳因子组合时，可根据本研究所得的因子组合精度表，选取所能得到的现有因子资料，进行预测精度最高的因子组合，对该地区的蒸发量进行预测。一方面，有助于提高资料充足地区的蒸发量预测精度；另一方面，可以为资料缺乏地区的蒸发量预测提供参考。建议对不同地区的季节性蒸发量预测模型进行研究，寻找区域性最佳预测因子组合，为蒸发量预测提供更多依据。