The Quality Assessment of Non-Integer-Hour Data in GPS Broadcast Ephemerides and Its Impact on the Accuracy of Real-Time Kinematic Positioning Over the South China Sea

Zhangzhen Sun, Tianhe Xu, , Fan Gao, Chunhua Jiang and Guochang Xu

Abstract: Abnormal effects in GPS broadcast ephemerides can have a significant effect on real-time navigation and positioning solutions that use the orbit and clock error data provided by GPS broadcast ephemerides.This paper describes three types of non-integerhour navigation data in GPS broadcast ephemeris data.Compared with GPST integer hour data, we find that there are two types of data blocks for non-integer-hour navigation containing gross errors with different levels of precision, which is reflected in the user range accuracy (URA) of the broadcast ephemeris.These gross errors can cause large deviations when using the GPS broadcast ephemeris for orbit calculation and lead to a decrease in the kinematic positioning accuracy.An improved weighting method which is based on the consistency relationship between the URA value and the orbital precision is proposed to improve the positioning accuracy by controlling the effect of gross errors in the broadcast ephemerides.The correction algorithm proposed in this paper was applied to real-time kinematic positioning with shipborne GPS data over the South China Sea.The results showed that the proposed positioning algorithm can effectively reduce the effects of gross errors in the broadcast ephemeris, and significantly improve the accuracy of the navigation and positioning.

Keywords: GPS broadcast ephemeris, non-integer-hour navigation data, URA, kinematic positioning.

1 Introduction

Real-time kinematic positioning is one of the main modes employed by most navigation users, especially for marine navigation, and it has long been a key research field in the area of global navigation satellite systems (GNSS) [Yi (2011)].At present, there are two widely-adopted GNSS positioning methods for high-precision positioning-absolute positioning and relative positioning.The advantages of relative positioning are its high accuracy and fast positioning.However, its disadvantages for real-time positioning are also obvious.First, relative positioning is difficult to achieve in areas without networks such as the open sea and mountains.Second, the positioning accuracy will decrease with an increase in the distance between two points, and it is impossible to maintain highprecision positioning at all times and in all places.Sometimes it is difficult to obtain high precision from relative positioning on the open sea or in remote areas, as the distance between the rover and the reference station can reach hundreds or even thousands of kilometers.In these scenarios, absolute positioning plays a key role.Absolute positioning can achieve high precision in the specified coordinate system with simplicity, speed and efficiency using only one receiver, and its accuracy is not affected by the reference station receiver.Thus, GNSS absolute positioning is more practical than relative positioning in real-time GNSS positioning applications, such as for vessel monitoring and vehicle navigation.

The accuracy of real-time kinematic positioning has greatly improved as the quality of observation data has improved, and as the number of observation satellites has increased with the development of GNSS.However, decimeter-level or even centimeter-level positioning accuracy is still difficult to achieve.One important reason is that broadcast ephemeris is used in real-time kinematic positioning, and the accuracy of the satellite orbit and clock error is not high.In addition, it is often accompanied by gross errors, which seriously affect the accuracy and reliability of real-time kinematic positioning [Liu and Wang (2014)].

In the past, real-time kinematic positioning was usually carried out by IGS Ultra-rapid (IGU) orbit and clock products, and this requires the network communication to obtain the necessary data.At present, the accuracy of the prediction of the satellite orbit is 5 cm in IGU products when the clock is 3 ns; this represents a range of 0.9 m, and the predicted clock errors will increase with time [Nie, Gao, Wang et al.(2018)].To make it easier to access real-time navigation and positioning, the international GNSS service (IGS) has been providing an open-access real-time service (RTS) since 2013, with an accuracy of about 5 cm in the RTS orbit, and of about 0.1-0.15 ns for the clock (http://www.igs.org/rts/monitor), which allows RT-PPP users to achieve a high positioning performance.However, it is difficult to obtain real-time service products for areas without network coverage, and thus the receiver must resolve location information with no outside information.In this situation, the accuracy of the broadcast ephemeris data received in real time has a direct impact on the positioning result.In recent years, the accuracy of broadcast ephemerides has been greatly improved due to new satellite launches, an increased number of ground control stations, and improvements in the prediction algorithms for satellite orbits and clock errors.The accuracy of broadcast ephemerides is now better than 1 m [Tao, Shi and Guo (2015); Noureldin, Karamat and Georgy (2013)].In studying the effect of broadcast ephemeris on real-time kinematic positioning, most current studies focus on an accuracy analysis of the broadcast ephemeris.As we know, the general broadcast ephemeris data block is updated every two hours; i.e., at 0, 2,···, 22.However, non-integer-hour time data blocks often appear in the navigation data as a result of abnormalities in the navigation satellite and the ground control station firmware [Heng and Gao (2010)].These non-integer-hour time data blocks appear in the broadcast ephemeris on 16*Ns (N=1, 2, 3, ···, 15) before the integer time, and the accuracy is often better than conventional broadcast ephemerides (data blocks at times 0, 2,···, 22) [Tao, Shi and Guo (2015)].However, other non-integer time broadcast ephemeris data blocks have been found in the broadcast ephemerides of most satellites recently.These non-integer time data blocks are irregular, and generally appear in the first half of the hour.The orbit accuracy calculated with these data is inconsistent and poor compared with the integral time data blocks, and seriously affect the positioning accuracy.The presence of these non-integer-hour time data blocks can be determined from the user range accuracy (URA) in the broadcast ephemeris.The URA is a statistical indicator of the ranging accuracies with a specific space vehicle (SV), and it is a onesigma estimate of the user range errors in the navigation data for the transmitting satellite.It includes all errors for which the space and control segments (SCSs) are responsible, but does not include any errors introduced in the user set or the transmission media [Tokura, Yamada, Nobuaki et al.(2004)].

This paper first describes the types of non-integer-hour data blocks in GPS broadcast ephemeris in detail, and analyzes the quality of the non-integer-hour and integer-hour data in the broadcast ephemeris.Next, it solves the real-time kinematic positioning of GPS observation data in the open sea based on these non-integer-hour time data blocks in the broadcast ephemeris, and analyzes the effect of gross errors in the non-integer-hour data on the real-time kinematic positioning of seaborne ships.Last, it proposes a kinematic positioning strategy for when an abnormal data block appears in the broadcast ephemeris.Some recommendations are also provided on how to use GPS non-integerhour data blocks.

2 The GPS non-integer-hour data blocks

2.1 The statistics of abnormal data block information

In GPS positioning, the quality of the broadcast ephemeris is the main factor that affects the positioning results directly.Gross errors and abnormal data in the broadcast ephemeris will lead to low accuracy for the satellite orbits and clock errors, resulting in the wrong position and confusing navigation in extreme cases.These abnormal data may be caused by firmware anomalies in the GPS satellites and ground control stations or incorrect prediction data, and data block loss and redundancy in the navigation ephemeris.The types of non-integer-hour data blocks also create anomalies in the broadcast ephemeris [Heng and Gao (2010)].The types of non-integer-hour data blocks used in navigation are shown in Tab.1.Type A1 is a non-integer-hour time data block at 16 N×s before the integer time, type A2 is a non-integer-hour time data block on 25 min of odd integer time, and type A3 is a noninteger-hour time data block on 30 min of odd integer time.A1 can be divided into two types: one contains only a non-integer-hour time data block on 16 N×s before the integer time, and the other contains both a non-integer-hour time data block on 16 N×s before integer time and an integer-hour time data block.Some research has shown that the accuracy of the satellite orbits and clock solved by that data is equal to or better than the accuracy of the satellite orbits and clock solved by an integer time data block, and this can be verified from the URA of the broadcast ephemeris [Tao, Shi and Guo (2015)].Tab.2 shows non-integer-hour time data blocks appearing on 16 N×s before integer time.

Table 2: Non-integer-hour time data block on 16N×s before the integer time

Table 3: Non-integer-hour time data block on 25 min of the odd integer time

Data containing anomalous non-integer-hour time data blocks on 25 min of the odd integer time do not appear many times in one day, and are only included in the data from some satellites.It is worth noting that integer-hour time data blocks or non-integer-hour time data blocks on 16N×s before the integer time will be given normally when such data appears.The appearance of such broadcast data blocks will have an impact on the real-time kinematic positioning for the rest of time until the next integer-hour time data block appears.If the orbit error calculated by this navigation data block is very large, this will significantly reduce the positioning accuracy.Tab.3 shows two kinds of non-integerhour time data blocks: A2-1 (contains non-integer-hour time data blocks on 16 N×s before the integer time and data on 25 min of the odd integer time) and A2-2 (contains non-integer-hour time data blocks on 16 N×s before the integer time, integer-hour time data blocks and data on 25 min of the odd integer time).Data containing anomalous non-integer-hour time data blocks on 30 min of the odd integer time appear many times in one day, and are included in the data from most satellites.The integer-hour time data block or the non-integer-hour time data block on 16 N×s before the integer time will be given normally when such data appears.The three types are shown in Tab.4: A3-1 (contains non-integer-hour time data blocks on 16N×s before the integer time and data on 30 min of the odd integer time), A3-2 (contains non-integer-hour time data blocks on 16N×s before the integer time, integerhour time data blocks and data on 30 min of the odd integer time) and A3-3 (contains non-integer-hour time data blocks on 16N×s before the integer time, integer-hour time data blocks and data on 25 and 30 min of the odd integer time).

Table 4: Non-integer-hour time data block on 30 min of the odd integer time

In conclusion, the broadcast ephemeris contains different types of data blocks, including the conventional broadcast ephemeris (data blocks on time 0, 2,···, 22) and non-integer time broadcast ephemeris data blocks, including the 16 Ns×data blocks, which appear 16 Ns×before the integer time.The reason for broadcasting data on 25 min and 30 min is to avoid the status of the lack of observations just caused by the elimination of available satellites with gross error in integer time broadcast ephemeris, especially for the real-time positioning.

2.2 User range accuracy

Whether the GPS orbit calculated by the broadcast ephemeris is available for positioning or not when anomalous data blocks are appearing can be initially determined from the URA of the broadcast ephemeris.URA is a statistical indicator of the ranging accuracies obtainable with a specific SV.URA is a one-sigma estimate of the user range errors in the navigation data for the transmitting satellite, and it includes all errors for which the SCSs are responsible.It does not include any errors introduced in the user set or the transmission media.The URA values are generally within the specified interval, and the URA index (N) is an integer in the range 0 to 15 and has the following relationship to the URA of the SV, as shown in Tab.5.

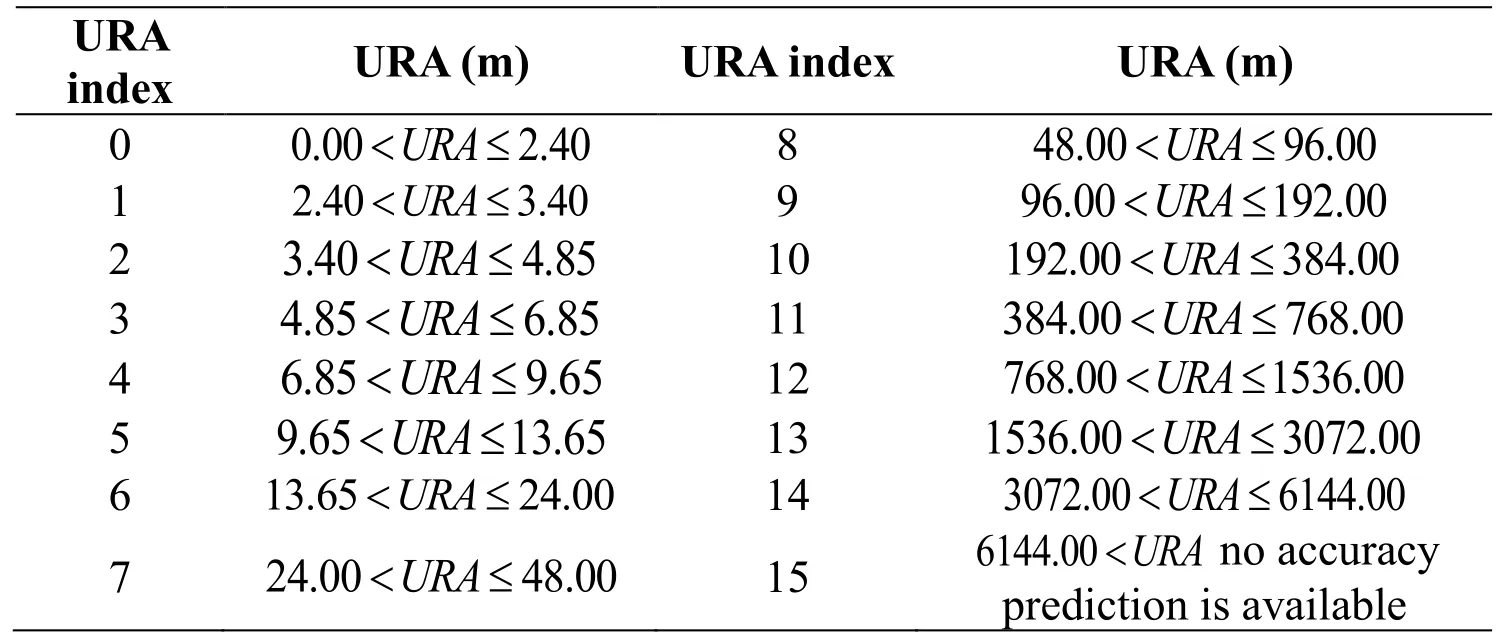
Table 5: The relationship between URA and index (N)

For each URA index (N), users may compute a nominal URA value (X) given by:

·If the value of N is 6 or less,,

·If the value of N is 6 or more, but less than 15,,

·N=15 shall indicate the absence of an accuracy prediction and shall advise the unauthorized user to use that SV at his own risk.

For N=1,3,5, X should be rounded to 2.8, 5.7, and 11.3 meters, respectively.

3 The analysis of abnormal data of in GPS broadcast

3.1 Data description

In GPS positioning, the quality of the broadcast ephemeris affects the positioning result directly.Gross errors and abnormal data in the broadcast ephemeris will lead to low accuracy for the satellite orbits and clock errors, resulting in the wrong position and confusing navigation in extreme cases.To assess the quality of the broadcast ephemeris when anomalous data appear, the GPS broadcast data for DOY 168-174 in 2018 was selected for analysis.The marine shipborne GPS data used in this test were provided by the Second Institute of Oceanography in the South China Sea.There is only one GPS receiver, Trimble 5700, which has a sampling rate of 1 s.Tab.6 shows statistics on abnormal data blocks in the GPS broadcast.In Tab.6, T is the total number of data blocks broadcast in one day.A1, A2 and A3 are the types of non-integer-hour time data blocks.Tab.6 shows that the percentage of all types of abnormal data in the overall ephemeris data can reach 46%, and the probability of abnormal data is very high.According to one study [Noureldin, Karamat and Georgy (2013)], the accuracy of orbit calculated by a type A1 broadcast data block is equal to or higher than the accuracy calculated by the integer-hour time data block, and this is also verified by the URA value for type A1 data.Fig.1 shows the value of the URA for different GPS broadcast times.The figure shows that the URA for type A1 data is approximately equal to that for a data block on the integer-hour time, or even slightly lower.This supports the assertion that the accuracy of orbit calculated by type A1 data is higher than that calculated by the data block on the integer-hour time.As a result, we do not analyze type A1 data in this paper.

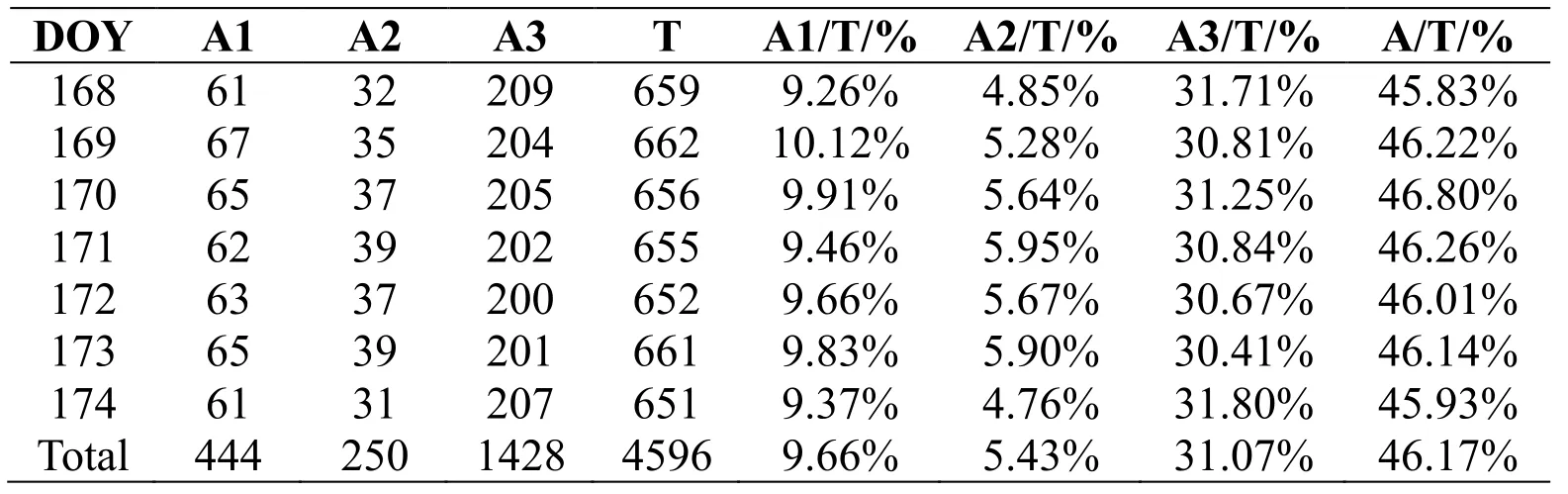
Table 6: Statistics on abnormal data blocks in the GPS broadcast

Figure 1: The statistics of the URA for different GPS broadcast times

Fig.1 shows that the value of the URA for abnormal data types A2 and A3 is larger than for the integer data, with type A2 data being more accurate than type A3 data; the accuracy is also poor.For users of real-time kinematic positioning, it is important to study how to reduce the effect for positioning and optimize the geometry of space satellites when abnormal data appears, because the previous ephemeris data are not stored, and the abnormal ephemeris data are not evaluated.In this paper, two types of noninteger-hour time data block are studied and the characteristics of these two types of data are analyzed.In addition, the positioning algorithm is optimized for real-time received ephemeris data to enable use of all the satellite data without affecting the accuracy of the real-time kinematic positioning.

3.2 Comparison of orbits at different times

In this paper, the broadcast ephemeris data are divided into A2, A3 and integer-hour time data blocks to verify the consistency of the URA and the accuracy of orbit calculated from the broadcast ephemeris, and to compare with the final precise ephemeris data generated by the IGS.The accuracy of orbit calculated by different type is evaluated.The algorithm of the orbit calculate is no longer stated here, which has been described in many studies.In addition, to remove the error caused by orbit interpolation, the interval in the orbit position calculated from the broadcast ephemeris is 15 min, which is the same as the orbit coordinates given by the precise IGS ephemeris.The accuracy of the GPS broadcast for different types of data is shown in Figs.2, 3 and 4.

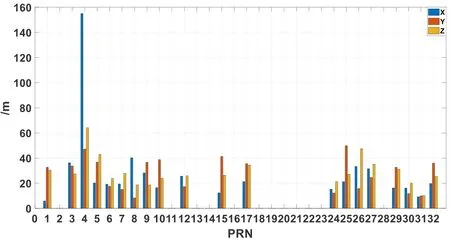
Figure 2: Accuracy of the GPS broadcast orbit at time 25 min

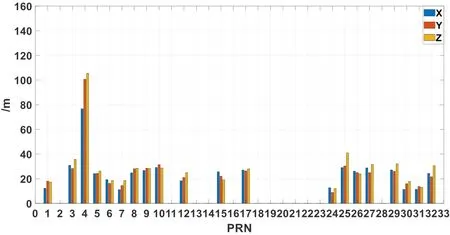
Fi gure 3: Accuracy of the GPS broadcast orbit at time 30 min

Figure 4: Accuracy of the GPS broadcast orbit at integer time

We can see from the Fig.2 to Fig.4 that non-integer-hour time data blocks types A2 and A3 are concentrated in some satellites, and the error in the satellite position calculated from them is one order of magnitude larger than the error calculated from the integerhour data block.The accuracy of orbit calculated from different broadcast ephemeris types shows a positive correlation with the URA; that is to say, if the URA in the realtime broadcast ephemeris received by the user is large, the orbit accuracy calculated from the broadcast ephemeris is low.This also shows that the URA value can be used to assess the accuracy of the broadcast ephemeris.

In real-time kinematic positioning, the time during which the positioning affected by noninteger-hour time data blocks in the broadcast ephemeris is from a non-integer-hour time data block to the next integer-hour time.Therefore, the statistics of the accuracy of the data between the non-integer-hour time points to next integer-hour time point, which can better reflect the effect of the non-integer-hour time data block.The following figure shows the accuracy of orbit calculated from the broadcast ephemeris for types A2 and A3.

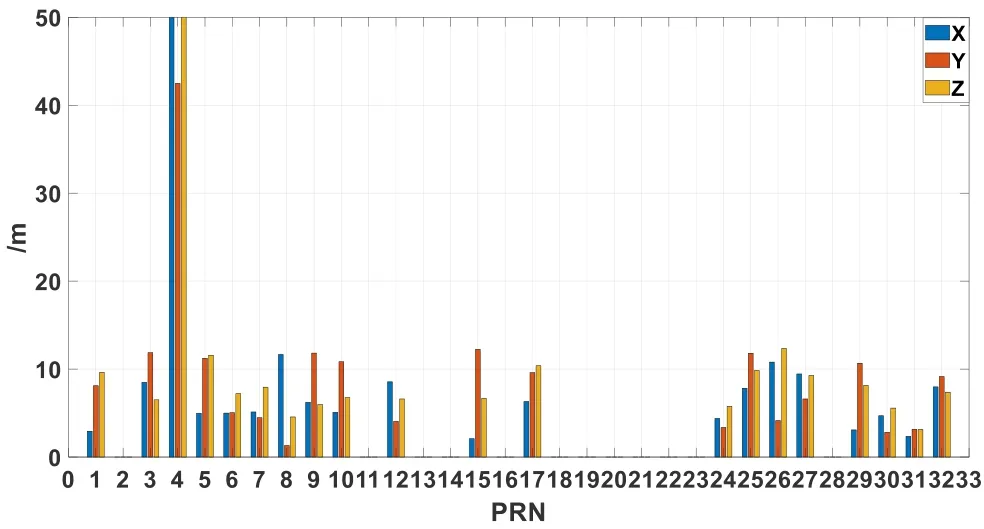
Figure 5: Accuracy of the GPS broadcast orbit between 25 min and the next integer time

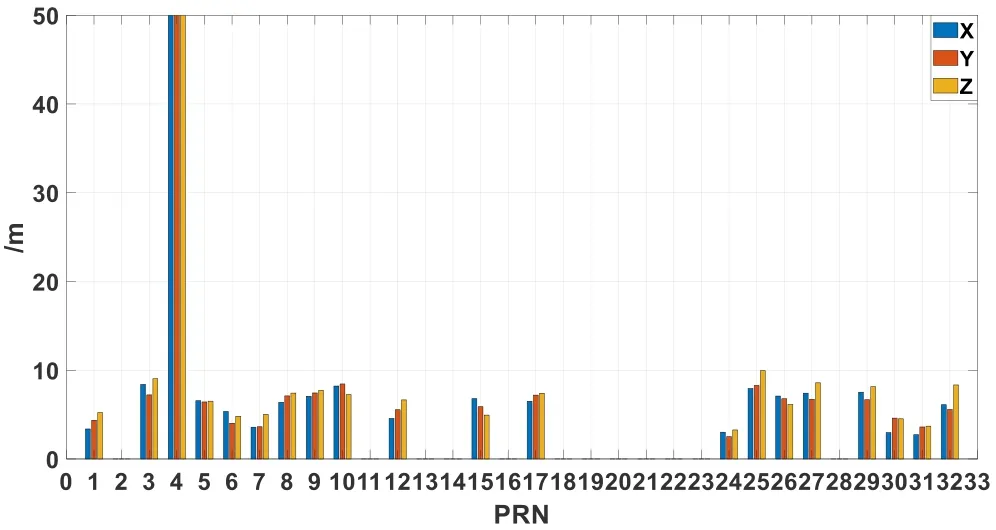
Figure 6: Accuracy of the GPS broadcast orbit between 30 min and the next integer time

Fig.5 and Fig.6 show that the accuracy of the GPS broadcast orbit between the noninteger-hour time and the next integer time is generally 5-10 meters.However, the above is only a matter of the statistical value of orbit accuracy.Sometimes, the bias of orbit extrapolated from the non-integer-hour time data block may be very large, and using that data at these moments will therefore have an impact on the accuracy of real-time kinematic positioning.

Table 7: Orbit statistics calculated from different GPS broadcast data types

Tab.7 shows that the accuracy of orbit calculated from type A3 data is higher than for type A2 data, and this does not match the above-mentioned.The accuracy of orbit calculated from the broadcast ephemeris shows a positive correlation with the URA.The reason is that the type A2 data has been extrapolated for 35 min up to the next integer hour point, but the type A3 data has only been extrapolated for 30 min.Although this may affect the statistical accuracy, it does not affect the fact that the orbit error for the two types of data is large.Here, we will focus on the impact of the two types of broadcast ephemeris data on real-time kinematic positioning, and will not discuss the degree of agreement between the two types of broadcast errors and the URA.

4 Real-time kinematic positioning with broadcast

In navigation and positioning on the open seas, Xu et al.discussed the GPS Precise Point Positioning (PPP) model and data processing method and achieved sub-meter-level realtime kinematic positioning at sea [Xu and Chen (2014)].Chai et al.adopted algorithms for combined BDS and GPS pseudorange differential positioning and BDS triplefrequency network RTK and achieved meter-level navigation and centimeter-level positioning services on the open seas [Chai and Huang (2016)].Wang et al.have achieved a better than 0.8 m positioning accuracy in the planar direction and a better than 2 m positioning accuracy in the elevation direction by obtaining corrections to the precision orbit and clock errors and ionospheric grid for GNSS satellites which were broadcast by IGS through the network [Wang, Zheng and Yu (2017)].Gao et al.[Gao, Gao, Pan et al.(2015)] proposed a real-time PPP method based on regional continuous operation reference stations (CORS) for ocean application, and real-time PPP experiments in remote areas were carried out to simulate ocean applications based on the predicted IGU orbit and clock products.And it has achieved a positioning error in the three directions (North/East/Up) are within 6 cm after 1-hour filtering convergence and provided a new possible strategy for oceanic positioning application.In the monitoring of remote marine platforms, Beidou communication has played an important role.BDStar Navigation Co.Ltd.(China) has done detailed research into real-time communication and positioning products based on the Beidou short message service.

However, the above-mentioned ocean kinematic positioning research is based on quasireal-time, simulated real-time or external correction data.To truly realize real-time kinematic positioning on the open seas, further studies into the theory and algorithm of kinematic positioning using only the received broadcast ephemeris data must be conducted.

4.1 Methods and model

The un-differenced ionospheric-free model is generally used in positioning.Therefore, many errors in the positioning process are corrected by empirical models.Unlike in the relative positioning method, navigation positioning cannot eliminate system errors and the positioning accuracy in navigation is closely related to the observation quality, orbit and clock error.This is particularly serious when positioning using broadcast ephemeris.The linearized equations of the original pseudorange and carrier phase observation of the ionospheric-free model are as follows.

Kinematic positioning with the ionospheric-free model considers the high-order term in the ionospheric delay to have little effect on the result, and ignores them.The hardware delay parameter is considered to be absorbed by the ambiguity parameter, and the ambiguity finally adopts the float solution.Both the satellite orbit position and clock error are calculated from the broadcasting ephemeris using Eqs.(1) and (2).The tropospheric delay is corrected by the Saastamoinen model.The linearized equations can be written as follows:

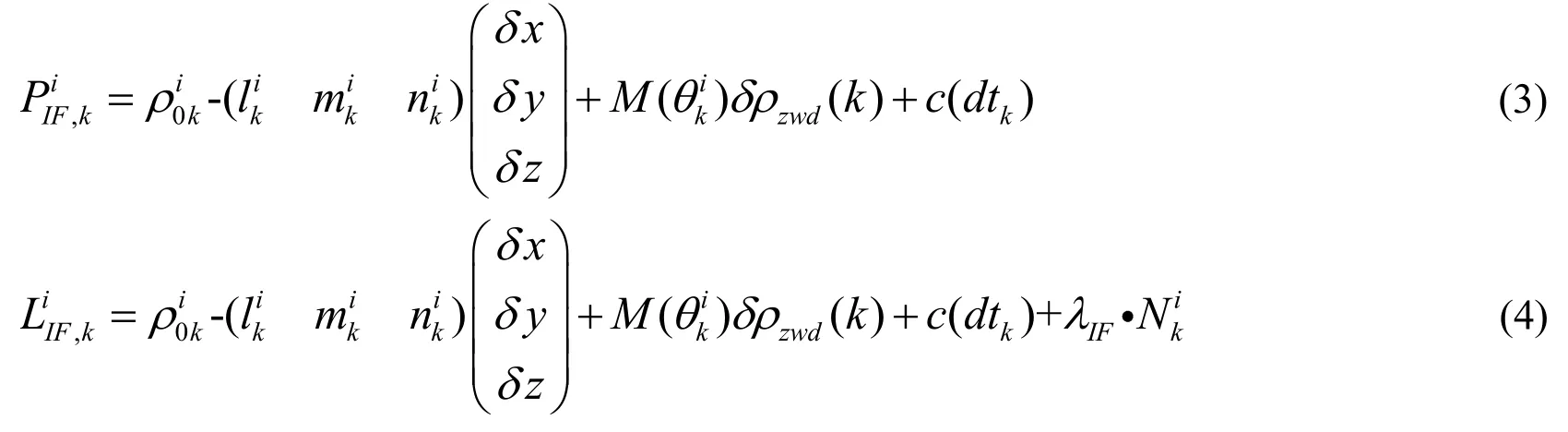
The error equation can be expressed as:

where,

In GNSS navigation positioning, classical least squares theory is usually adopted for parameter estimation.Least squares estimation has the ability to balance the errors, but it has no ability to eliminate or weaken gross errors [Yang (2006); Zhang, Zhang and Yue (2015)].Any abnormal errors or small gross errors in the observation data or satellite ephemeris will cause the solution to deviate significantly and reduce the positioning accuracy.To ensure high navigation positioning accuracy, a robust least squares algorithm is one of the best estimation algorithms to control the influence of abnormal data.

The number of satellite observations was limited, because the receiver used in this paper could only receive GPS signals in kinematic positioning and navigation.To avoid the status of the lack of observations caused by the elimination of satellites, the non-integerhour time data block was also used, although it contains gross errors such as those related to type A2 and A3 data blocks.Therefore, we designed a robust theoretical algorithm to effectively reduce the influence of the gross error on the non-integer-hour time.To deal with this and with the relationship between the accuracy of the broadcast ephemeris orbit and the URA value, in processing the positioning, we set different weights according to the URA of the satellites and reduced the positioning deviation caused by poor precision to guarantee reliability of positioning.The basis is similar to the theory of robust estimation, but with the following method used to define the weights.

where Nis the URA index, andis the diagonal value of weight matrix.Processing of the parameter solution was performed in accordance with forward Kalman filtering.

4.2 Kinematic positioning in marine environments

The marine shipborne GPS data used in this test was provided by the Second Institute of Oceanography in the South China Sea.The GPS receiver was a Trimble 5700, and the observation data contained the pseudorange and carrier-phase observations on frequencies L1 and L2 with a sampling rate of 1 s.Observations were carried out on DOY 168 to 174 in 2018 in the South China Sea region to verify the real-time kinematic positioning algorithm based on the broadcast ephemeris data blocks.Fig.7 shows the trajectory of the vessel platform in the South China Sea.

Figure 7: Trajectory of the vessel platform

We can see from Fig.7 that the test region was remote from the mainland.As a result, it was not possible to use real-time differential positioning because the receiver could not obtain data from other stations over the network.Therefore, high precision differential positioning was not possible.

Because the GPS receiver used in this test was a lower version and had suffered minor damage, we found that the received data were poor in quality and was often interrupted.This reflects the current use status of most receivers on the market.Fig.8 shows the changes in the total number of GPS satellites on DOY 168.

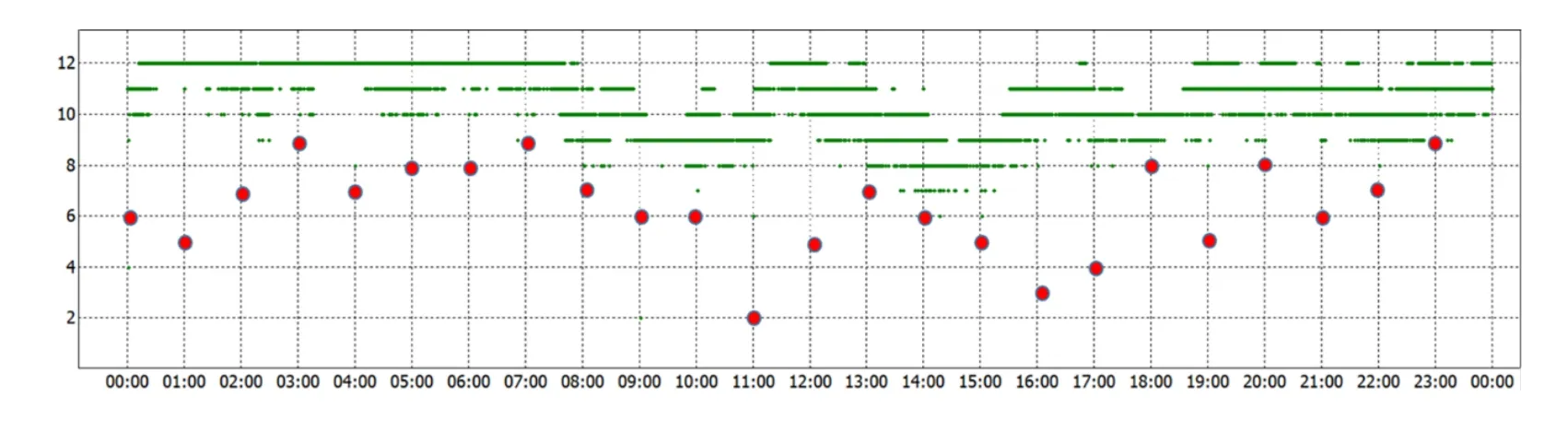
Figure 8: Total number of GPS satellites in DOY 168

Fig.8 shows that the GPS receiver recaptured the signal almost every hour, until the number of GPS satellites declined sharply and it was no longer possible to determine the position.This made real-time kinematic positioning difficult, and the lack of a reasonable data processing strategy significantly affected the positioning result.

To test the positioning quality and accuracy of real-time kinematic positioning when using broadcast ephemerides, the final orbit and clock error products from IGS were also used as reference values to evaluate the accuracy.The high-precision positioning software system compiled by Shandong University was used in the test and for reference value acquisition.The positioning results using the existing positioning algorithm are shown in Fig.9 and Fig.10.

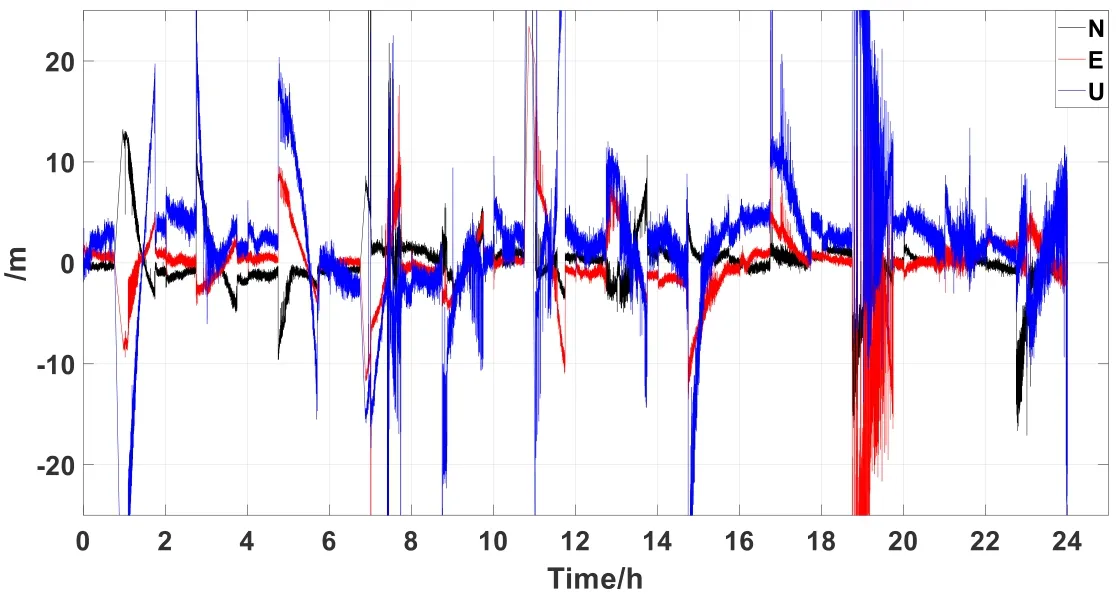
Figure 9: Difference between the positioning results based on the existing positioning algorithm and the reference value in DOY 168

Figure 10: Positioning accuracy statistics for seven days based on the existing positioning algorithm

Fig.9 shows the positioning deviation of DOY 168 data based on the broadcast ephemeris, and the non-integer-hour time data block is not considered in here.It can be seen in Fig.9 that the error increased abnormally around 19:00 hours.To find a reason for this, we looked at the original observation data at this time.Satellites G10, G12, G14, G15, G20, G21, G24, G25, G29 and G31 could be observed, but satellites G10, G12, G15, G24, G25 and G31 were broadcasting non-integer-hour time ephemeris data blocks, and nearly half of these satellites have problems with large errors in their ephemeris data, resulting in large deviations in the positioning results.Because the results for the other six days were similar to DOY 168, the figures are not given here for reasons of space.

As can be seen from the figure, the positioning deviation is large when non-integer-hour time data blocks exist in the broadcast ephemeris, significantly affecting the positioning results.Another possible reason is the quality of the observed data.The GPS receiver recaptures the signal every hour, and this will be explored later in the data analysis to verify whether this is the cause.Fig.10 shows the positioning accuracy statistics for seven days.The figure shows that the positioning accuracy is up to 10 meters in the three directions, which also indicates that the non-integer-hour time data blocks in the broadcast ephemeris introduced large and non-negligible errors to the kinematic positioning.To obtain better positioning results, these large errors caused by non-integerhour time data blocks must be eliminated or reduced.

As has been discussed, large deviations in the kinematic positioning are caused by the broadcast ephemerides containing gross errors from type A2 and A3 data blocks, and it is thus important to eliminate or reduce these gross errors caused by non-integer-hour time data blocks.At present, low-cost, single-system or single-frequency receivers are generally used in real-time marine and vehicle positioning for economic reasons.However, the demand for low-cost and high-precision positioning devices is increasing as the requirements for high-precision navigation and high-quality positioning increase with the development of technology.It is therefore important to study how to improve the accuracy of real-time positioning in this scenario.The results shown in Fig.11 and Fig.12 are based on the proposed kinematic positioning algorithm.

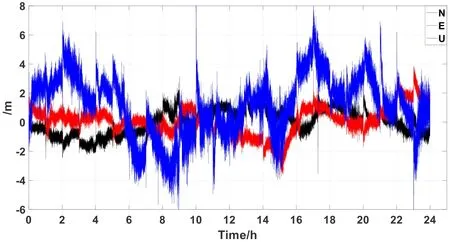
Figure 11: Difference between the positioning results based on the proposed kinematic positioning algorithm and the reference values for DOY 168

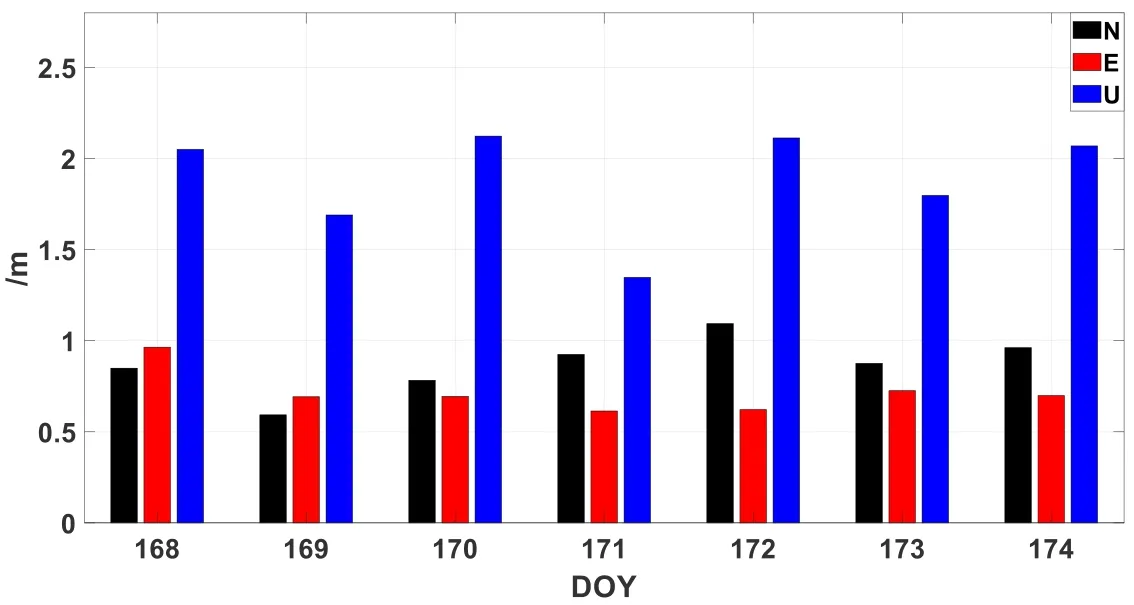
Figure 12: Positioning accuracy statistics for seven days based on the new kinematic positioning algorithm

Fig.11 shows the positioning deviation for DOY 168 data based on the proposed kinematic positioning algorithm, which sets different weights according to the URA of the broadcast ephemeris in real-time kinematic positioning.The figure shows that the weight positioning algorithm can reduce the influence of non-integer-hour time data blocks on kinematic positioning and improve the positioning accuracy.The figure also indicates that signal reacquisition by the receiver does not affect the positioning accuracy in the short term.Fig.12 shows the positioning accuracy statistics for seven days based on the proposed kinematic positioning algorithm, indicating that the positioning accuracy in the three directions can reach the meter level, showing great improvements in kinematic positioning accuracy over the existing algorithm for low-cost receivers.

5 Conclusions

This study analyzed integer-hour and the non-integer-hour data blocks in the GPS broadcast ephemeris, and found abnormal error data in the broadcast data.These abnormal errors can cause large deviations when using GPS broadcast ephemeris for orbit calculations.The orbit accuracy calculated from the broadcast ephemeris correlates well with the URA; this means that the presence of different types of broadcast ephemeris data blocks can be confirmed from the URA.To overcome this problem, an improved weighting method based on the consistency relationship between the URA value and the orbital precision is proposed to improve the accuracy of kinematic positioning when there are abnormal errors in the broadcast ephemeris.This method can improve the accuracy of real-time navigation positioning effectively, and maintain the spatial geometry of the satellite when an abnormal error appears.The proposed algorithm was applied to shipborne GPS kinematic positioning over the South China Sea.The results show that the proposed positioning algorithm can greatly reduce the effect of abnormal errors in broadcast ephemerides on navigation and positioning.

Acknowledgements:The authors would like to thank to Second Institute of Oceanography for the marine GPS data in the South China Sea.And this study is under the support by the National Key Research and Development Program of China (2016YFB0501701 and 2016YFB0501900).National Natural Science Foundation of China (Grant Nos.41574013 and 41874032) and the Funded by the State Key Laboratory of Geo-information Engineering (SKLGIE2016-M-1-1).

References

Chai, J.Z.; Huang, Y.J.(2016): BeiDou coastal differential navigation and precise positioning service system.Hydrographic Surveying and Charting, vol.36, no.3, pp.41-43.

Chen, K.J.; Zamoea, N.; Babeyko, A.Y.; Li, X.X.; Ge, M.R.(2015): Precise positioning of BDS, BDS/GPS: implications for Tsunami early warning in South China Sea.Remote Sensing, vol.7, no.12, pp.15955-15968.

IS-GPS-200(2013).Navstar GPS Space Segment/Navigation User Interfaces.http://www.gps.gov/technical/icwg/IS-GPS-200H.pdf.

Gao, C.F.; Gao, W.; Pan, S.G.; Chen, W.R.; Shi, X.F.et al.(2015): High-precision oceanic real-time positioning application based on regional continuous operation reference stations.Journal of Coastal Research, vol.73, pp.325-330.

Guo, F.; Li, X.X.; Zhang, X.D.; Wang, J.L.(2016): The contribution of Multi-GNSS Experiment (MGEX) to precise point positioning.Advances in Space Research, vol.59, pp.2714-2725.

He, K.F.(2015): GNSS Kinematic Position and Velocity Determination for Airborne Gravimetry (Ph.D.Thesis).Technische Universität Berlin, Germany.

Heng, L.; Gao, X.X.; Walter, T.; Enge, P.(2010): GPS ephemeris error screening and results for 2006-2009.International Technical Meeting of the Institute of Navigation.San Diego, CA.

Kouba, J.; Heroux, P.(2001): Precise point positioning using IGS orbit and clock products.GPS Solutions, vol.5, no.2, pp.12-28.

Li, B.F.; Ge, H.B.; Shen, Y.Z.(2015): Comparison of ionosphere-free, Uofc and uncombined PPP observation models.Acta Geodaetica et Cartographica Sinica, vol.44, no.7, pp.734-740.

Li, X.X; Ge, M.R.; Dai, X.L.; Ren, X.D.; Fritsche, M.et al.(2015): Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo.Journal of Geodesy, vol.89, no.6, pp.607-635.

Liu, Z.Q.; Wang, J.X.(2014): Realization and analysis of real-time precise point positioning based on SSR broadcast ephemeris corrections.Science of Surveying and Mapping, vol.1, no.29, pp.15-19.

Nie, Z.X.; Gao, Y.; Wang, Z.J.; Ji, Y.S.; Yang, H.Z.(2018): An approach to GPS clock prediction for real-time PPP during outages of RTS stream.GPS Solutions, vol.22, pp.1-14.

Noureldin, A.; Karamat, B.; Georgy, J.(2013): Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration.NY: Springer.

Wang, Y.R.; Zheng, Y.G.; Yu, X.(2017): Study on the algorithm of wide area submeter singer point positioning.Journal of Shandong University (Engineering Science), vol.47, pp.1-6.

Xiang, T.; Shi, J.B.; Guo, J.M.(2015): Quality assessment of non-integer-hour data block in GPS broadcast ephemeris.Geomatics and Information Science of Wuhan University, vol.40, no.3, pp.372-378.

Xu, Y.Q.; Chen, R.G.(2014): Research on precise point positioning technology application in engineering practice.Hydrographic Surveying and Charting, vol.34, no.4, pp.66-68.

Yang, Y.X.(2006): Adaptive Navigation and Kinematic Positioning.Surveying and Mapping Peress.

Yi, C.H.(2011): Research on Theory and Application of Real Time Precise Point Positioning (Ph.D.Thesis).Central South University, China.

Zhang, Q.; Zhang, J.Q.; Yue, C.J.(2011): Advanced Theory and Application of Surveying Data.Surveying and Mapping Peress.

Zhang, X.H.; Zuo, X.; Li, P.(2013): Mathematic model and performance comparison between ionosphere-free combined and uncombined precise point positioning.Geomatics and Information Science of Wuhan University, vol.38, no.5, pp.561-565.

Zumbeger, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H.(1997): Precise point positioning for efficient and robust analysis of GPS data from large networks.Journal of Geophysical Research, vol.102, pp.5005-5017.